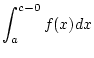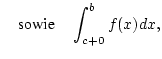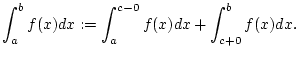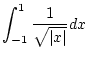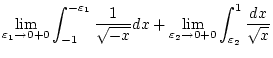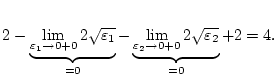Next: Der Cauchysche Hauptwert.
Up: Grundlegende Definitionen
Previous: Einige Beispiele.
Contents
Uneigentliche Integrale treten auch auf, wenn der Integrand 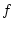 Singularitäten in einem Punkt besitzt. Dazu betrachten wir Funktionen
Singularitäten in einem Punkt besitzt. Dazu betrachten wir Funktionen
![% latex2html id marker 21050
$ f:]a,b]\to \mathbb{K}^{p} $](img82.png) , welche auf jedem Intervall
, welche auf jedem Intervall
![$ [a+\varepsilon ,b] $](img83.png) ,
,
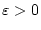 , integrierbar sind.
, integrierbar sind.
Aufgabe 1.1.4.1
Zeigen Sie, daß im Fall
![$ f\in R[a,b] $](img85.png)
gilt
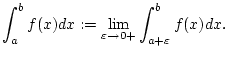 |
(1.1.4.1) |
Ist 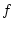 nicht auf dem gesamten Intervall
nicht auf dem gesamten Intervall ![$ [a,b] $](img87.png) integrierbar,
so zieht man die Identität (1.1.4.1) als Definition
eines uneigentlichen Integrales heran:
Analog definiert man das uneigentliche Integral
integrierbar,
so zieht man die Identität (1.1.4.1) als Definition
eines uneigentlichen Integrales heran:
Analog definiert man das uneigentliche Integral
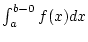 .
.
Oft benutzt man auch einfach die Bezeichnung
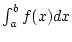 für diese uneigentlichen Integrale; man muß sich aber bewußt sein,
daß es sich dabei für
für diese uneigentlichen Integrale; man muß sich aber bewußt sein,
daß es sich dabei für
![$ f\not \in R[a,b] $](img91.png) nicht um ein
eigentliches Riemann-Integral handelt.
nicht um ein
eigentliches Riemann-Integral handelt.
Besitzt die Funktion
![% latex2html id marker 21081
$ f:[a,c[\cup ]c,b]\to \mathbb{K}^{p} $](img92.png) eine
Singularität in einem Punkt
eine
Singularität in einem Punkt
![$ c\in ]a,b[ $](img93.png) , so kann man obige Definition
wiefolgt modifizieren: Existieren die beiden uneigentlichen Integrale
, so kann man obige Definition
wiefolgt modifizieren: Existieren die beiden uneigentlichen Integrale
unabhängig voneinander, so setzt man
Auch hier handelt es sich für
![$ f\not \in R[a,b] $](img91.png) nicht
um ein eigentliches Riemann-Integral, obwohl die Bezeichnung dies
suggeriert. Gilt hingegen
nicht
um ein eigentliches Riemann-Integral, obwohl die Bezeichnung dies
suggeriert. Gilt hingegen
![$ f\in R[a,b] $](img85.png) , so führt die obige Definition
auf das übliche Riemann-Integral zurück.
, so führt die obige Definition
auf das übliche Riemann-Integral zurück.
Beispiel 1.1.4.2
Wir berechnen das uneigentliche Integral
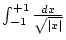
.
Es gilt
Dabei ist es wichtig, dass beide Grenzwerte separat konvergieren,
d.h.
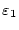
und
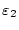
streben unabhängig
voneinander gegen Null. Dies ist im folgenden Beispiel nicht gegeben.




Next: Der Cauchysche Hauptwert.
Up: Grundlegende Definitionen
Previous: Einige Beispiele.
Contents
2003-09-05
![]() Singularitäten in einem Punkt besitzt. Dazu betrachten wir Funktionen
Singularitäten in einem Punkt besitzt. Dazu betrachten wir Funktionen
![]() , welche auf jedem Intervall
, welche auf jedem Intervall
![]() ,
,
![]() , integrierbar sind.
, integrierbar sind.
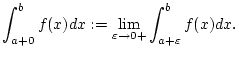
![]() für diese uneigentlichen Integrale; man muß sich aber bewußt sein,
daß es sich dabei für
für diese uneigentlichen Integrale; man muß sich aber bewußt sein,
daß es sich dabei für
![]() nicht um ein
eigentliches Riemann-Integral handelt.
nicht um ein
eigentliches Riemann-Integral handelt.
![]() eine
Singularität in einem Punkt
eine
Singularität in einem Punkt
![]() , so kann man obige Definition
wiefolgt modifizieren: Existieren die beiden uneigentlichen Integrale
, so kann man obige Definition
wiefolgt modifizieren: Existieren die beiden uneigentlichen Integrale