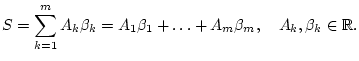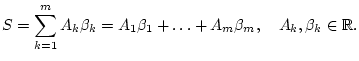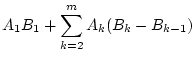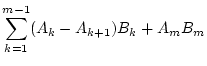Next: Das Abelsche Kriterium.
Up: Konvergenzkriterien für im Allgemeinen
Previous: Konvergenzkriterien für im Allgemeinen
Contents
Wir betrachten Summen vom Typ
Es sei
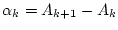 für
für 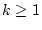 . Dann gilt
. Dann gilt
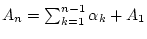 . Wir betrachten außerdem
die Partialsummen
. Wir betrachten außerdem
die Partialsummen
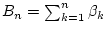 . Wegen
kann man die Summe
. Wegen
kann man die Summe
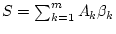 wie folgt
umschreiben:
wie folgt
umschreiben:
Die daraus folgende Formel
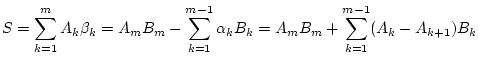 |
(1.7.1.1) |
ähnelt der Formel der partiellen Integration, wenn man die Folge
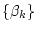 mit
mit 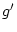 ,
, 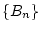 mit
mit 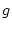 ,
, 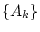 mit
mit
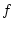 und
und
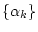 mit
mit 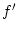 assoziiert.
assoziiert.
2003-09-05