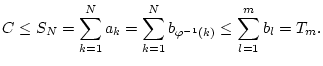Next: Der Riemannsche Umordnungssatz.
Up: Der Umordnungssatz. Summierung über
Previous: Die Monotonität.
Contents
Der folgende Satz sagt aus, daß Konvergenz und Wert einer Reihe aus
nichtnegativen Gliedern nicht von der Anordnung der Summanden abhängt.
 Fall 1: Angenommen, die Reihe
Fall 1: Angenommen, die Reihe
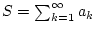 konvergiert. Es sei
konvergiert. Es sei
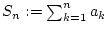 ,
,
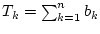 und
und
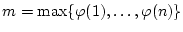 . Dann gilt
Damit ist die Folge
. Dann gilt
Damit ist die Folge 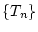 beschränkt. Aufgrund der Monotonität
besitzt diese Folge einen Grenzwert
beschränkt. Aufgrund der Monotonität
besitzt diese Folge einen Grenzwert
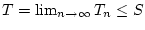 ,
d.h.
Umgekehrt betrachten wir
,
d.h.
Umgekehrt betrachten wir
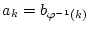 und erhalten
auf gleichem Wege
und erhalten
auf gleichem Wege 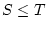 . Daraus folgt (1.3.2.1).
. Daraus folgt (1.3.2.1).
Fall 2 :Angenommen, die Reihe
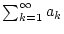 divergiert, d.h.
divergiert, d.h.
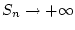 . Damit existiert für jedes
gegebene
. Damit existiert für jedes
gegebene 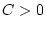 ein
ein
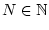 mit
mit
Es sei
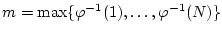 .
Dann gilt
Also divergiert auch die Folge
.
Dann gilt
Also divergiert auch die Folge 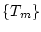 und damit die Reihe
und damit die Reihe
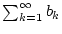 .
.





Next: Der Riemannsche Umordnungssatz.
Up: Der Umordnungssatz. Summierung über
Previous: Die Monotonität.
Contents
2003-09-05
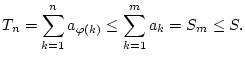
![]() divergiert, d.h.
divergiert, d.h.
![]() . Damit existiert für jedes
gegebene
. Damit existiert für jedes
gegebene ![]() ein
ein
![]() mit
mit