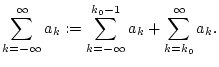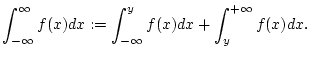Reihen über $\mathbb{Z}\protect$ und uneigentliche Integrale auf $\mathbb{R}\protect$.

Es sei $a_{.}:\mathbb{Z}\to \mathbb{K}^{p}$ eine Folge von Gliedern $a_{k}\in \mathbb{K}^{p}$ mit ganzzahligem Index $k\in \mathbb{Z}$.

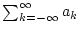
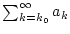
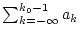
Definition 1.1.2.1   Die Reihe $\sum _{k=-\infty }^{\infty }a_{k}$ nennt man genau dann konvergent, wenn für gewisses $k_{0}\in \mathbb{Z}$ beide Reihen $\sum _{k=k_{0}}^{\infty }a_{k}$ und $\sum _{k=-\infty }^{k_{0}-1}a_{k}$ konvergieren. Man setzt dann

$$\sum _{k=-\infty }^{\infty }a_{k}:=\sum _{k=-\infty }^{k_{0}-1}a_{k}+\sum _{k=k_{0}}^{\infty }a_{k}.$$

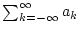
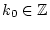
Aufgabe 1.1.2.2   Zeigen Sie, daß die Konvergenz und der Wert von $\sum _{k=-\infty }^{\infty }a_{k}$ unabhängig von der konkreten Wahl von $k_{0}\in \mathbb{Z}$ sind!

Wir betrachten nun eine Funktion $f:\mathbb{R}\to \mathbb{K}^{p}$, welche auf jedem endlichen Intervall intergrierbar ist.

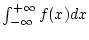
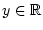
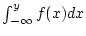
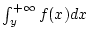
Definition 1.1.2.3   Das uneigentliche Integral $\int _{-\infty }^{+\infty }f(x)dx$ nennt man genau dann konvergent, wenn für gewisses $y\in \mathbb{R}$ beide uneigentlichen Integrale $\int _{-\infty }^{y}f(x)dx$ und $\int _{y}^{+\infty }f(x)dx$ konvergieren. Man setzt dann

$$\int _{-\infty }^{\infty }f(x)dx:=\int _{-\infty }^{y}f(x)dx+\int _{y}^{+\infty }f(x)dx.$$

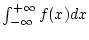
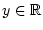
Aufgabe 1.1.2.4   Zeigen Sie, daß in dieser Definition Konvergenz und Wert des uneigentlichen Integrales $\int _{-\infty }^{+\infty }f(x)dx$ unabhängig von der Wahl von $y\in \mathbb{R}$ ist!