Allgemeine Reihen mit nichtnegativen Gliedern

Wir wenden uns jetzt wieder den Eigenschaften von Reihen mit nichtnegativen Gliedern und insbesondere den Anwendungen von Satz 1.3.2.1 zu.

Es sei $A$ eine abzählbare Menge ( $\mbox {card}(A)=\aleph _{0}$) und $a$ eine Abbildung $a:A\to [0,+\infty [$. Wir schreiben $a_{\alpha }=a(\alpha )$ für $\alpha \in A$.

Definition 1.3.4.1   Es sei $\varphi :A\to \mathbb{N}$ eine Bijektion zwischen $A$ und $\mathbb{N}$. Wir sagen, die Reihe $\sum _{\alpha \in A}a_{\alpha }$ konvergiert genau dann, wenn die Reihe $\sum _{k=1}^{\infty }a_{\varphi ^{-1}(k)}$ konvergiert und setzen

$$\sum _{\alpha \in A}a_{\alpha }:=\sum _{k=1}^{\infty }a_{\varphi ^{-1}(k)}.$$

Diese Definition ist nach dem Umordnungssatz unabhängig von der Wahl der konkreten Bijektion $\varphi :A\to \mathbb{N}$. Tatsächlich, es sei $\psi :A\to \mathbb{N}$ eine weitere Bijektion. Dann ist auch $\gamma =\varphi ^{-1}\circ \psi :\mathbb{N}\to \mathbb{N}$ eine bijektive Abbildung auf $\mathbb{N}$ und nach Satz 1.3.2.1 gilt

$$\sum _{k=1}^{\infty }a_{\psi ^{-1}(... ...nfty }a_{\varphi ^{-1}(k)},\quad b_{k}=a_{\psi ^{-1}(k)},\quad k\in \mathbb{N}.$$

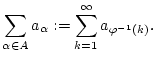
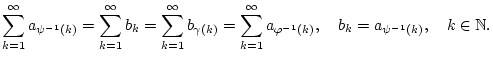
Auf einem analogen Argument basiert der verallgemeinerte Umordnungssatz:

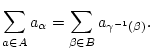
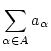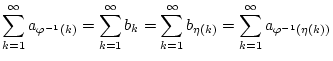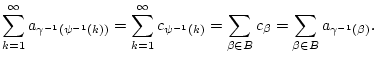Satz 1.3.4.2   Es seien $A$, $B$ zwei abzählbare Mengen und $\gamma :A\to B$ eine Bijektion. Für $a:A\to \mathbb{R}$ mit $a_{\alpha }=a(\alpha )\geq 0$, $\alpha \in A$, konvergiert die Reihe $\sum _{\alpha \in A}a_{\alpha }$ genau dann, wenn die Reihe $\sum _{\beta \in B}\, a_{\gamma ^{-1}(\beta )}$ konvergiert. Dabei gilt

$$\sum _{a\in A}a_{\alpha }=\sum _{\beta \in B}a_{\gamma ^{-1}(\beta )}.$$

$\blacktriangleright$ Wir setzen $b_{k}=a_{\varphi ^{-1}(k)}$, $k\in \mathbb{N}$ und $c_{\beta }=a_{\gamma ^{-1}(\beta )}$ für $\beta \in B$. Es seien $\varphi :A\to \mathbb{N}$ und $\psi :B\to \mathbb{N}$ bijektive Abbildungen. Dann ist $\eta =\phi \circ \gamma ^{-1}\circ \psi ^{-1}:\mathbb{N}\to \mathbb{N}$ eine Bijektion und nach Satz 1.3.2.1 gilt

$$\sum _{\alpha \in A}a_{\alpha } = \sum _{k=1}^{\infty }a_{\varphi ^{-1}(k)}=\sum _{k=1}^{\infty }b_... ...m _{k=1}^{\infty }b_{\eta (k)}=\sum _{k=1}^{\infty }a_{\varphi ^{-1}(\eta (k))}$$

$$= \sum _{k=1}^{\infty }a_{\gamma ^{-1}(\psi ^{-1}(k))}=\sum _{k=1}^... ...(k)}=\sum _{\beta \in B}c_{\beta }=\sum _{\beta \in B}a_{\gamma ^{-1}(\beta )}.$$

$\blacktriangleleft$