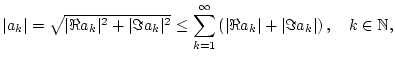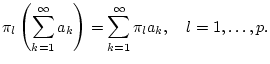Next: Der Umordnungssatz für absolut
Up: Absolute und bedingte Konvergenz
Previous: Zum Zusammenhang zwischen absoluter
Contents
Satz 1.6.3.1
Es sei
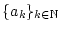 eine Folge nichtnegativer Zahlen und
eine Folge nichtnegativer Zahlen und
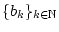 eine Folge von Elementen aus
eine Folge von Elementen aus
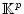 . Angenommen die
Reihe
. Angenommen die
Reihe
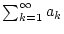 konvergiert und es gilt
konvergiert und es gilt
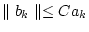 für alle
für alle
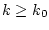 . Dann konvergiert die Reihe
. Dann konvergiert die Reihe
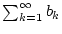 absolut.
absolut.
 Wie im Beweis von Satz 1.6.2.1 folgt die Aussage aus
dem Cauchy-Kriterium und der Ungleichung
Wie im Beweis von Satz 1.6.2.1 folgt die Aussage aus
dem Cauchy-Kriterium und der Ungleichung

Aufgabe 1.6.3.2
Formulieren und beweisen Sie die analoge Aussage für uneigentliche
Integrale.
 Angenommen die Reihe
Angenommen die Reihe
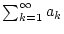 konvergiert
absolut Wegen
konvergiert
absolut Wegen
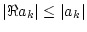 und
und
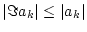 für
für
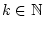 konvergieren nach Satz 1.6.3.1
die Reihen der Real- und der Imaginärteile absolut.
konvergieren nach Satz 1.6.3.1
die Reihen der Real- und der Imaginärteile absolut.
Umgekehrt folgt aus der absoluten Konvergenz der Reihen
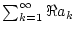 und
und
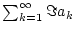 wegen Satz 1.2.3.1
die Konvergenz von
wegen Satz 1.2.3.1
die Konvergenz von
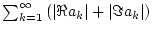 .
Da
.
Da
so konvergiert nach Satz 1.6.3.1 die Reihe
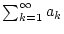 absolut. Die Gleichung (1.6.3.1) folgt nun aus Satz
1.2.3.1.
absolut. Die Gleichung (1.6.3.1) folgt nun aus Satz
1.2.3.1.

Aufgabe 1.6.3.5
Beweisen Sie diesen Satz selbständig!
Satz 1.6.3.6
Es sei
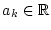 ,
,
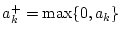 ,
,
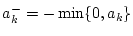 ,
,
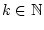 . Die Reihe
. Die Reihe
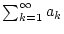 konvergiert genau dann absolut, wenn die beiden Reihen
konvergiert genau dann absolut, wenn die beiden Reihen
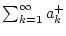 und
und
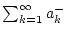 konvergieren.
konvergieren.
 Es gilt
Die Aussage folgt damit direkt aus Satz 1.6.3.1.
Es gilt
Die Aussage folgt damit direkt aus Satz 1.6.3.1.





Next: Der Umordnungssatz für absolut
Up: Absolute und bedingte Konvergenz
Previous: Zum Zusammenhang zwischen absoluter
Contents
2003-09-05
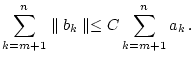
![]() und
und
![]() wegen Satz 1.2.3.1
die Konvergenz von
wegen Satz 1.2.3.1
die Konvergenz von
![]() .
Da
.
Da