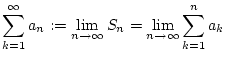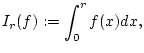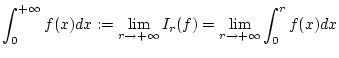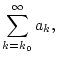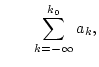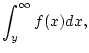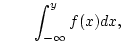Reihen über $\mathbb{N}\protect$ und uneigentlich Integrale auf $[0,+\infty [$.

Es sei $a_{.}:\mathbb{N}\to \mathbb{K}^{p}$, $\mathbb{K}=\{\mathbb{R},\mathbb{C}\}$, $p\in \mathbb{N}$, eine Folge von Gliedern $a_{k}\in \mathbb{K}^{p}$, $k\in \mathbb{N}$. Wir nennen

$$S_{n}:=\sum _{k=1}^{n}a_{k}$$ (1.1.1.1)

die $\textrm{n}$-te Partialsumme dieser Folge.

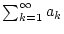
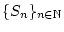
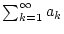
Definition 1.1.1.1   Eine Reihe $\sum _{k=1}^{\infty }a_{k}$ konvergiert genau dann, wenn die Folge $\{S_{n}\}_{n\in {\mathbb{N}}}$ der Partialsummen (1.1.1.1) konvergiert. Wir weisen dann dem Symbol $\sum _{k=1}^{\infty }a_{k}$ den entsprechenden Grenzwert

$$\sum _{k=1}^{\infty }a_{n}:=\lim _{n\to \infty }S_{n}=\lim _{n\to \infty }\sum _{k=1}^{n}a_{k}$$

zu.

Desweiteren sei $f:[0,+\infty [\, \to \mathbb{K}^{p}$ eine auf jedem Intervall $[0,r]$, $r\in \mathbb{R}$, $r>0$ integrierbare Funtion. Es sei

$$I_{r}(f):=\int _{0}^{r}f(x)dx,$$

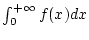
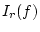
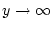
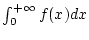
Definition 1.1.1.2   Das uneigentliche Integral $\int _{0}^{+\infty }f(x)dx$ konvergiert genau dann, wenn $I_{r}(f)$ einen Grenzwert für $y\to \infty$ besitzt. Wir weisen dann dem Symbol $\int _{0}^{+\infty }f(x)dx$ den Wert

$$\int _{0}^{+\infty }f(x)dx:=\lim _{r\to +\infty }I_{r}(f)=\lim _{r\to +\infty }\int _{0}^{r}f(x)dx$$

zu.

Diese Definitionen lassen sich leicht auf folgende Symbole übertragen

$$\sum _{k=k_{0}}^{\infty }a_{k}, \qquad \sum _{k=-\infty }^{k_{0}}a_{k}, \qquad k_{0}\in \mathbb{Z},$$

$$\int _{y}^{\infty }f(x)dx, \qquad \int _{-\infty }^{y}f(x)dx, \qquad y\in \mathbb{R}.$$