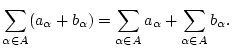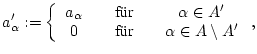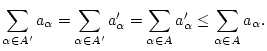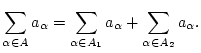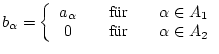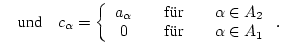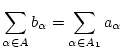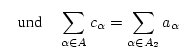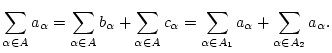Aus
![]() für alle
für alle
![]() folgt
folgt
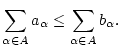
Konvergieren beide Reihen
![]() und
und
![]() , so konvergiert auch die Reihe
, so konvergiert auch die Reihe
![]() und
und
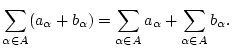
Folgende Aussage ist eine direkte Verallgemeinerung von Satz 1.2.3.1 (Additivität) und Satz 1.3.1.1 (Monotonität).
Aus
![]() für alle
für alle
![]() folgt
folgt
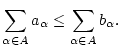
Konvergieren beide Reihen
![]() und
und
![]() , so konvergiert auch die Reihe
, so konvergiert auch die Reihe
![]() und
und