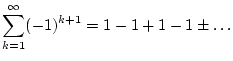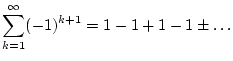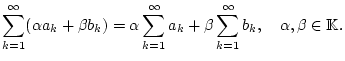Verallgemeinerte Summationsmethoden.

In den Anwendungen trifft man häufig auf Reihen, welche im üblichen Sinne divergieren. Um mit diesem Objekten mathematisch arbeiten zu können, wendet man verallgemeinerte Summationsmethoden an. Dabei handelt es sich um Regeln, wie man einem symbolischen Ausdruck, z.B.

$$\sum _{k=1}^{\infty }(-1)^{k+1}=1-1+1-1\pm \ldots$$

einen Zahlenwert zuordnet.^1.5Um von einer verallgemeinerten Summation zu sprechen, sollen diese Methoden folgende zwei Prinzipien erfüllen:

• Die Linearität: Konvergieren die Reihen $\sum _{k=1}^{\infty }a_{k}$ und $\sum _{k=1}^{\infty }b_{k}$ mit Summanden $a_{k},b_{k}\in \mathbb{K}^{p}$ nach einer verallgemeinerten Summationsmethode, so konvergiert auch die Reihe $\sum _{k=1}^{\infty }(\alpha a_{k}+\beta b_{k})$ nach dieser Methode und es gilt
  $$\sum _{k=1}^{\infty }(\alpha a_{k}+... ...fty }a_{k}+\beta \sum _{k=1}^{\infty }b_{k},\quad \alpha ,\beta \in \mathbb{K}.$$

• Die Regularität: Konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ bedingt (im üblichen Sinne) gegen einen Wert $A$, so soll dieselbe Reihe $\sum _{k=1}^{\infty }a_{k}$ auch im Sinne der verallgemeinerten Summationsmethode gegen $A$ konvergieren.

Die unterschiedlichen Summationsmethoden lassen sich auf verschiedene Klassen von Reihen anwenden und verfügen dann aber auch über unterschiedliche analytische Eigenschaften. Wir diskutieren hier kurz zwei der verbreitesten Methoden und formulieren die Resultate ohne Beweis. Der interessierte Leser sei auf G.M. Fichtenholz: Differential- und Integralrechnung Band II S. 364-386 hingewiesen.