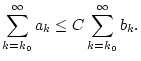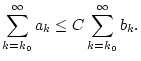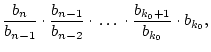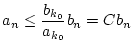Das Vergleichskriterium.

Alle folgende Konvergenzkriterien basieren im wesentlichen auf Satz 1.3.1.1 und Aufgabe 1.3.1.2, welchen wir hier nochmals in leicht modifizierter Form anführen. Wir überlassen dem Leser die Adaption der Beweise.

Satz 1.4.1.1   Es gelte $0\leq a_{k}\leq Cb_{k}$, für $k\geq k_{0}$, $k\in \mathbb{N}$ und geeignetes $C>0$. Divergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$, so divergiert auch die Reihe $\sum _{k=1}^{\infty }b_{k}$. Konvergiert andererseits die Reihe $\sum _{k=1}^{\infty }b_{k}$, so konvergiert auch die Reihe $\sum _{k=1}^{\infty }a_{k}$ und es gilt

$$\sum _{k=k_{0}}^{\infty }a_{k}\leq C\sum _{k=k_{0}}^{\infty }b_{k}.$$

 

Satz 1.4.1.2   Es seien $f,g:[0,+\infty [\to [0,+\infty [$ Funktionen, welche auf jedem endlichen Intervall $[0,c]$ integrierbar sind. Es gelte $f(x)\leq Cg(x)$ für $x\geq x_{0}$, und geeignetes $C>0$. Divergiert das Integral $\int _{0}^{\infty }f(x)dx$, so divergiert auch $\int _{0}^{\infty }g(x)dx$. Konvergiert andererseits das uneigentliche Integral $\int _{0}^{\infty }g(x)dx$, so konvergiert auch $\int _{0}^{\infty }f(x)dx$ und es gilt

$$\int _{x_{0}}^{\infty }f(x)dx\leq C\int _{x_{0}}^{\infty }g(x)dx\, .$$ (1.4.1.1)

Für Reihen erweist sich oft folgende Variante dieses Kriteriums als nützlich.

Satz 1.4.1.3   Es gelte $a_{k}>0$ und $b_{k}>0$ für $k\geq k_{0}$ sowie

$$\frac{a_{k+1}}{a_{k}}\leq \frac{b_{k+1}}{b_{k}} \quad \mbox {für\, alle}\quad k\geq k_{0}.$$ (1.4.1.2)

Konvergiert die Reihe $\sum _{k=1}^{\infty }b_{k}$, so konvergiert auch $\sum _{k=1}^{\infty }a_{k}$. Divergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$, so divergiert auch die Reihe $\sum _{k-1}^{\infty }b_{k}$.

$\blacktriangleright$ Wegen

$$a_{n} = \frac{a_{n}}{a_{n-1}}\cdot \frac{a_{n-1}}{a_{n-2}}\cdot \, \ldots \, \cdot \frac{a_{k_{0}+1}}{a_{k_{0}}}\cdot a_{k_{0}},$$

$$b_{n} = \frac{b_{n}}{b_{n-1}}\cdot \frac{b_{n-1}}{b_{n-2}}\cdot \, \ldots \, \cdot \frac{b_{k_{0}+1}}{b_{k_{0}}}\cdot b_{k_{0}},$$

folgt aufgrund von (1.4.1.2) die Ungleichung

$$a_{n}\leq \frac{b_{k_{0}}}{a_{k_{0}}}b_{n}=Cb_{n}$$$$\quad \mbox {für\, alle}\quad n\geq k_{0}.$$

Es verbleibt die Anwendung von Satz 1.4.1.1. $\blacktriangleleft$