



Next: Das Quotientenkriterium in Limesform.
Up: Konvergenzkriterien für Reihen mit
Previous: Das Vergleichskriterium in Limesform.
Contents
Satz 1.5.3.1
Es sei
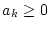 für
für
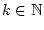 .
Gilt
.
Gilt
![$ \limsup_{k\to\infty}\sqrt[k]{a_k}<1$](img553.png) , dann konvergiert die
Reihe
, dann konvergiert die
Reihe
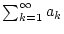 . Falls hingegen
. Falls hingegen
![$ \limsup_{k\to\infty}\sqrt[k]{a_k}>1$](img554.png) ,
dann divergiert die Reihe
,
dann divergiert die Reihe
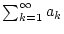 .
.
 Aus
Aus
![$ s=\limsup_{k\to\infty}\sqrt[k]{a_k}<1$](img555.png) folgt
folgt
![$ \sqrt[k]{a_k}<r$](img556.png) für
für
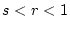 und
und
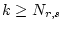 . Falls hingegen
. Falls hingegen
![$ \limsup_{k\to\infty}\sqrt[k]{a_k}>1$](img554.png) , dann
existieren unendlich viele
, dann
existieren unendlich viele 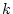 mit
mit 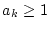 . Damit folgen
die Aussagen direkt aus Satz 1.4.2.1.
. Damit folgen
die Aussagen direkt aus Satz 1.4.2.1.

2003-09-05