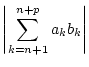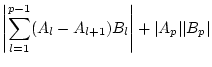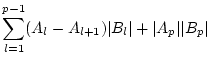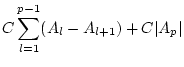Next: Das Leibniz-Kriterium für alternierende
Up: Konvergenzkriterien für im Allgemeinen
Previous: Das Abelsche Kriterium.
Contents
Satz 1.7.3.1
Die Folge reeller Zahlen
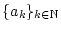 sei monoton
und es gelte
sei monoton
und es gelte
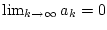 . Desweiteren sei für
. Desweiteren sei für
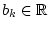 ,
,
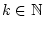 die Folge der
Partialsummen
die Folge der
Partialsummen
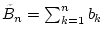 ,
,
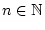 ,
beschränkt. Dann ist die Reihe
,
beschränkt. Dann ist die Reihe
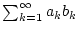 konvergent.
konvergent.
 Wir betrachten den Fall einer monoton fallenden gegen Null konvergenten
Folge
Wir betrachten den Fall einer monoton fallenden gegen Null konvergenten
Folge
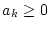 . Es sei
. Es sei
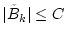 für
für
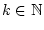 . Mit der Notation des Beweises von Satz 1.7.2.1
(und damit
. Mit der Notation des Beweises von Satz 1.7.2.1
(und damit
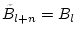 sowie
sowie
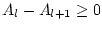 )
gilt
)
gilt
Da
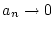 für
für
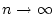 , so folgt
, so folgt
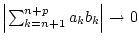 für
für
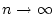 . Nach dem Cauchy-Kriterium konvergiert damit
die Reihe
. Nach dem Cauchy-Kriterium konvergiert damit
die Reihe
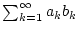 .
.

2003-09-05