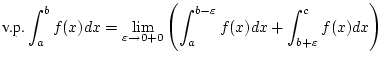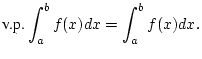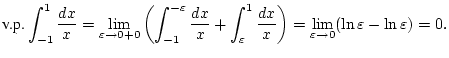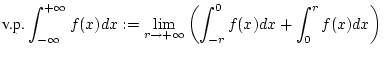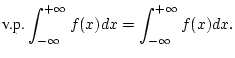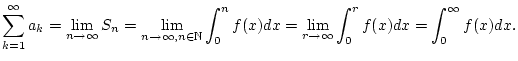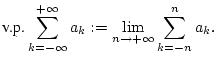Next: Wichtige Eigenschaften von Reihen
Up: Grundlegende Definitionen
Previous: Uneigentliche Integrale auf endlichem
Contents
Das uneigentliche Integral im letzten Beispiel divergiert, da die
Grenzwerte für
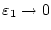 und
und
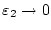 separat nicht existieren Würde man hingegen
separat nicht existieren Würde man hingegen
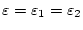 setzten und beide Grenzwerte in (1.1.4.2) zu
setzten und beide Grenzwerte in (1.1.4.2) zu
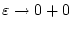 zusammenfassen, so konvergiert dieser Ausdruck gegen
zusammenfassen, so konvergiert dieser Ausdruck gegen 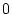 , die
beiden unendlichen Anteile löschen einander aus, wenn man sich von
beisen Seiten mit gleicher Geschwindigkeit der Singularität nähert.
Dies motiviert folgende Definition des Hauptwertes nach Cauchy:
, die
beiden unendlichen Anteile löschen einander aus, wenn man sich von
beisen Seiten mit gleicher Geschwindigkeit der Singularität nähert.
Dies motiviert folgende Definition des Hauptwertes nach Cauchy:
Definition 1.1.5.1
Die Funktion
![% latex2html id marker 21183
$ f:[a,c[\cup ]c,b]\to \mathbb{K}^{p} $](img114.png)
sei für beliebiges
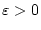
integrierbar auf
![$ [a,c-\varepsilon ] $](img115.png)
und
![$ [c+\varepsilon ,b] $](img116.png)
. Wir sagen, daß das uneigentliche Integral
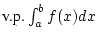
im Sinne des
Cauchyschen
Hauptwertes konvergiert, wenn der Grenzwert
existiert.
Aufgabe 1.1.5.2
Existiert das uneigentliche Integral
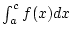
, so
existiert auch der Cauchysche Hauptwert
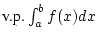
und
Beispiel 1.1.5.3
Es gilt
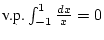
, da
Wir betrachten nun Funktionen
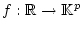 ,
welche auf jedem beschränkten Intervall integrierbar sind.
,
welche auf jedem beschränkten Intervall integrierbar sind.
Definition 1.1.5.4
Das uneigentliche Integral
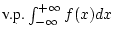
konvergiert im Sinne des Hauptwertes nach Cauchy, wenn der Grenzwert
existiert.
Aufgabe 1.1.5.5
Konvergiert das uneigentliche Integral
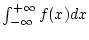
,
so existiert auch
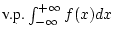
und
Finden Sie umgekehrt Beispiele für Funktionen, für welche
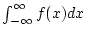
divergiert, aber
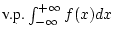
existiert.
Jede Reihe
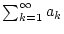 kann man auch als uneigentliches
Integral
kann man auch als uneigentliches
Integral
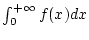 mit dem Integranden
verstehen. Offensichtlich konvergieren
mit dem Integranden
verstehen. Offensichtlich konvergieren
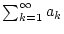 und
und
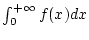 gleichzeitig und nehmen dann
ein und denselben Wert an, denn
Diese Idee läßt sich direkt auf Reihen
gleichzeitig und nehmen dann
ein und denselben Wert an, denn
Diese Idee läßt sich direkt auf Reihen
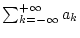 übertragen. Konvergiert das dabei entstehende Integral
übertragen. Konvergiert das dabei entstehende Integral
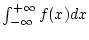 nur im Sinne des Cauchyschen Hauptwerkes, so erhält man auch die Definition
des Hauptwertes einer Reihe über
nur im Sinne des Cauchyschen Hauptwerkes, so erhält man auch die Definition
des Hauptwertes einer Reihe über
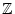
Alle hier angeführten Definitionen lassen sich sofort auf Folgen mit
Werten in allgemeinen normierten Räumen verallgemeinern.




Next: Wichtige Eigenschaften von Reihen
Up: Grundlegende Definitionen
Previous: Uneigentliche Integrale auf endlichem
Contents
2003-09-05
![]() und
und
![]() separat nicht existieren Würde man hingegen
separat nicht existieren Würde man hingegen
![]() setzten und beide Grenzwerte in (1.1.4.2) zu
setzten und beide Grenzwerte in (1.1.4.2) zu
![]() zusammenfassen, so konvergiert dieser Ausdruck gegen
zusammenfassen, so konvergiert dieser Ausdruck gegen ![]() , die
beiden unendlichen Anteile löschen einander aus, wenn man sich von
beisen Seiten mit gleicher Geschwindigkeit der Singularität nähert.
Dies motiviert folgende Definition des Hauptwertes nach Cauchy:
, die
beiden unendlichen Anteile löschen einander aus, wenn man sich von
beisen Seiten mit gleicher Geschwindigkeit der Singularität nähert.
Dies motiviert folgende Definition des Hauptwertes nach Cauchy: