- ...1.1
- Das kartesische Produkt
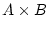 läßt sich in dieser Notation
als
läßt sich in dieser Notation
als
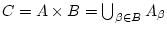 mit
mit
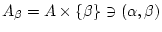 realisieren.
realisieren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1.2
- Diese Argumentation gilt auch, wenn eine oder beide der Folgen
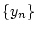 bzw.
bzw. 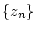 bestimmt divergiert.
bestimmt divergiert.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1.3
- Hier bezeichnet
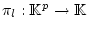 die
Projektion von
die
Projektion von
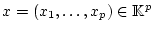 auf
die
auf
die 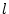 -te Komponente
-te Komponente
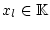 in kartesischen
Koordination.
in kartesischen
Koordination.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Kriterien1.4
- z.B. Wurzelkriterium, Quotientenkriterium, Kriteria von Raabe bzw.
Kummer
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1.5
- Auch bei der üblichen Definition der Reihe wird dem Symbol
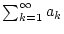 nach einer vorgegebenen Regel ein Wert zugeordnet. Auch wenn diese
Definition anschaulich gut motiviert ist, so ist es doch nur nur eine
spezielle Möglichkeit, den Begriff der endlichen Summe zu verallgemeinern.
nach einer vorgegebenen Regel ein Wert zugeordnet. Auch wenn diese
Definition anschaulich gut motiviert ist, so ist es doch nur nur eine
spezielle Möglichkeit, den Begriff der endlichen Summe zu verallgemeinern.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
stetig2.1
- Hierbei spielt
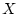 die Rolle der Parametermenge
die Rolle der Parametermenge 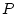 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
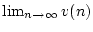 .2.2
.2.2
- Setzt man o.B.d.A. die gleichmäßige Konvergenz von (2.2.2.1)
voraus, so konvergiert im Rahmen von Satz 2.2.2.1 (2.2.2.2)
nicht notwendigerweise gleichmäßig. Damit kann man die Argumentation
von Schritt 1 des Beweises nicht einfach duplizieren.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2.3
- Da
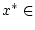
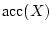 , so existiert mindestens eine solche
Folge.
, so existiert mindestens eine solche
Folge.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gleichmäßig2.4
- Gleichmäßigkeit von (2.4.0.1) bezüglich
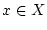 oder von (2.4.0.2) bezüglich
oder von (2.4.0.2) bezüglich 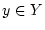
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... eingesetzt2.5
- Wo wurden für reelle Ableitung spezifische Aussagen benützt?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
konvergiert2.6
- Beweisen Sie dies!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... berechnen2.7
- Geben sie die Formel für
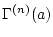 an!
an!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sei3.1
- Hier bezeichnet
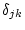 das Kronecker-Symbol.
das Kronecker-Symbol.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...3.2
- Hier fließt ein, daß
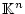 ein endlichdimensionaler
Raum ist, siehe auch die weiteren Kommentare in diesem Abschnitt.
ein endlichdimensionaler
Raum ist, siehe auch die weiteren Kommentare in diesem Abschnitt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3.3
- Man setze in der Definition der Linearität
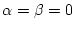 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... und3.4
-
![% latex2html id marker 29314
$ C^{1}([a,b],\mathbb {R}) $](img2007.png) ist die Menge aller stetigen Funktionen,
welche in
ist die Menge aller stetigen Funktionen,
welche in ![$ ]a,b[ $](img1145.png) differenzierbar sind und deren Ableitung sich
zu stetigen Funktionen auf
differenzierbar sind und deren Ableitung sich
zu stetigen Funktionen auf ![$ [a,b] $](img87.png) fortsetzen lassen.
fortsetzen lassen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wenn3.5
- Wir erinnern hier an die Definition des Landau-Symboles. Für eine
Funktion
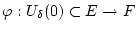 ,
,
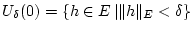 ,
schreibt man
,
schreibt man
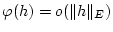 für
für 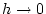 genau dann, wenn die Aussage
wahr ist.
genau dann, wenn die Aussage
wahr ist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...3.6
- Vervollständigen Sie diese Abschätzung!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... erhält3.7
- Vollziehen Sie diese Rechnung in der Schreibweise (3.3.3.1)
nach!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... damit3.8
- Verifizieren Sie diesen Schritt im Detail.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.