



Next: Der Raum der stetigen
Up: Der Raum der stetigen
Previous: Beschränkte lineare Operatoren.
Contents
(I) Es sei 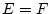 . Die Identität
. Die Identität
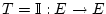 gegeben durch
gegeben durch
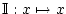 ,
, 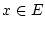 ist ein
stetiger linearer Operator.
ist ein
stetiger linearer Operator.
(II) Für gegebene
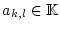 mit
mit
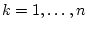 und
und
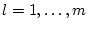 induziert die Matrix
induziert die Matrix
die lineare Abbildung
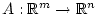 gegeben durch
gegeben durch
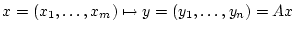 nach der Formel
nach der Formel
Aufgabe 3.2.4.1
Beweisen Sie die Stetigkeit in diesen beiden Beispielen!
(III) Es sei
![% latex2html id marker 29295
$ D_{T}=E=F=C([a,b],\mathbb{R}) $](img1999.png) . Für eine
gegebene Funktion
. Für eine
gegebene Funktion
![% latex2html id marker 29297
$ \varphi \in C([a,b],\mathbb{R}) $](img2000.png) betrachten
wir die Abbildung
für
betrachten
wir die Abbildung
für
![$ x\in [a,b] $](img1194.png) . Dies ist offensichtlich eine lineare Abbildung.
Die Abschätzung
mit
. Dies ist offensichtlich eine lineare Abbildung.
Die Abschätzung
mit
![$ C_{\varphi }=\max _{x\in [a,b]}\vert\varphi (x)\vert $](img2004.png) zeigt, daß
zeigt, daß
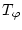 beschränkt und damit stetig ist.
beschränkt und damit stetig ist.
(IV) Es sei
![% latex2html id marker 29310
$ E=F=C([0,1],\mathbb{R}) $](img2006.png) und3.4
und3.4
![% latex2html id marker 29320
$ D_{d}=C^{1}([0,1],\mathbb{R}) $](img2008.png) . Wir betrachten die Abbildung
. Wir betrachten die Abbildung
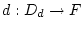 gegeben durch
gegeben durch
Aufgabe 3.2.4.2
Zeigen Sie, daß
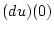
die rechtsseitige Ableitung von
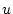
im Punkt
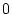
und
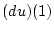
die linksseitige Ableitung von
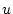
im Punkt
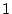
ist.
Der Operator 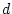 ist offensichtlich eine lineare Abbildung. Auf
der anderen Seite ist der so definierte Operator ist nicht stetig
von
ist offensichtlich eine lineare Abbildung. Auf
der anderen Seite ist der so definierte Operator ist nicht stetig
von
![% latex2html id marker 29362
$ D_{d}\subset C([0,1],\mathbb{R}) $](img2017.png) nach
nach
![% latex2html id marker 29364
$ C([0,1],\mathbb{R}) $](img2018.png) .
Dazu betrachten wir die Funktionenfolge
Dann gilt
.
Dazu betrachten wir die Funktionenfolge
Dann gilt
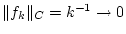 und damit
und damit
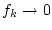 in für
in für
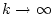 , während
Da
, während
Da
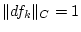 , so konvergiert
, so konvergiert 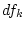 nicht
gegen
nicht
gegen 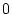 in
in
![% latex2html id marker 29382
$ C([0,1],\mathbb{R}) $](img2025.png) , also ist der Operator
, also ist der Operator
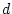 nicht stetig von
nicht stetig von
![% latex2html id marker 29386
$ D_{d}\subset C([0,1],\mathbb{R}) $](img2026.png) nach
nach
![% latex2html id marker 29388
$ C([0,1],\mathbb{R}) $](img2027.png) .
.
(V) Wir betrachten auf der Funktionenmenge
![% latex2html id marker 29390
$ C^{1}([a,b],\mathbb{R}) $](img2028.png) das Funktional
das Funktional
mit
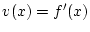 für
für
![$ x\in ]a,b[ $](img1173.png) sowie
sowie
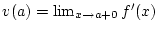 und
und
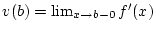 .
.
Aufgabe 3.2.4.3
Zeigen Sie, daß
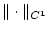
eine Norm auf
![% latex2html id marker 29410
$ C^{1}([a,b],\mathbb{R}) $](img2034.png)
definiert.
Es sei nun
![% latex2html id marker 29413
$ D_{d}=E=C^{1}([0,1],\mathbb{R}) $](img2035.png) und
und
![% latex2html id marker 29415
$ F=C([0,1],\mathbb{R}) $](img2036.png) .
Wir betrachten die lineare Abbildung
.
Wir betrachten die lineare Abbildung 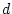 gegeben in (3.2.4.1)-(3.2.4.2)
als Operator von
gegeben in (3.2.4.1)-(3.2.4.2)
als Operator von
![% latex2html id marker 29419
$ D_{d}=E=C^{1}([0,1],\mathbb{R}) $](img2037.png) nach
nach
![% latex2html id marker 29421
$ F=C([0,1],\mathbb{R}) $](img2038.png) .
Die Abschätzung
zeigt, daß
.
Die Abschätzung
zeigt, daß 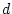 zwischen diesen beiden Räumen ein beschränkter
und damit stetiger Operator ist.
zwischen diesen beiden Räumen ein beschränkter
und damit stetiger Operator ist.
Das letzte Beispiel illustriert nochmals, daß die Stetigkeit einer
Abbildung von der Wahl der Metrik auf dem Definitions- wie auf dem
Wertebereich abhängt.
Aufgabe 3.2.4.4
Zeigen Sie, daß
![% latex2html id marker 29433
$ C^{1}([0,1],\mathbb{R}) $](img2040.png)
mit der Norm
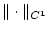
ein Banachraum ist. Verwenden Sie dazu die Vollständigkeit von
![% latex2html id marker 29437
$ C([0,1],\mathbb{R}) $](img2041.png)
sowie Satz
2.6.1.1.
(VI) Es sei 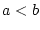 ,
,
![% latex2html id marker 29443
$ D_{J}=E=C([a,b],\mathbb{K}) $](img2042.png) und
und
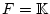 . Wir betrachten die Abbildung
Dies ist ein linearer Operator und wegen
ist
. Wir betrachten die Abbildung
Dies ist ein linearer Operator und wegen
ist 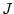 ein beschränkter und damit stetiger Operator von
ein beschränkter und damit stetiger Operator von
![% latex2html id marker 29454
$ C([a,b],\mathbb{K}) $](img2047.png) nach
nach
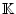 .
.




Next: Der Raum der stetigen
Up: Der Raum der stetigen
Previous: Beschränkte lineare Operatoren.
Contents
2003-09-05
![]() . Die Identität
. Die Identität
![]() gegeben durch
gegeben durch
![]() ,
, ![]() ist ein
stetiger linearer Operator.
ist ein
stetiger linearer Operator.
![]() mit
mit
![]() und
und
![]() induziert die Matrix
induziert die Matrix

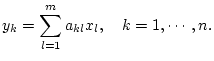
![]() und3.4
und3.4
![]() . Wir betrachten die Abbildung
. Wir betrachten die Abbildung
![]() gegeben durch
gegeben durch
![]() das Funktional
das Funktional
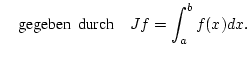
![$\displaystyle \vert Jf\vert=\left\vert \int _{a}^{b}f(x)dx\right\vert \leq \int...
... f(x)\vert dx\leq (b-a)\max _{x\in [a,b]}\vert f(x)\vert=(b-a)\Vert f\Vert _{C}$](img2046.png)