



Next: Der Beweis von Satz
Up: Der Hauptsatz der Differentialrechnung
Previous: Der Hauptsatz der Differentialrechnung.
Contents

 Wir wählen
Dann gilt
Wir wählen
Dann gilt
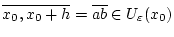 für
für
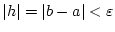 . Nach Satz 3.5.2.1
folgt aus (3.5.2.1) die Ungleichung
Die Stetigkeit von
. Nach Satz 3.5.2.1
folgt aus (3.5.2.1) die Ungleichung
Die Stetigkeit von
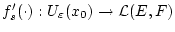 im Punkt
im Punkt 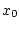 impliziert
und damit3.8
Daraus folgt
Also ist die Funktion
impliziert
und damit3.8
Daraus folgt
Also ist die Funktion 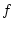 im Punkt
im Punkt 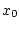 Frechet-differenzierbar
und es gilt
Frechet-differenzierbar
und es gilt
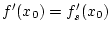 .
.

2003-09-05