



Next: Beispiele.
Up: Die Frechet-Ableitung
Previous: Die Definition der Frechet-Ableitung.
Contents
Satz 3.3.2.1
Ist die Funktion 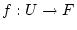 im Punkt
im Punkt
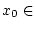
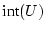 Frechet-differenzierbar, so ist
Frechet-differenzierbar, so ist
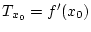 eindeutig
bestimmt.
eindeutig
bestimmt.
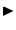 Angenommen, es gibt zwei Operatoren
Angenommen, es gibt zwei Operatoren
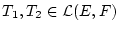 mit
mit
Dann folgt
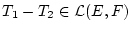 und
daß heißt
und
daß heißt
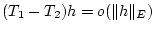 für
für
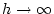 .
Damit existiert für jedes
.
Damit existiert für jedes
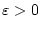 ein
ein
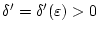 ,
so daß
Aufgrund der Homogenität der Norm und der Linearität von
,
so daß
Aufgrund der Homogenität der Norm und der Linearität von
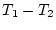 gilt diese Abschätzung auch für beliebige
gilt diese Abschätzung auch für beliebige 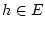 , woraus
für beliebiges
, woraus
für beliebiges
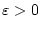 folgt. Damit ist
folgt. Damit ist
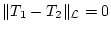 .
Aus den Axiomen der Norm von
.
Aus den Axiomen der Norm von
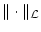 folgt
folgt
Aufgabe 3.3.2.2
Ist die Funktion
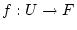
im Punkt
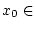
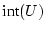
Frechet-differenzierbar, so ist
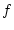
in diesem Punkt stetig.
Aufgabe 3.3.2.3
Es seien
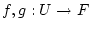
zwei Funktionen, die im Punkt
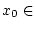
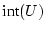
Frechet-differenzierbar sind. Zeigen Sie, daß dann die Abbildung
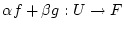
für beliebige
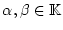
im Punkt
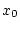
Frechet-differenzierbar ist und dabei
gilt.
 Zunächst analysieren wir die Struktur des Ausdruckes (3.3.2.1).
Da
Zunächst analysieren wir die Struktur des Ausdruckes (3.3.2.1).
Da
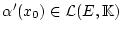 ,
so ist für jedes
,
so ist für jedes 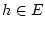 der Ausdruck
der Ausdruck
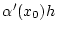 ein Element in
ein Element in
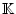 . Also ist wegen
. Also ist wegen
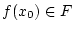 der Ausdruck
der Ausdruck
als Produkt von
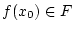 mit dem Skalar
mit dem Skalar
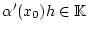 zu verstehen, dies ist ein Element in
zu verstehen, dies ist ein Element in 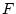 . Desweiteren gilt
. Desweiteren gilt
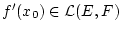 und damit
und damit
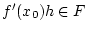 . Da
. Da
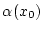 Werte in
Werte in
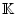 annimmt, so ist
das Produkt des Skalars
annimmt, so ist
das Produkt des Skalars
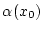 mit
mit
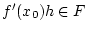 ,
d.h. selbst ein Element in
,
d.h. selbst ein Element in 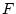 . Die Summe beider Ausdrücke
. Die Summe beider Ausdrücke
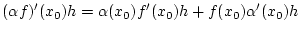 |
(3.3.2.2) |
ist demnach ein Element in 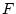 . Es ist leicht zu sehen, daß
(3.3.2.2) dabei für festes
. Es ist leicht zu sehen, daß
(3.3.2.2) dabei für festes 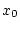 eine lineare
Abbildungen von
eine lineare
Abbildungen von 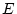 nach
nach 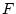 in der Variablen
in der Variablen 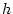 definiert.
Da
definiert.
Da
mit
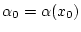 ,
,
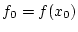 sowie
so gilt zudem
sowie
so gilt zudem
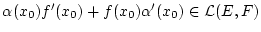 .
.
Schreibt man nun
so folgt
Man verifiziert leicht, daß3.6
für 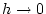 , was den Beweis abschließt.
, was den Beweis abschließt.
 Wegen
Wegen
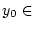
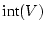 existiert ein
existiert ein 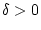 mit
mit
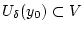 . Nach Aufgabe 3.3.2.2
ist
. Nach Aufgabe 3.3.2.2
ist 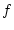 im Punkt
im Punkt 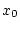 stetig, d.h. es existiert ein
stetig, d.h. es existiert ein
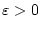 mit
mit
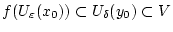 .
Damit ist
.
Damit ist 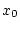 ein innerer Punkt des Definitionsbereiches
ein innerer Punkt des Definitionsbereiches
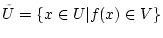 von
von 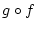 .
.
Da
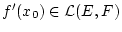 und
und
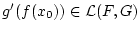 ,
so ist nach Aufgabe 3.2.6.1
,
so ist nach Aufgabe 3.2.6.1
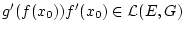 .
Aus
.
Aus
folgt
mit
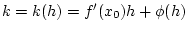 . Es folgt wegen der
Linearität von
. Es folgt wegen der
Linearität von
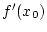 und der Abschätzung
und der Abschätzung
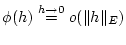 auch
für genügend kleine
auch
für genügend kleine
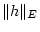 und damit
für
und damit
für
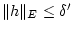 . Dann ist
. Dann ist
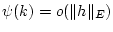 für
für 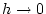 und damit
Da weiterhin aufgrund der Linearität von
und damit
Da weiterhin aufgrund der Linearität von
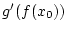 die Abschätzung
gilt, so folgt (3.3.2.3).
die Abschätzung
gilt, so folgt (3.3.2.3).




Next: Beispiele.
Up: Die Frechet-Ableitung
Previous: Die Definition der Frechet-Ableitung.
Contents
2003-09-05
![]() Angenommen, es gibt zwei Operatoren
Angenommen, es gibt zwei Operatoren
![]() mit
mit
![]() Zunächst analysieren wir die Struktur des Ausdruckes (3.3.2.1).
Da
Zunächst analysieren wir die Struktur des Ausdruckes (3.3.2.1).
Da
![]() ,
so ist für jedes
,
so ist für jedes ![]() der Ausdruck
der Ausdruck
![]() ein Element in
ein Element in
![]() . Also ist wegen
. Also ist wegen
![]() der Ausdruck
der Ausdruck
![]() Wegen
Wegen
![]()
![]() existiert ein
existiert ein ![]() mit
mit
![]() . Nach Aufgabe 3.3.2.2
ist
. Nach Aufgabe 3.3.2.2
ist ![]() im Punkt
im Punkt ![]() stetig, d.h. es existiert ein
stetig, d.h. es existiert ein
![]() mit
mit
![]() .
Damit ist
.
Damit ist ![]() ein innerer Punkt des Definitionsbereiches
ein innerer Punkt des Definitionsbereiches
![]() von
von ![]() .
.
![]() und
und
![]() ,
so ist nach Aufgabe 3.2.6.1
,
so ist nach Aufgabe 3.2.6.1
![]() .
Aus
.
Aus