



Next: Kompaktheit in endlich- und
Up: Endlich- und Unendlichdimensionale Vektorräume
Previous: Zur Dimension normierter Vektorräume.
Contents
Es gibt signifikante Unterschiede zwischen endlich- und unendlichdimensionalen
normierten Räumen, wie wir hier an zwei Beispielen illustrieren wollen.
Diese dienen vor allem zur Warnung davor, ``gewohnte'' Eigenschaften
der Räume
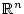 und
und
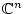 ohne weiteres
auf den unedlichdimensionalen Fall zu verallgemeinern.
ohne weiteres
auf den unedlichdimensionalen Fall zu verallgemeinern.
Auf den Räumen
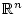 und
und
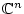 kann
man verschiedene Normen definieren. Für einen Vektor
kann
man verschiedene Normen definieren. Für einen Vektor
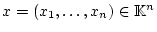 kann man neben der Euklidschen Norm
kann man neben der Euklidschen Norm
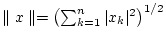 z.B. die Normen
z.B. die Normen
definieren.
Aufgabe 3.1.3.1
Beweisen Sie, daß
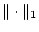
und
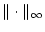
Normen auf
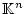
sind.
 Zunächst stellen wir fest, daß
Zunächst stellen wir fest, daß
Es sei3.1
 ,
,
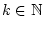 und damit gilt für
und damit gilt für
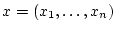 die Zerlegung
die Zerlegung
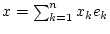 .
Dann folgt für die Norm
.
Dann folgt für die Norm
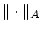 nach der Dreiecksungleichung
und der Homogenität die Abschätzung
nach der Dreiecksungleichung
und der Homogenität die Abschätzung
mit
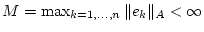 . Aus
der Dreiecksungleichung für
. Aus
der Dreiecksungleichung für
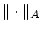 folgt
und damit ist wegen
die Abbildung
folgt
und damit ist wegen
die Abbildung
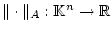 stetig bezüglich der Euklidschen Norm
stetig bezüglich der Euklidschen Norm
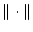 .
.
Wir betrachten nun die Restriktion dieser Funktion
Die Menge 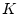 ist bezüglich
ist bezüglich
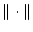 eine abgeschlossene und beschränkte Teilmenge von
eine abgeschlossene und beschränkte Teilmenge von
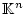 ;
nach dem Satz von Bolzano ist diese Menge kompakt.3.2 Die stetige Funktion
;
nach dem Satz von Bolzano ist diese Menge kompakt.3.2 Die stetige Funktion
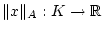 nimmt
nach dem Satz von Weierstrass damit ihr
nimmt
nach dem Satz von Weierstrass damit ihr
für geeignete
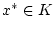 und
und
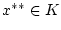 an. Da
an. Da
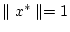 und damit
und damit
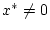 , so folgt
Desweiteren ist offensichtlich
, so folgt
Desweiteren ist offensichtlich
Für allgemeines
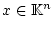 ,
, 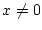 sei
sei
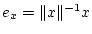 .
Damit gilt
.
Damit gilt
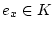 und
und
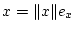 . Aus
. Aus
folgt nach Multiplikation mit
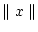 schließlich
Auf gleichem Wege folgt
Die Kombination der letzten beiden Ungleichungen beweist den Satz.
schließlich
Auf gleichem Wege folgt
Die Kombination der letzten beiden Ungleichungen beweist den Satz.
Der eben bewiesene Satz läßt sich leicht auf beliebige endlichdimensionale
normierte Räume verallgemeinern. Er gilt aber nicht für unendlichdimensionale
Räume, wie wir an folgendem Gegenbeispiel illustrieren.
Auf der Menge
![% latex2html id marker 28814
$ C([a,b],\mathbb{K}) $](img1889.png) ,
, 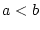 , führen wir
neben der kanonischen Norm
, führen wir
neben der kanonischen Norm
das Funktional
ein. Da für stetige Funktionen 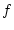 auch
auch 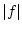 stetig und
damit integrierbar ist, so ist die Größe
stetig und
damit integrierbar ist, so ist die Größe
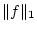 wohldefiniert.
wohldefiniert.
Lemma 3.1.3.3
Das Funktional
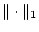 stellt eine Norm auf
der Funktionenmenge
stellt eine Norm auf
der Funktionenmenge
![% latex2html id marker 28836
$ C([a,b],\mathbb{K}) $](img1894.png) dar.
dar.
 Tatsächlich, für beliebiges
Tatsächlich, für beliebiges
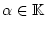 und
und
![% latex2html id marker 28842
$ f\in C([a,b],\mathbb{K}) $](img1896.png) folgt
folgt
Desweiteren folgt aus der Dreiecksungleichung für den Absolutbetrag
für beliebige
![% latex2html id marker 28866
$ f,g\in C([a,b],\mathbb{K}) $](img1903.png) . Wegen
. Wegen
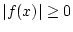 gilt offensichtlich
Ist
gilt offensichtlich
Ist 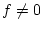 , d.h. gibt es ein
, d.h. gibt es ein
![$ x_{0}\in [a,b] $](img1907.png) mit
mit
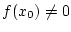 und folglich
und folglich
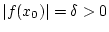 , so existiert aufgrund der
Stetigkeit von
, so existiert aufgrund der
Stetigkeit von 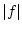 ein
ein
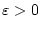 mit
und damit
mit
und damit
Wir betrachten nun die in (3.1.2.1)-(3.1.2.2)
definierten Funktionen 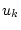 auf dem Intervall
auf dem Intervall
![$ [a,b]=[0,1] $](img1688.png) .
Man sieht leicht, daß
.
Man sieht leicht, daß
während
woraus bei
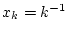 die Konvergenz
folgt. Damit können
die Konvergenz
folgt. Damit können
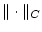 und
und
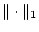 nicht äquivalent sein.
nicht äquivalent sein.
Wir betonen, daß die Funktionenmenge
![% latex2html id marker 28908
$ C([a,b],\mathbb{K}) $](img1919.png) bezüglich
der Norm
bezüglich
der Norm
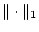 nicht vollständig ist.
Über die Struktur der ``Vervollständigung'' dieses Raumes bezüglich
der Integralnorm sprechen wir im Rahmen der Lebesgue-Theorie.
nicht vollständig ist.
Über die Struktur der ``Vervollständigung'' dieses Raumes bezüglich
der Integralnorm sprechen wir im Rahmen der Lebesgue-Theorie.




Next: Kompaktheit in endlich- und
Up: Endlich- und Unendlichdimensionale Vektorräume
Previous: Zur Dimension normierter Vektorräume.
Contents
2003-09-05
![]() und
und
![]() ohne weiteres
auf den unedlichdimensionalen Fall zu verallgemeinern.
ohne weiteres
auf den unedlichdimensionalen Fall zu verallgemeinern.
![]() und
und
![]() kann
man verschiedene Normen definieren. Für einen Vektor
kann
man verschiedene Normen definieren. Für einen Vektor
![]() kann man neben der Euklidschen Norm
kann man neben der Euklidschen Norm
![]() z.B. die Normen
z.B. die Normen
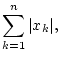
![]() Zunächst stellen wir fest, daß
Zunächst stellen wir fest, daß
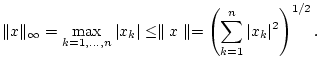
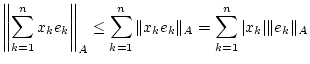
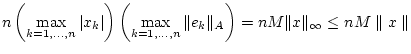
![]() ,
, ![]() sei
sei
![]() .
Damit gilt
.
Damit gilt
![]() und
und
![]() . Aus
. Aus
![]() ,
, ![]() , führen wir
neben der kanonischen Norm
, führen wir
neben der kanonischen Norm
![% latex2html id marker 28820
$\displaystyle \Vert f\Vert _{1}=\int _{a}^{b}\vert f(x)\vert dx\quad f\in C([a,b],\mathbb{K}),$](img1891.png)
![]() Tatsächlich, für beliebiges
Tatsächlich, für beliebiges
![]() und
und
![]() folgt
folgt
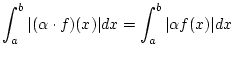
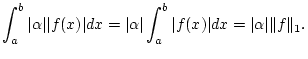
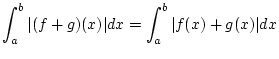
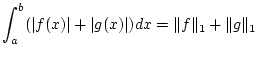
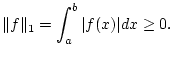
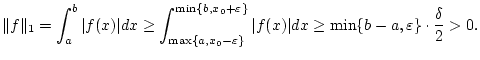
![]() auf dem Intervall
auf dem Intervall
![]() .
Man sieht leicht, daß
.
Man sieht leicht, daß
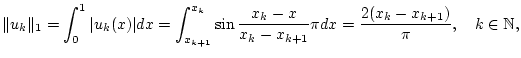
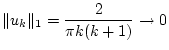
![]() bezüglich
der Norm
bezüglich
der Norm
![]() nicht vollständig ist.
Über die Struktur der ``Vervollständigung'' dieses Raumes bezüglich
der Integralnorm sprechen wir im Rahmen der Lebesgue-Theorie.
nicht vollständig ist.
Über die Struktur der ``Vervollständigung'' dieses Raumes bezüglich
der Integralnorm sprechen wir im Rahmen der Lebesgue-Theorie.