Schülerseminar Mathematik: Primzahlen

Priv.-Doz. Dr. Peter H. Lesky Hier können die Unterrichtseinheiten des Schülerseminars zum Thema Primzahlen online mitgemacht werden. Jede Einheit startet mit einem kurzen Einführungsvideo. Danach wechseln sich Arbeitsblätter mit Video-Sequenzen ab. Die Arbeitsblätter stehen zwischen den Videos an der Stelle, an der sie bearbeitet werden sollen. Es empfiehlt sich, die Arbeitsblätter zuerst auszudrucken.
Autor: P. Lesky (Photo).
Die Videos wurden gefilmt und geschnitten von Frau Elke Peter


1. Primzahlen

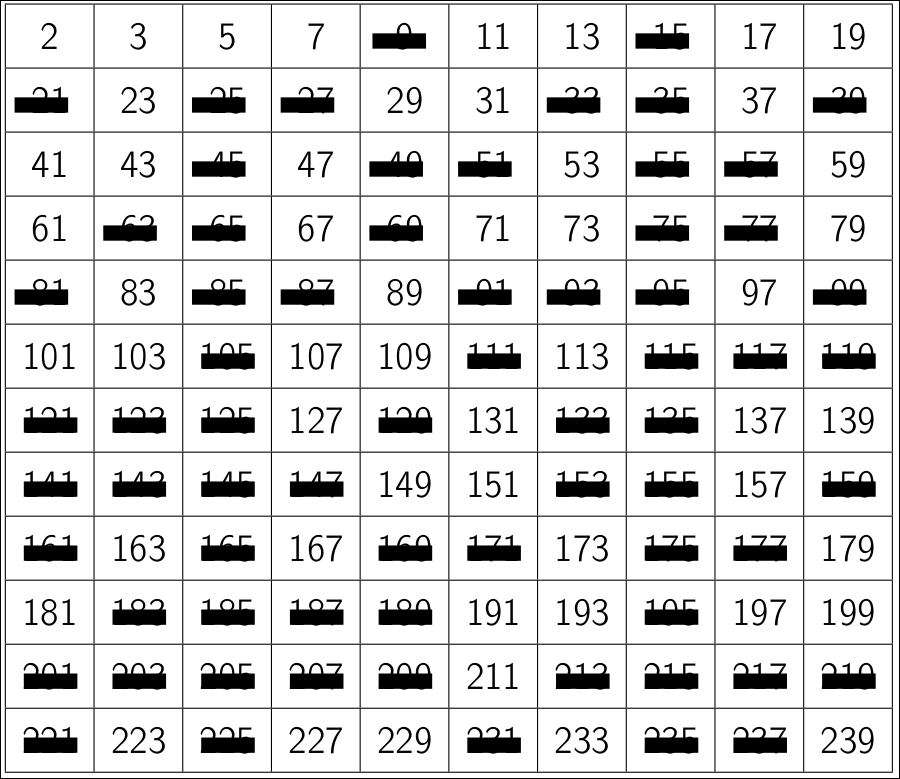
Sieb des Eratosthenes
  1. Video: Definitionen
  2. Arbeitsblatt 1: Sieb des Eratosthenes
  3. Video: Lösung von Arbeitsblatt 1, Primfaktorzerlegung
  4. Arbeitsblatt 2: Primfaktorzerlegung, Primzahlzwillinge und -drillinge
  5. Video: Lösung von Arbeitsblatt 2. Es gibt unendlich viele Primzahlen
  6. Arbeitsblatt 3: Primfakultät
  7. Video: Besprechung der Aufgaben auf Blatt 3
  8. Arbeitsblatt 4: Schriftliche Aufgaben
Du kannst Deine Lösungen der schriftlichen Aufgaben
an zirkel@mathematik.uni-stuttgart.de schicken.
Dann erhältst Du eine Musterlösung.

2. Kongruenzen

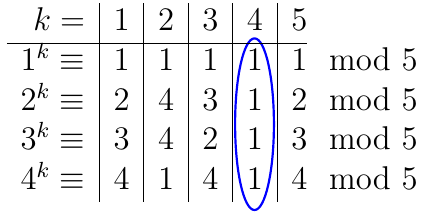
Kleiner Satz von Fermat
  1. Video: Begrüßung
  2. Arbeitsblatt 1: Teilen durch 9 mit Rest
  3. Video: Lösung von Aufgabe 1, Kongruenz von Zahlen
  4. Arbeitsblatt 2: Kongruenz-Gleichungen
  5. Video: Lösung von Aufgabe 2, Rechenregeln für Kongruenzen
  6. Arbeitsblatt 3: Rechnen mit Kongruenzen
  7. Video: Besprechung der Aufgaben auf Blatt 3, Kleiner Satz von Fermat
  8. Arbeitsblatt 4: Teilen durch 11
  9. Video: Besprechung von Arbeitsblatt 4
  10. Arbeitsblatt 5: Schriftliche Aufgaben
Du kannst Deine Lösungen der schriftlichen Aufgaben
an zirkel@mathematik.uni-stuttgart.de schicken.
Dann erhältst Du eine Musterlösung.

3. Dezimaldarstellung

Verschiedene Darstellungen einer Zahl
  1. Video: Begrüßung
  2. Arbeitsblatt 1: Wiederholung und verschiedene Darstellung von Zahlen
  3. Video: Lösung der Aufgaben 1 und 2, Definition Dezimaldarstellung und Periodenlänge
  4. Arbeitsblatt 2: Dezimaldarstellung
  5. Video: Lösung von Aufgabe 3, Umrechnung periuodischer Dezimaldarstellungen in Brüche
  6. Arbeitsblatt 3: Bruchdarstellung und Dezimaldarstellung
  7. Video: Besprechung von Aufgabe 4, Kriterium für abbrechende Dezimaldarstellung
  8. Arbeitsblatt 4: Periodenlänge
  9. - Video: Besprechung von Arbeitsblatt 4
  10. Arbeitsblatt 5: Schriftliche Aufgaben
Du kannst Deine Lösungen der schriftlichen Aufgaben
an zirkel@mathematik.uni-stuttgart.de schicken.
Dann erhältst Du eine Musterlösung.

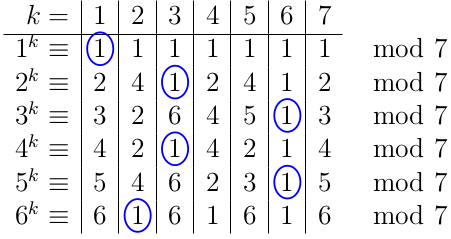
4. Ordnung einer Zahl

Ordnung einer Zahl
  1. Video: Begrüßung
  2. Arbeitsblatt 1: Wiederholung
  3. Video: Lösungen zum Arbeitsblatt 1. Definition der Ordnung einer Zahl. Bitte bereits Arbeitsblatt 2 bereithalten
  4. Arbeitsblatt 2: Ordnung einer Zahl ablesen
  5. Video: Lösungen zum Arbeitsblatt 2. Beweis einer Eigenschaft der Ordnung
  6. Arbeitsblatt 3: Ordnung einer Zahl berechnen
  7. Video: Lösungen zum Arbeitsblatt 3. Zusammenhang mit periodischen Dezimaldarstellungen
  8. Arbeitsblatt 4: Periodenlänge einer Dezimaldarstellunge
  9. - Video: Lösung zum Arbeitsblatt 4. Dezimaldarstellungen mit gerader Periodenlänge
  10. Arbeitsblatt 5: Große Periodenlängen
  11. - Video: Lösungen zum Arbeitsblatt 5 . Dezimaldarstellungen mit gerader Periodenlänge
  12. Arbeitsblatt 6: Schriftliche Aufgaben
Du kannst Deine Lösungen der schriftlichen Aufgaben
an zirkel@mathematik.uni-stuttgart.de schicken.
Dann erhältst Du eine Musterlösung.

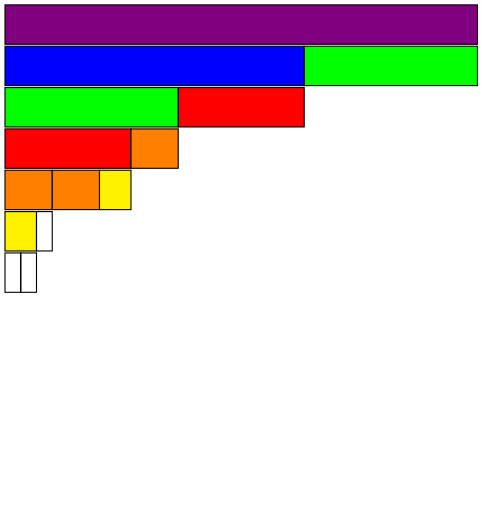
5. Euklidischer Algorithmus

Euklidischer Algorithmus
  1. Video: Begrüßung
  2. Arbeitsblatt 1: Wiederholung
  3. Video: Lösungen zum Arbeitsblatt 1. Größter gemeinsamer Teiler und Teilen mit Rest
  4. Arbeitsblatt 2: Teilen mit Rest
  5. Video: Lösungen zum Arbeitsblatt 2. Euklidischer Algorithmus mit Erklärung
  6. Arbeitsblatt 3: Euklidischer Algorithmus
  7. Video: Lösungen zum Arbeitsblatt 3. Lösung von Kongruenzgleichungen
  8. Arbeitsblatt 4: Kongruenzgleichungen
  9. Video: Lösungen zum Arbeitsblatt 4.
  10. Arbeitsblatt 5: Schriftliche Aufgaben
Du kannst Deine Lösungen der schriftlichen Aufgaben
an zirkel@mathematik.uni-stuttgart.de schicken.
Dann erhältst Du eine Musterlösung.

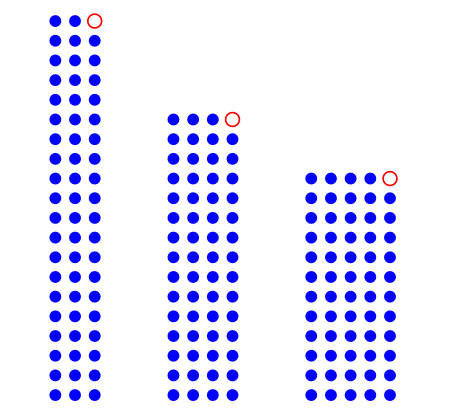
6. Chinesischer Restsatz

Chinesischer Restsatz
  1. Video: Begrüßung
  2. Arbeitsblatt 1: Wiederholung
  3. Video: Lösungen zum Arbeitsblatt 1. Satz über die Lösung von Kongruenzgleichungen
  4. Arbeitsblatt 2: Kongruenzgleichungen
  5. Video: Lösungen zum Arbeitsblatt 2. Der Chinesische Restsatz
  6. Arbeitsblatt 3: Chinesischer Restsatz
  7. Video: Lösungen zum Arbeitsblatt 3. Beweis des Restsatzes und Lösungsmethode
  8. Arbeitsblatt 4: Chinesischer Restsatz
  9. Video: Lösungen zum Arbeitsblatt 4.
  10. Arbeitsblatt 5: Schriftliche Aufgaben
Du kannst Deine Lösungen der schriftlichen Aufgaben
an zirkel@mathematik.uni-stuttgart.de schicken.
Dann erhältst Du eine Musterlösung.

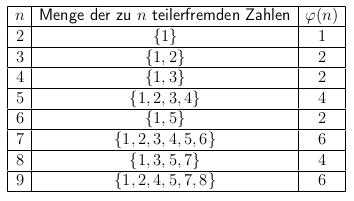
Bonus-Material: Die Eulersche Phi-Funktion

Phi-Funktion
  1. Video: Definition der Phi-Funktion
  2. Bonus-Arbeitsblatt 1: Die Eulersche Phi-Funktion
  3. Video: Lösungen zum Bonus-Arbeitsblatt 1. Formeln zur Berechnung der Phi-Funktion
  4. Bonus-Arbeitsblatt 2: Anwendung der Formeln
  5. Video: Lösungen zum Arbeitsblatt 2. Berechnung der Phi-Funktion für ein Produkt aus Potenzen dreier Primzahlen

© Schülerzirkel Mathematik, Universität Stuttgart, 2021 Copyright BY-NC-SA
Die Materialien des Schülerzirkels stehen unter der der Creative Commons Lizenz BY NC SA

>>>Übersicht über alle online-Kurse im Schülerseminar Mathematik
>>>Hier gibt es allgemeine Informationen zum Schülerseminar Mathematik für Klasse 8-10
>>>Hier geht's zur Übersicht über alle Angebote des Schülerzirkels Mathematik

Zurück zur Homepage von P. Lesky.