Es gibt nichts Praktischeres
als eine gute Theorie.
Immanuel Kant (1724–1804)
Höhere Mathematik 3 (vertieft)
Herzlich willkommen auf der jahrgangsübergreifenden Seite der HM3 (vertieft) für die beiden Stuttgarter Studiengänge Materialwissenschaften und Luft- und Raumfahrttechnik! Hier finden Sie die Vorlesungsunterlagen zum Lernen sowie Klausuren vergangener Jahrgänge zum Trainieren und weitere Materialien wie Lernposter zur Motivation.

Meine Vorlesung fand im WiSe 2021/22 nach drei traumatischen Corona-Semestern wieder in Präsenz statt, live und interaktiv im Hörsaal, direkt und unterhaltsam, und hat mir viel Freude bereitet. Bitte bleiben Sie dabei, Ihre Anwesenheit hilft Ihnen und freut mich, bitte kommen Sie regelmäßig!
Als zusätzliches Angebot, falls jemand mal das Original verpasst, habe hat ich die Vorlesung aufgezeichnet. Das ist nach Präsenz zwar nur das Zweitbeste, doch ich habe mich bemüht, das beste herauszuholen mit der verhandenen Hörsaaltechnik und eigenen Verbesserungen (Kamera, Licht, ...). Meine Vorlesungsvideos finden Sie, ebenfalls als jahrgangsübergreifendes Angebot, in der eigens dafür eingerichteten Ilias-Gruppe: Vorlesungsvideos zur Höheren Mathematik 3 (vertieft) im WiSe 2021/22 bei Prof. Dr. Michael Eisermann
Das HM3-Rundum-Glücklich-Paket: die Vorlesungsfolien eingebettet in ein Lese- und Arbeitsbuch
Wer vieles bringt, wird manchem etwas bringen.
Johann Wolfgang von Goethe (1749–1832),
Faust
Parallel zu meiner aktuellen Vorlesung HM3 stelle ich hier meine Folien zur Verfügung, erprobt und umfassend. Sie sind kein knappes Nachschlageheft, sondern ein umfängliches Lese- und Arbeitsbuch. Wer sie nur hastig durchblättert, wird ihren Umfang abschreckend finden. Wer sich jedoch ernsthaft einarbeitet, wird sie gut nutzen können.
„Danke für das umfassende Skript! Wozu lohnt sich noch die Vorlesung?“
Hierzu urteilte John Hennessy, Präsident der Stanford University, im Interview mit der Wochenzeitung Die Zeit vom 22.03.2016: „Eines ist klar: Die Revolution fällt aus. Das Präsenzstudium bleibt der Normalfall. Wir Menschen brauchen fürs Lernen die persönliche Ansprache, das Mentoring, die Unterstützung." Die fehlende Präsenz und Interaktion während der Corona-Semester bestätigen dies schmerzhaft. In der Präsenzlehre verhallt die Botschaft leider oft ungehört.
Entscheiden Sie weise, studieren Sie ernsthaft, nutzen Sie Ihre Vorlesung!
- Die Vorlesung ist gut strukturiert, höchst informativ, oft sogar unterhaltsam. Die Evaluation (Umfrage während des Semesters) ist entsprechend sehr gut, sogar hervorragend für eine Mathematik-Vorlesung in der Grundausbildung für Ingenieur:innen.
- Vorlesung, Übung, Klausur sind bestens aufeinander abgestimmt: Die Vorlesung erklärt, die Übung trainiert, in der Klausur schließlich stellen die Teilnehmer:innen ihr Wissen und Können unter Beweis. Gemeinsam lernt es sich am besten.
- Nach Aussagen aktiver Teilnehmer:innen erleichtert mein Vortrag den Einstieg, bietet lebendige Erklärungen und Interaktion. Dieses Angebot nehmen allzu wenige wahr; die es am nötigsten hätten, bleiben fern.
Nutzen Sie also die Angebote!
- Sicher, ein anspruchsvolles Ingenieurstudium ist anstrengend und zeitintensiv. Andererseits werden Sie hier in der HM3 bestens betreut. Dennoch geht die Mehrheit der Eingeschriebenen nicht zur Vorlesung. Das ist töricht.
- Sicher, in der Vorlesung besteht keine Anwesenheitspflicht. Wer die Inhalte zu anderen Zeiten, an anderen Orten, auf anderen Wegen lernt, darf das gerne tun. Erfahrungsgemäß passiert das selten oder fast nie, es bleibt ein guter Vorsatz für St. Nimmerlein.
- Sicher, einige Studierende lernen lieber alleine nach ihrem eigenen Rhythmus mit Videos, vielleicht mit dem Skript, oder gar mit Büchern. Die meisten hingegen bleiben der Vorlesung fern und investieren auch sonst keinerlei Mühe.
Was lernen Eingeschriebene eigentlich an der Uni, wenn sie nicht hingehen? Herzlich wenig! Erfahrungsgemäß sind ihre Ergebnisse entsprechend katastrophal. Das ist sehr unglücklich, aber nicht zu ändern. Der Absentismus ist eine Krankheit. Ich kann sie leider nicht heilen, nur präzise diagnostizieren. Das ist zutiefst frustrierend.
Falsche Interpretation: „In der Vorlesung wird nur vorgetragen, was im Skript steht.” Wer glaubt, der Besuch der Vorlesung sei überflüssig, begeht einen gravierenden Fehler. Die Vorlesung ist der erste Schritt des gemeinsamen Lernens.
Richtige Interpretation: Das Skript wird hier als zusätzliches Angebot zu Ihrer Unterstützung zur Verfügung gestellt. Es dient zum Vor- und Nacharbeiten, als hilfreiche Fundierung und Vertiefung zu Vorlesung, Übungen und Klausuren.
Leseanleitung. Die Vortragsfolien sind durch blaue Titelbalken leicht zu erkennen.
Ihre durchgängige Anwesenheit und aktive Teilnahme an der Vorlesung und den Übungen ist der erste wichtige Schritt zu Ihrem Erfolg. Unsere gemeinsame Vorlesungszeit ist daher sehr kostbar und mit 55h auch recht knapp.
Die in der Vorlesung ausgeführten Grundlagen und Anwendungen sind der blaue Faden. (Sie lesen richtig: Der rote Faden ist hier uni-stuttgart-blau.) Dieses Grundgerüst ist eingebettet in ein umfangreiches Lese- und Arbeitsbuch: Dem studentischen Wunsche folgend präsentiere ich zusätzliche Beispiele und Aufgaben mit Lösungen, sowie Erläuterungen und Erinnerungen, Ausführungen und Ergänzungen, auch instruktive Rechnungen und manchmal Beweise, und am Ende jedes Kapitels eine prägnante Zusammenfassung der wichtigsten Ergebnisse. Dies folgt der bewährten Erfahrung, dass die Leserin und der Leser leichter eine vorhandene Übung, Erklärung oder Illustration übergehen kann, als eine fehlende selbst (er)finden. Möge es beiden nützen!
Jedes Kapitel entspricht etwa ein bis zwei Vorlesungen. Im Inhaltsverzeichnis geben somit die Überschriften einen recht detaillierten Überblick der vorgestellten Themen und Methoden. Jedes Kapitel endet mit einer Zusammenfassung (gelbe Titelbalken); nachdem Sie das Thema durchgearbeitet und verstanden haben, ist das erfahrungsgemäß eine hilfreiche Gedächtnisstütze. Als zusätzlicher Service sind alle Kapitelzusammenfassungen im letzten Kapitel Z nochmals zusammengestellt.
Beliebte Formate: 1x1 (Bildschirm), 1x2 (Broschüre), 2x2 (Spiralbindung), 2x4 (Adlerauge), derzeit 432 Seiten DIN A4, viele Bilder, unter 70 MByte. Diese Vollversion enthält alles, was das Herz begehrt: mathematische Grundlagen mit hilfreichen Erläuterungen, Erinnerungen und Ergänzungen, dazu über 800 Aufgaben mit schrittweisen Lösungen, Beispiele und Anwendungen, Zusammenfassungen, wirklich alles. Möge es nützen!
„Wie kann ich einzelne Kapitel herunterladen?“
Einzelne Kapitel als kleine Dateien von circa 1-8 MByte je nach Menge der Bilder:
Viele nutzen die Papierversion (etwa vom Kopierlädle) für eigene Notizen und liebevolle Colorierungen. Das Format 2x4 ist übersichtlich, 2x2 bietet mehr Platz. Arbeitsweisen sind individuell verschieden. Wer ohnehin sein Notebook oder Tablet nutzt, kann Bäume retten, als Bonus die Suchfunktion nutzen (Strg-F) und in der 1x1-Version auch die interne Verlinkung. Pro-Tipp: Ein fettgesetztes Stichwort finden Sie mit #Stichwort.
„Hilfe! Ich bin vom Umfang überfordert.“
Der Umfang des Ihnen hier angebotenen Lernmaterials sollte Sie nicht schrecken, sondern freuen: Studierende, die sich mit der Höheren Mathematik eingehend beschäftigen, fragen oft nach weiteren Anwendungen, Beispielen und Aufgaben, manche wünschen sich zudem Erinnerungen und Illustrationen, Ausführungen und Ergänzungen, etc. Ich helfe gerne, soweit dies möglich ist, und konnte über die Jahre viele Anfragen berücksichtigen. Dadurch wuchs natürlich der Umfang des Skripts, das war ja gerade der studentische Wunsch. Andere wollen sich noch nicht damit auseinandersetzen, vielleicht aber später, je nach Bedarf. Die Lösung ist einfach: Das Skript ist eine hilfreiche Unterstüzung und ein gut gemeintes Angebot. Dosieren Sie selbst!
Neben der Vollversion biete ich versuchsweise eine Halbversion, die mit der Axt auf halbe Länge gekürzt wurde, durch Löschung zahlreicher Beispiele und Aufgaben, Erinnerungen und Illustrationen, Ausführungen und Ergänzungen. Formate: 1x1 (Bildschirm), 1x2 (Broschüre), 2x2 (Spiralbindung), 2x4 (Adlerauge), 212 Seiten DIN A4, etwa 46 MByte. Je nach Bedarf der Leser:in ist die Kürzung an manchen Stellen hilfreich, an anderen fehlt es. Wer es unbedingt kurz braucht, kann zum Einstieg die Halbversion nutzen. Wer sich mehr zutraut, nutzt die Vollversion und dosiert selbst.
Vorlesung und Übungen bieten eine breite Einführung und tragfähige Grundlage. Wenn Sie ein Thema vertiefen wollen, schauen Sie bitte in ein erprobtes Lehrbuch, weiterführende Literatur (siehe Webseite der laufenden Vorlesung), oder wenden Sie sich an die freundlichen Mathematiker:innen Ihres Vertrauens.
Beispieldaten zum Nachrechnen und Experimentieren
- Irrfahrt.ods: Tabellen zu Wärmeleitung und Wahrscheinlichkeiten
- Wuerfeln.ods: Tabelle zum Beispiel Würfeln bis die Eins kommt (T425-28)
- Konfidenz: Konfidenzintervalle interaktiv spielen und erproben (W201-12)
- Venus Express: Daten zur Frage Wieviel Treibstoff ist noch im Tank? (W221-28)
Empfehlenswerte Lehr-und-Lern-Videos. Caution: You will get carried away!
Grant Sanderson erklärt auf 3blue1brown tiefe Mathematik mit wunderschön animierten Graphiken. Sie üben hier nicht rechnen, sondern verstehen! Ich ergänze dies mit weiteren Videos von Edmund Weitz, Burkard Polster auf Mathologer, Henry Reich auf Minutephysics, Michael Stevens auf Vsauce, und einiger weiterer Autoren.
-
Kapitel A-D: Integration
3blue1brown: Hauptsatz der Differential- und Integralrechnung (HDI).
3blue1brown: Wie hängen Steigung und Fläche zusammen?
3blue1brown: Der Flächeninhalt der Sphäre.
Vsauce: The Napkin Ring Problem.
-
Kapitel E-H: Integralsätze
3blue1brown: Divergenz und Rotation: die Sprache der Vektorfelder.
3blue1brown: Komplexe Nullstellensuche... mit Farben!
3blue1brown: Visualisierung der Riemann-Zeta-Funktion.
-
Kapitel I-L: Fourier und Laplace
Mathologer: Epizykel und Fourier-Reihen.
3blue1brown: Fourier-Analyse und Fourier-Reihen.
3blue1brown: Das Basler Problem \(1/1^2 + 1/2^2 + 1/3^2 + 1/4^2 + \ldots = \text{?}\)
-
Kapitel M-P: Gewöhnliche Differentialgleichungen
3blue1brown: Gewöhnliche Differentialgleichungen.
3blue1brown: Die Brachistochrone ausgerechnet.
Vsauce: Die Brachistochrone gebaut und getestet.
Minutephysics: Wie lange fällt man durch die Erde?
-
Resonanz und Dämpfung
The Efficient Engineer: Understanding vibration and resonance.
Practical Engineering: What is a tuned mass damper?
Practical Engineering: Why the Tacoma Narrows Bridge collapsed.
Simon Whistler Sideprojects: Tacoma Narrows Bridge.
Tacoma Narrows Bridge Collapse. (original footage)
-
In/Stabilität um Fixpunkte
Veritasium: The Bizarre Behavior of Rotating Bodies.
Stand-up Maths: Ellipsoids and the Bizarre Behavior of Rotating Bodies.
Physics Unsimplified: Rigid Body Motion and the Dzhanibekov Effect.
-
Drei-Körper-Problem und Lagrange-Punkte
Scott Manley: What makes Lagrange points specials locations in space?
PBS Space Time: Solving the Three Body Problem
-
Kapitel Q-S: Partielle Differentialgleichungen
3blue1brown: Was sind partielle Differentialgleichungen?
3blue1brown: Wie löst man die Wärmeleitungsgleichung?
3blue1brown: Die Unschärferelation ist nicht nur Physik.
-
Fluiddynamik in voller Pracht und Schönheit
braintruffle: Understanding fluid simulation: microscopic perspective.
braintruffle: Understanding fluid simulation: macroscopic perspective.
-
Kapitel T-W: Wahrscheinlichkeitsrechnung
Veritasium: The Bayesian Trap.
Julia Galef: A visual guide to Bayesian thinking.
Edmund Weitz: Was ist eigentlich Wahrscheinlichkeit?
-
Mathematische Grundlagen:
3blue1brown: Grundlagen der Analysis.
3blue1brown: Taylor-Entwicklung und Reihen.
3blue1brown: Determinante als Fläche und Volumen.
3blue1brown: Eigenvektoren und Eigenwerte.
Mathologer: The truth about \( 1 + 2 + 3 + \ldots = -1/12 \).
-
Unterhaltung mit viel Wow! und Aha!:
Veritasium: The most powerful Computers you've never heard of
Edmund Weitz: Mathematische Eleganz hoch drei (Weihnachtsvideo 2021)
3blue1brown: Kollisionen zählen... mit Pi!
3blue1brown: Der Satz von Borsuk-Ulam.
Mathologer: Secrets of the Nothing Grinder.
Klausurenarchiv der HM3 (vertieft)
Über die Jahre halten wir die Vorlesung reihum im Team (Witt, Semmelmann, Eisermann). Im Hintergrund betreue ich als Modulverantwortlicher durchgängig die HM3 (vertieft) für die Studiengänge Luft- und Raumfahrttechnik und Materialwissenschaft. Auf Wunsch der Studierenden sammeln wir hier Klausuren der letzten Jahrgänge.
Jahrgang 2024/2025 bei Prof. Michael Eisermann
- Klausur vom 26.02.2025: Klausurtext, Lösung
- Scheinklausuren waren dieses Jahr nicht vorgesehen.
Jahrgang 2023/2024 bei Prof. Frederik Witt
- Klausur vom 28.02.2024: Klausurtext, Lösung
- Klausur vom 22.08.2024: Klausurtext, Lösung
- Scheinklausuren waren dieses Jahr nicht vorgesehen.
Jahrgang 2022/2023 bei Prof. Uwe Semmelmann
- Klausur vom 01.03.2023: Klausurtext, Lösung
- Klausur vom 24.08.2023: Klausurtext, Lösung
- Scheinklausuren waren dieses Jahr nicht vorgesehen.
Jahrgang 2021/2022 bei Prof. Michael Eisermann
- Klausur vom 02.03.2022: Klausurtext, Lösung
- Klausur vom 25.08.2022: Klausurtext, Lösung
- Scheinklausuren waren dieses Jahr nicht möglich.
Jahrgang 2021/2022 bei Prof. Andreas Kollross
- Klausur vom 03.03.2021: Klausurtext, Lösung
- Klausur vom 26.08.2021: Klausurtext, Lösung
- Scheinklausuren waren dieses Jahr nicht möglich.
Jahrgang 2019/2020 bei Prof. Frederik Witt
- Klausur vom 26.02.2020: Klausurtext, Lösung
- Klausur vom 20.08.2020: Klausurtext, Lösung
- Scheinklausur vom 07.12.2019: Klausurtext, Lösung
- Nachklausur vom 04.02.2019: Klausurtext, Lösung
- Scheinklausur vom 25.01.2020: Klausurtext, Lösung
- Nachklausur vom 04.02.2020: Klausurtext, Lösung
Jahrgang 2018/19 bei Prof. Uwe Semmelmann
- Klausur vom 27.02.2019: Klausurtext, Lösung
- Klausur vom 05.09.2019: Klausurtext, Lösung
Jahrgang 2017/18 bei Prof. Michael Eisermann
- Klausur vom 28.02.2018: Klausurtext, Lösung
- Klausur vom 06.09.2018: Klausurtext, Lösung
- Scheinklausur vom 02.12.2017: Klausurtext, Lösung
- Scheinklausur vom 20.01.2018: Klausurtext, Lösung
- Scheinklausur vom 06.02.2018: Klausurtext, Lösung
Jahrgang 2016/17 bei Prof. Frederik Witt
- Klausur vom 01.03.2017: Klausurtext, Lösung
- Klausur vom 07.09.2017: Klausurtext, Lösung
- Scheinklausur vom 10.12.2016: Klausurtext, Lösung
- Scheinklausur vom 31.01.2017: Klausurtext, Lösung
Jahrgang 2015/16 bei Prof. Michael Eisermann
- Klausur vom 24.02.2016: Klausurtext, Lösung
- Klausur vom 01.09.2016: Klausurtext, Lösung
- Scheinklausur vom 28.11.2015: Klausurtext, Lösung
- Scheinklausur vom 16.01.2016: Klausurtext, Lösung
- Scheinklausur vom 05.02.2016: Klausurtext, Lösung
Weitere Abschlussklausuren aus der Höheren Mathematik für andere Studiengänge finden Sie im gemeinsamen Klausurenarchiv der Höheren Mathematik in Stuttgart.
Lernposter zur Mathematik
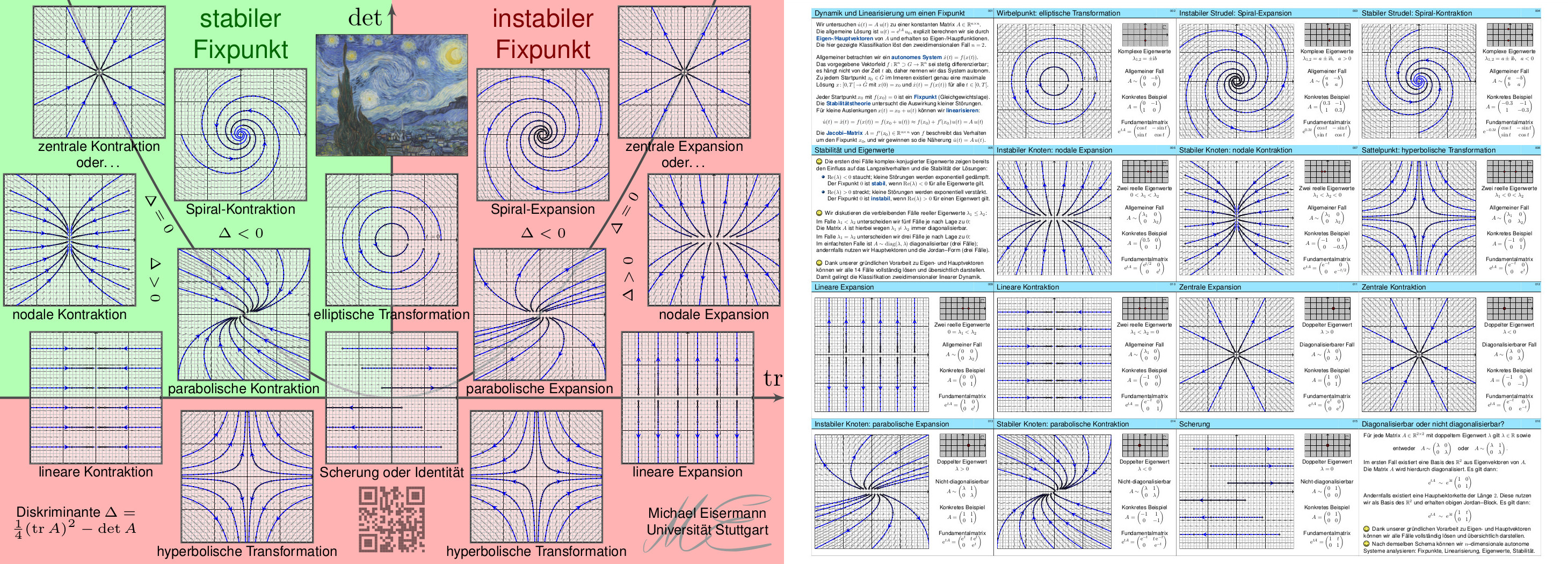
Das lange Warten hat sich gelohnt, die Sehnsucht wird erfüllt, endlich ist es da: Das epische Poster zur zweidimensionalen Dynamik um einen Fixpunkt. Jetzt im Fanshop!
Sie sehen hier unser erstes Lernposter, eben noch in der Vorlesung, jetzt frisch aus der Druckerei: schöne Mathematik zum günstigen Preis! Ab sofort ist dieses Kleinod im Fanshop erhältlich. Fragen Sie die freundlichen Mathematiker:innen Ihres Vertrauens!
„Wow, das ist phantastisch! Wozu ist dieses Poster gut?“ Es gibt viele gute Gründe...
Spannender Inhalt: Das Poster zeigt die Dynamik zweidimensionaler Systeme um einen Fixpunkt, wie in der Vorlesung erklärt und überall im Leben anzutreffen. Weitere faszinierende Mathematik wie Differentialgleichungen, Integration, Fourier- und Laplace-Transformation, usw. wurden schon nachgefragt und sollen folgen. (Alles wird... gut! Es fragt sich nur... wann?)
Motivierende Darstellung: Dieses Poster ist ein Fest für die Sinne, optisch ansprechend und haptisch angenehm, zudem geruchsneutral. Es motiviert zur Prüfungsvorbereitung, die Vorderseite bietet den Überblick (wie oben abgebildet), die Rückseite diskutiert alle gezeigten Fälle explizit mit Zahlenbeispielen. (Ein Klick aufs Bild zeigt eine Vergößerung.)
Gilt ewig: Nur die Mathematik bietet Garantie auf immer und ewig! Alle unsere Sätze sind eternity-proof dank quelloffener nachvollziehbarer Beweise.
Perfekt verarbeitet: Hochwertiger Druck auf DIN A3 Bilderdruckpapier (250g/m2), beidseitig beschichtet, betörende Optik, edle Haptik, robust und abwischbar. Als kostenlosen Bonus geben wir obendrein 100 Jahre Garantie gegen Durchrosten.
Schmückt die Wand: Dieses Poster ziert jede Wohnheimwand und jedes WG-Zimmer. Es vertreibt schlechte Träume und sorgt für gesunden Schlaf unter Sternenhimmel.
Bringt Glück: Dieses Poster bringt Glück. Ich glaube zwar nicht an esoterischen Humbug, aber es soll auch helfen, wenn man nicht daran glaubt.
In der Mensa getestet: Dieses Wunderposter ist bestens als Tischset geeignet. Wir haben es in der Mensa getestet, und das ist kein Witz: Es widersteht Bratensoße und Salatdressing. (Die Mensa möchte in Zukunft vielleicht auf DIN-A3-kompatible Tabletts umrüsten, wir werden sehen.) Ob das Poster auch hitzebeständig ist, konnten wir technisch bedingt in der Mensa noch nicht testen.
Vielfältige Einsatzmöglichkeiten: Kaufen Sie gleich zwei Sets für ein romantisches Candle-Light-Dinner. Wenn das Ihr Ziel sein sollte, der Nerd-Faktor ist garantiert!
Wenn Sie weitere Anwendungen finden, sinnige und unsinnige, oder weitere gute Gründe zum Kauf dieses Posters, bitte schreiben Sie eine Notiz und heben sie diese gut auf!
![[banner]](/igt/eiserm/banners20/Campus-Vaihingen-20211021.jpg) Michael Eisermann
Michael Eisermann