Hier gibt es eine Übersicht über die Themen, die als
e-learning-Kurse, als Video-Kurse oder/und als Selbstlern-Skript
verfügbar sind. Die e-learning-Kurse
bestehen jeweils aus mehreren html-Seiten mit Erklärungen und Aufgaben.
Die Video-Kurse starten jeweils mit einem kurzen Einführungsvideo. Danach
wechseln sich Arbeitsblätter mit Video-Sequenzen ab. Bisher gibt
es Kurse zu den Themen
Iteration und Konvergenz,
Graphenthorie,
Zahlentheorie und Kryptographie,
Kegelschnitte,
Logik und Beweise,
Lineare Abbildungen - geometrisch
und analytisch,
Komplexe Zahlen,
Reelle Nullstellen von Polynomen,
Funktionen und
Umkehrfunktionen und
Primzahlen.
Am 7. Mai 2025 (Präsenz) bzw. 9. Mai 2025
(online)
startet das Schülerseminar mit dem Thema
Symmetrien und Gruppen.
Die Einheiten für die online-Teilnahme
werden im Abstand von ungefähr zwei Wochen ins Netz gestellt.
Zu jeder Einheit gibt es schriftliche Aufgaben. Bei Einsendung der
schriftlichen Aufgaben erhältst Du eine Musterlösung. Falls Du
mindestens vier Mal Lösungen einsendest, erhältst Du eine
Teilnahmebescheinigung.
Falls Du Interesse an regelmäßigen kostenlosen
Informationen zum Schülerseminar hast, kannst Du dich
>>> hier anmelden. Bitte "Ich möchte am Schülerseminar
teilnehmen" ankreuzen.
Autor:
P. Lesky.
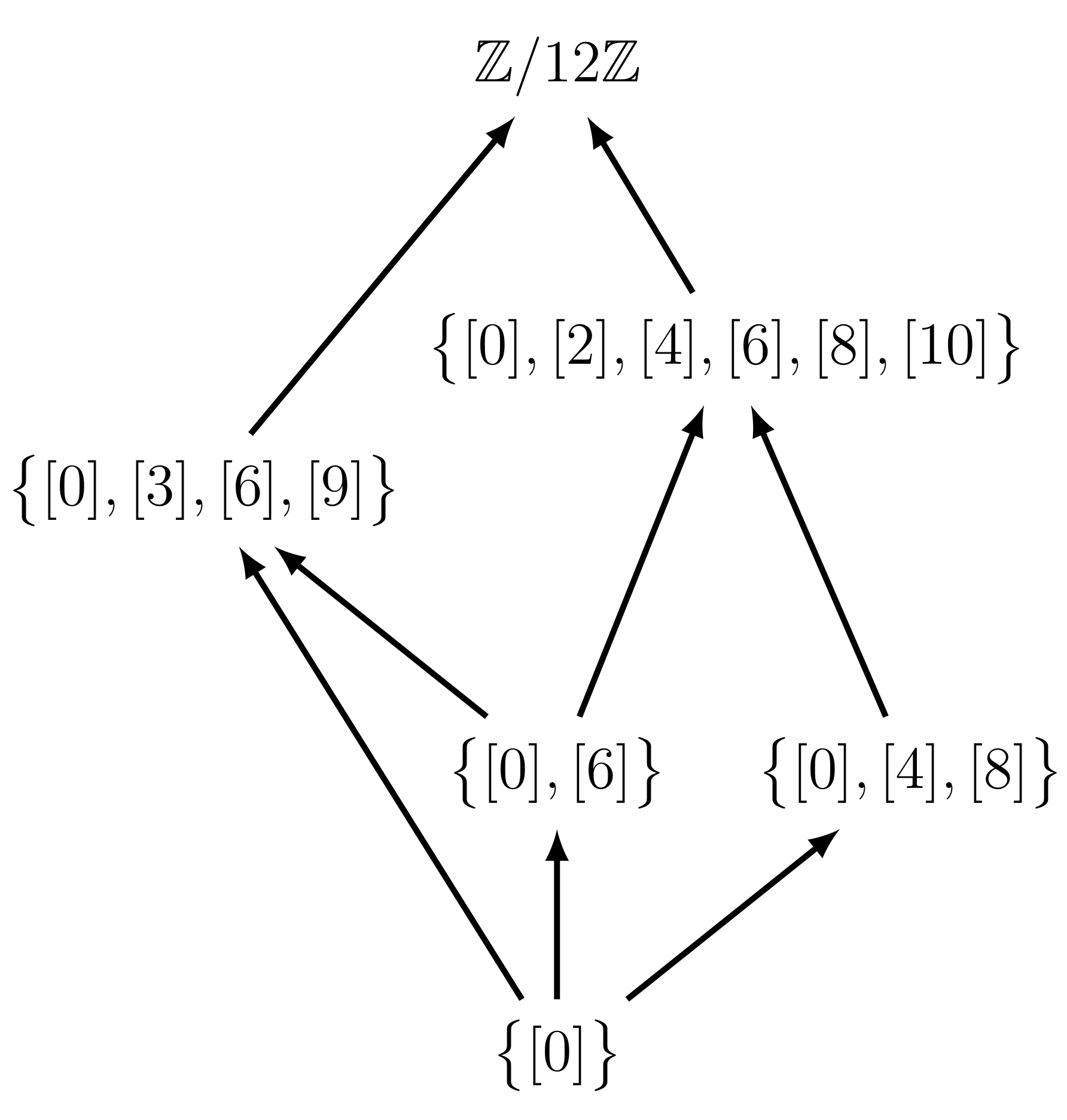
Thema 1, Gruppen: Video-Kurs
Bitte Lösungen zum schriftlichen Aufgabenblatt des 1. Themas bis 24.5.2025 als pdf-Datei einsenden.
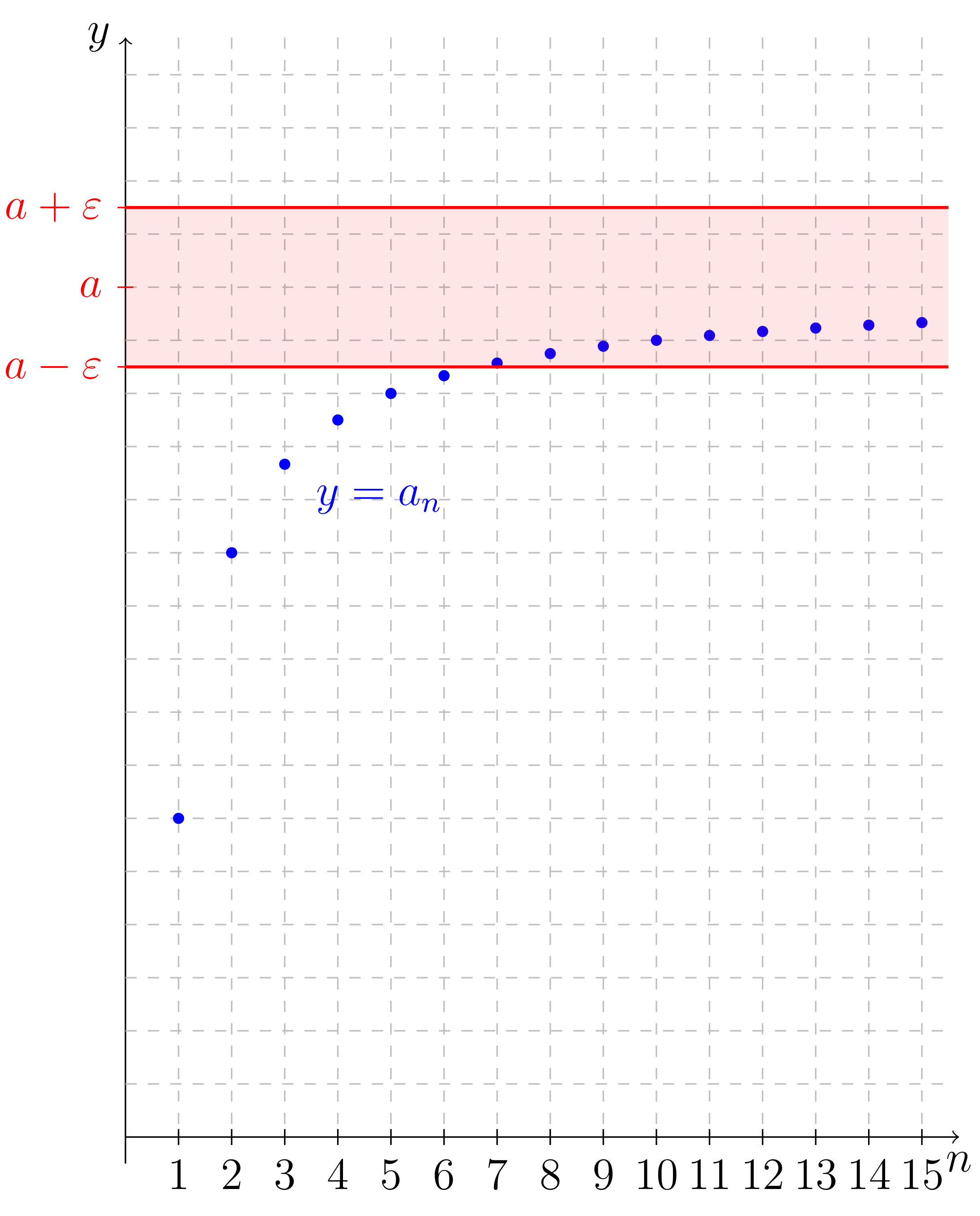
Thema 1, Die Kreiszahl Pi: Video-Kurs und schriftlicher Selbstlern-Kurs
Thema 2, Achill und die Schildkröte: Video-Kurs und schriftlicher Selbstlern-Kurs
Thema 3, Wurzelziehen: Video-Kurs und schriftlicher Selbstlern-Kurs
Thema 4, Rationale und irrationale Zahlen: Video-Kurs und schriftlicher Selbstlern-Kurs
Thema 5, Intervallschachtelung: Video-Kurs und schriftlicher Selbstlern-Kurs
Thema 6, Konvergenz: Video-Kurs und schriftlicher Selbstlern-Kurs
Bitte Lösungen zum schriftlichen Aufgabenblatt des 6. Themas bis 3.4.2025 als pdf-Datei einsenden.
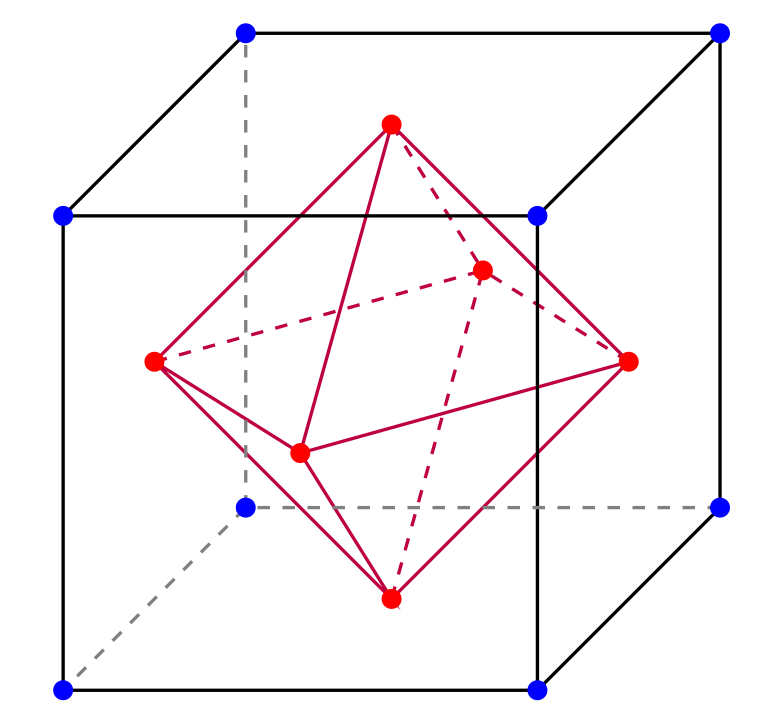
Thema 1: Graphen und Rundwege
Video-Kurs
und schriftlicher Selbstlern-Kurs
Thema 2: Einfache und hamiltonsche Graphen
Video-Kurs
und schriftlicher Selbstlern-Kurs
Thema 3: Hamiltonsche Graphen, Kreise und Bäume
Video-Kurs
und schriftlicher Selbstlern-Kurs
Thema 4: Bäume und bipartite Graphen
Video-Kurs
und schriftlicher Selbstlern-Kurs
Thema 5: Bipartite und plättbare Graphen
Video-Kurs
und schriftlicher Selbstlern-Kurs
Thema 6: Plättbare und nicht plättbare Graphen
Video-Kurs
und schriftlicher Selbstlern-Kurs
Thema 7: Graphen und Polyeder
Video-Kurs
und schriftlicher Selbstlern-Kurs
Neu 2024: Selbstlernskript Zahlentheorie und Kryptographie mit allen Themen, ohne schriftliche Aufgaben.
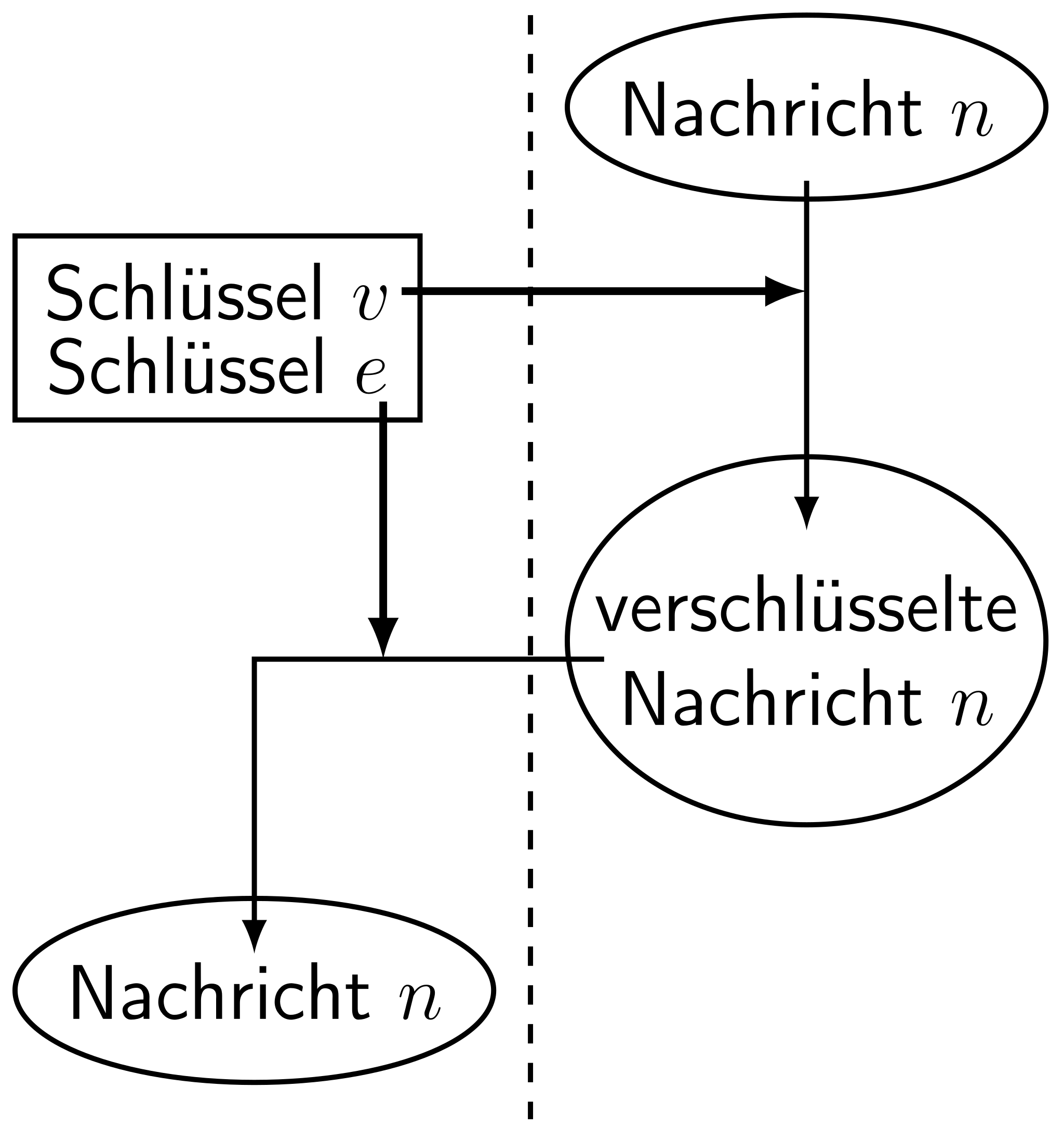
Thema 1, Euklidischer Algorithmus: Video-Kurs,
Thema 2, Diophantische Gleichungen: Video-Kurs,
Thema 3, Kongruenzen:
Video-Kurs
Thema 4, Der Zahlenring: Video-Kurs
Thema 5, Entschlüsselung geheimer Botschaften: Video-Kurs
Thema 6, Kleiner Satz von Fermat:
Video-Kurs,
Thema 7, Asymmetrische Verschlüsselung:
Video-Kurs,
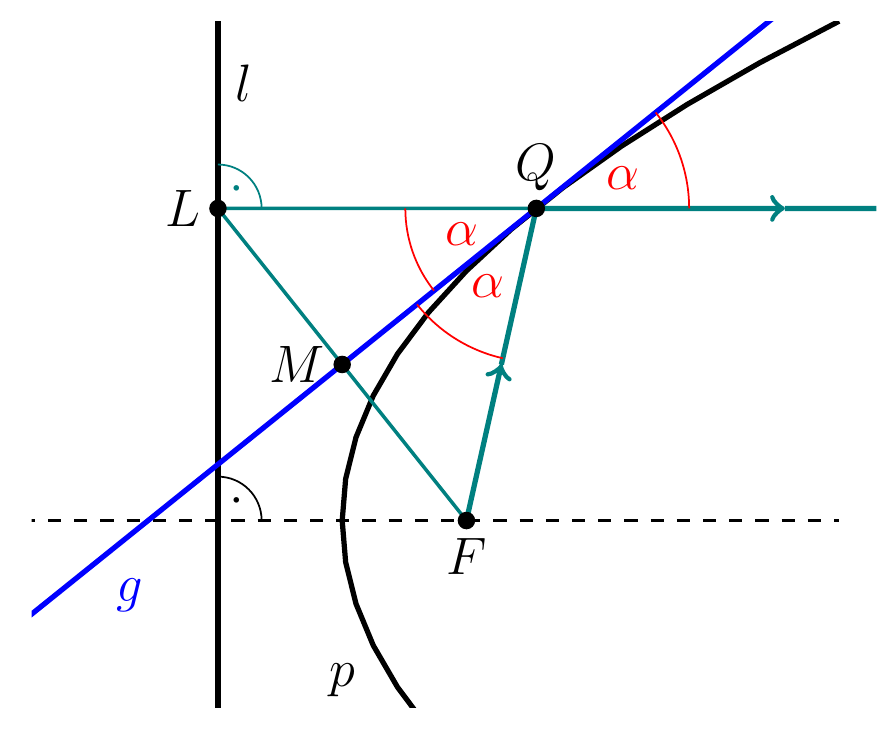
Thema 1, Abstände: Video-Kurs, e-Learning-Kurs
Thema 2, Parabeln: Video-Kurs, e-Learning-Kurs
Thema 3, Parabel und Tangente: Video-Kurs, e-Learning-Kurs
Thema 4, Ellipse: Video-Kurs, e-Learning-Kurs
Thema 5, Ellipse und Tangente: Video-Kurs, e-Learning-Kurs
Thema 6, Hyperbel und Tangente: Video-Kurs, e-Learning-Kurs
Thema 1, Aussagenlogik:
Video-Kurs
Thema 2, Direkter Beweis und Gegenbeispiel:
Video-Kurs
Thema 3, Beweis durch Kontraposition: Video-Kurs
Thema 4, Beweis durch Widerspruch:
Video-Kurs
Thema 5, Vollständige Fallunterscheidung:
Video-Kurs
Thema 6, Vollständige Induktion:
Video-Kurs
Thema 7, Das Invarianzprinzip:
Video-Kurs
Inhalt: Wir untersuchen die Eigenschaften von Ähnlichkeitsabbildungen der Ebene (Streckung, Spiegelung, Drehung) und formulieren Abbildungsvorschriften mit Hilfe von Vektoren und Matrizen.
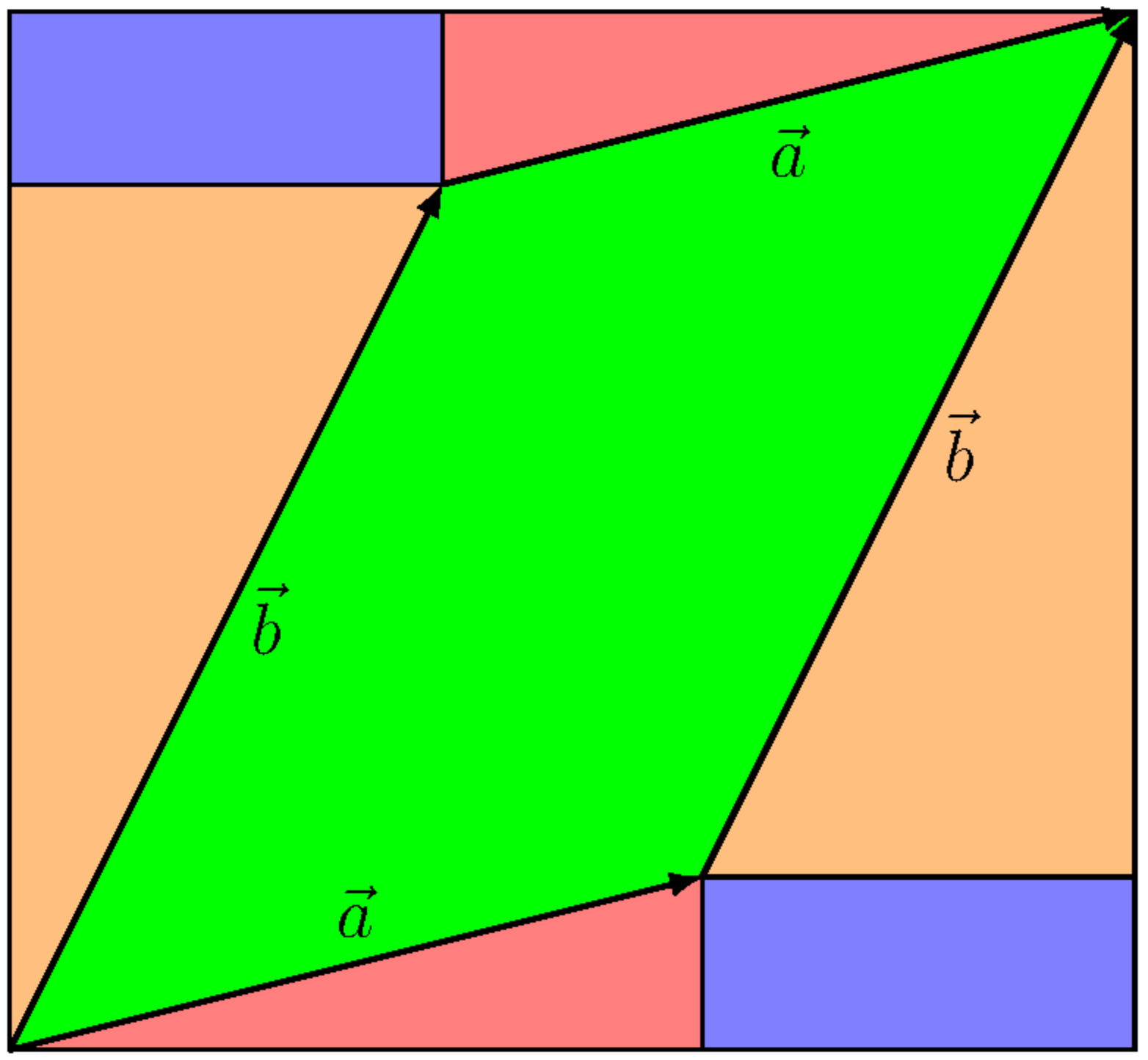
Thema 1, Vektoren: Video-Kurs
Thema 2, Drehungen: Video-Kurs
Thema 3, Geradenspiegelungen: Video-Kurs
Thema 4, Fixpunkte, Fixgeraden, Streckung: Video-Kurs
Thema 5, Geometrische Veranschaulichung: Video-Kurs
Thema 6, Determinanten, Eigenwerte und Eigenvektoren: Video-Kurs
Teaser: Zur Einführung gibt es ein kurzes Video zu komplexen Zahlen.
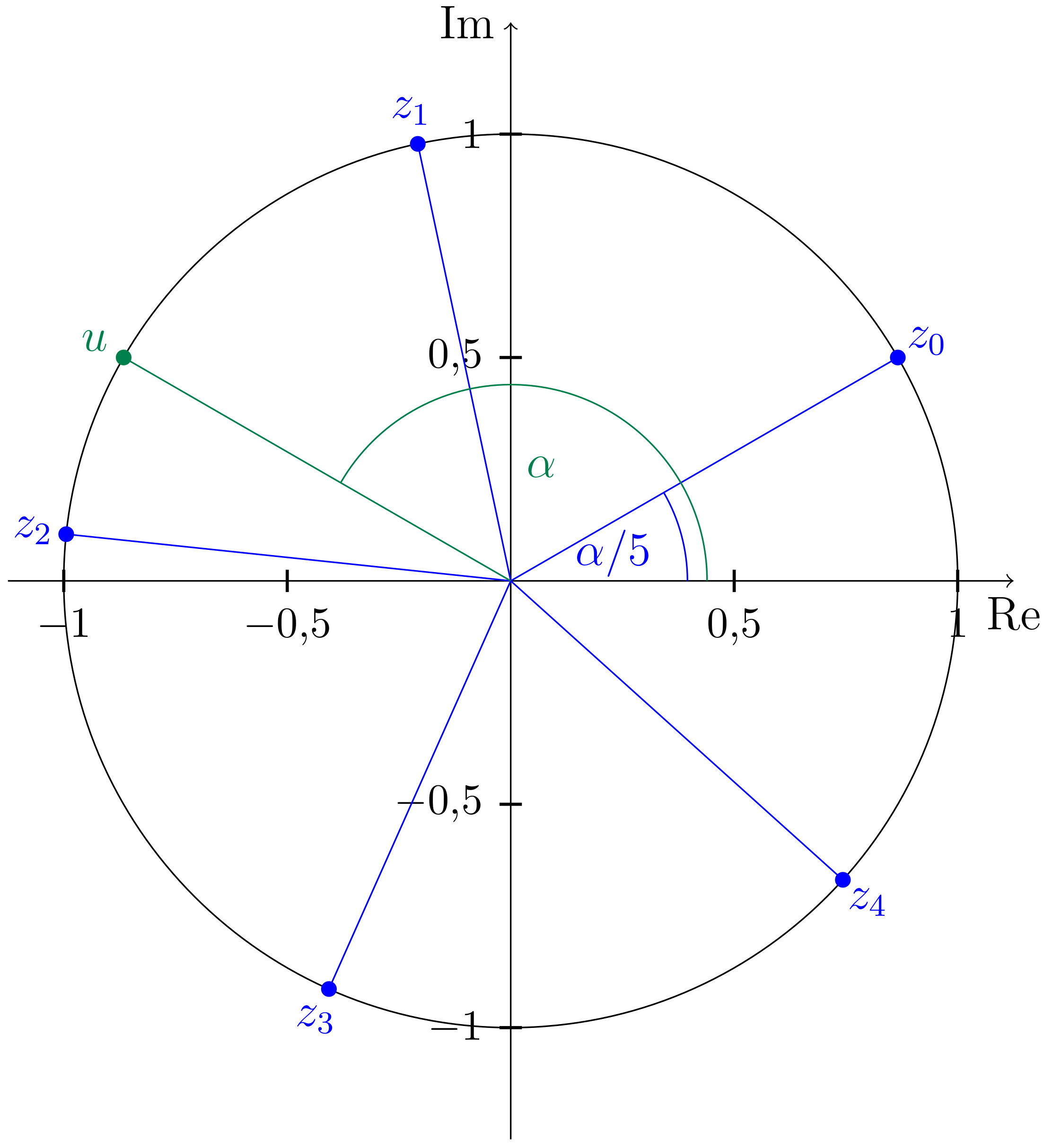
Thema 1, Komplexe Zahlen: Video-Kurs
Thema 2, Die Gaußsche Zahlenebene: Video-Kurs
Thema 3, Sinus und Cosinus: Video-Kurs
Thema 4, Polardarstellung komplexer Zahlen: Video-Kurs
Thema 5, Multiplikation in Polardarstellung: Video-Kurs
Thema 6, Komplexe Wurzeln: Video-Kurs
Thema 1, Quadratische Ergänzung: e-Learning-Kurs, Video-Kurs
Thema 2, Polynomdivision: e-Learning-Kurs, Video-Kurs
Thema 3, Substitution: e-Learning-Kurs, Video-Kurs
Thema 4, Allgemeine Aussagen über Nullstellen: e-Learning-Kurs, Video-Kurs
Thema 5, Gleichungen vierter Ordnung: e-Learning-Kurs, Video-Kurs
Thema 6, Vielfachheit von Nullstellen: e-Learning-Kurs, Video-Kurs
Thema 1, Funktionen: e-Learning-Kurs, Video-Kurs
Thema 2, Monotonie: e-Learning-Kurs, Video-Kurs
Thema 3, Wurzel- und trigonometrische Funktionen: e-Learning-Kurs, Video-Kurs
Thema 4, Arcusfunktionen: e-Learning-Kurs, Video-Kurs
Thema 5, Exponentialfunktionen: e-Learning-Kurs, Video-Kurs
Thema 6, Logarithmusfunktionen: e-Learning-Kurs, Video-Kurs
Thema 1, Primzahlen: e-Learning-Kurs , Video-Kurs
Thema 2, Kongruenzen:
e-Learning-Kurs ,
Video-Kurs
Thema 3, Dezimaldarstellungen:
e-Learning-Kurs ,
Video-Kurs
Thema 4, Ordnung einer Zahl:
e-Learning-Kurs ,
Video-Kurs
Thema 5, Euklidischer Algorithmus: e-Learning-Kurs , Video-Kurs
Thema 6, Chinesischer Restsatz: e-Learning-Kurs , Video-Kurs
Bonus-Material Eulersche Phi-Funktion:
Video-Kurs
© Schülerzirkel Mathematik, Universität Stuttgart,
2021-25 
|
| Die Materialien des Schülerzirkels stehen unter der der Creative Commons Lizenz BY NC SA |
>>>Hier
gibt es weitere Informationen zum Schülerseminar Mathematik
für Klasse 8-10
>>>Hier
geht's zur Übersicht über alle Angebote des Schülerzirkels Mathematik
Zurück zur Homepage von P. Lesky.