



Next: Der Beweis von Satz
Up: Der Hauptsatz der Differentialrechnung
Previous: Das Lemma von Hahn
Contents
Es seien 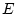 und
und 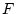 normierte Räume. Für
normierte Räume. Für 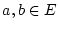 bezeichne
bezeichne
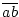 die Strecke
die Strecke
Wir betrachten eine Funktion 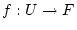 ,
,
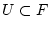 und
wählen die Punkte
und
wählen die Punkte 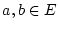 so, daß
so, daß
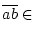
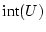 .
.
Satz 3.5.2.1
Die Funktion 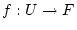 sei in allen
Punkten
sei in allen
Punkten
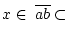
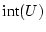 schwach
differenzierbar. Dann gilt
schwach
differenzierbar. Dann gilt
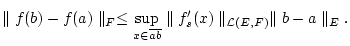 |
(3.5.2.1) |
Der Beweis von Satz 3.5.2.1 folgt im letzten Teil
dieses Abschnittes.
Korollar 3.5.2.2
Ist unter den Voraussetzungen von Satz 3.5.2.1 gilt
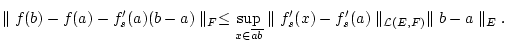 |
(3.5.2.2) |
 Es genügt Satz 3.5.2.1 auf die Funktion
Es genügt Satz 3.5.2.1 auf die Funktion
anzuwenden. Dabei gilt
und (3.5.2.1) geht in (3.5.2.2) über.

2003-09-05
![]() und
und ![]() normierte Räume. Für
normierte Räume. Für ![]() bezeichne
bezeichne
![]() die Strecke
die Strecke
![]() Es genügt Satz 3.5.2.1 auf die Funktion
Es genügt Satz 3.5.2.1 auf die Funktion