



Next: About this document ...
Up: Der Hauptsatz der Differentialrechnung
Previous: Der Beweis von Satz
Contents

 Wir betrachten ein beliebiges lineares stetiges Funktional
Wir betrachten ein beliebiges lineares stetiges Funktional
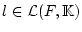 .
Für
.
Für
![$ t\in \, ]-\varepsilon ,1+\varepsilon [ $](img2445.png) setzen wir
Dabei gilt
setzen wir
Dabei gilt
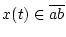 für
für
![$ t\in [0,1] $](img2448.png) sowie
sowie
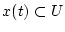 für
für
![$ t\in \, ]-\varepsilon ,1+\varepsilon [ $](img2445.png) mit genügend kleinem
mit genügend kleinem
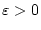 . Wir betrachten die Funktion
. Wir betrachten die Funktion
![% latex2html id marker 31142
$ \psi :[-\varepsilon ,1+\varepsilon ]\to \mathbb{K} $](img2450.png) gegeben
durch
gegeben
durch
Schritt 1: Die Funktion ist für alle
![$ t\in [0,1] $](img2448.png) differenzierbar.
Tatsächlich, aufgrund der Linearität des Funktionals
differenzierbar.
Tatsächlich, aufgrund der Linearität des Funktionals 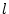 folgt
folgt
Da 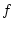 für
für
![$ t\in [0,1] $](img2448.png) im Punkt
im Punkt
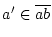 schwach differenzierbar ist, so existiert die Richtungsableitung
Die Stetigkeit von
schwach differenzierbar ist, so existiert die Richtungsableitung
Die Stetigkeit von 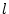 erlaubt uns nun, den Grenzwert
erlaubt uns nun, den Grenzwert
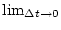 mit dem Funktional
mit dem Funktional  zu vertauschen, woraus die Konvergenz
von
zu vertauschen, woraus die Konvergenz
von
folgt.
Schritt 2: Wir wenden jetzt den Hauptsatz der Differentialrechnung
einer Variablen auf die Funktion  an, welcher die Ungleichung
an, welcher die Ungleichung
liefert. Durch Einsetzen von
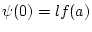 ,
,
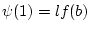 sowie
sowie
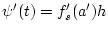 mit
mit 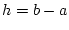 erhält man
erhält man
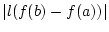 |
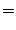 |
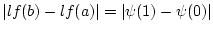 |
(3.5.4.1) |
| |
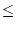 |
![$\displaystyle \sup _{t\in [0,1]}\vert\psi '(t)\vert=\sup _{x\in \overline{ab}}\vert l(f'_{s}(x)h)\vert\notag$](img2470.png) |
(3.5.4.2) |
| |
 |
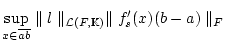 |
(3.5.4.3) |
| |
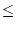 |
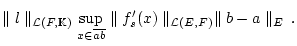 |
(3.5.4.4) |
Schritt 3: Wählt man nun nach dem Lemma von Hahn und Banach
das Funktional
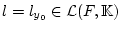 für
für
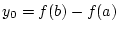 , so daß
, so daß
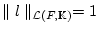 und
und
gilt, dann folgt aus (3.5.4.1) schließlich





Next: About this document ...
Up: Der Hauptsatz der Differentialrechnung
Previous: Der Beweis von Satz
Contents
2003-09-05
![]() differenzierbar.
Tatsächlich, aufgrund der Linearität des Funktionals
differenzierbar.
Tatsächlich, aufgrund der Linearität des Funktionals ![]() folgt
folgt
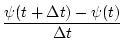
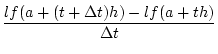
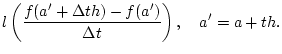
![% latex2html id marker 31167
$\displaystyle Df(a')[h]=\lim _{\Delta t\to 0}\frac{f(a'+\Delta th)-f(a')}{\Delta t}=f'_{s}(a')h.$](img2456.png)
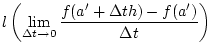
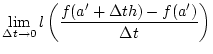
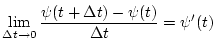
![]() an, welcher die Ungleichung
an, welcher die Ungleichung
![]() für
für
![]() , so daß
, so daß
![]() und
und