



Next: Kompositionen linearer stetiger Operatoren.
Up: Der Raum der stetigen
Previous: Beispiele.
Contents
Definition 3.2.5.1
Wir betrachten zwei normierte lineare Vektorräume
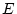
und
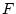
über
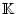
. Mit
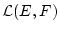
bezeichnen wir
die Menge der stetigen linearen Operatoren
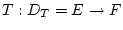
.
Für zwei gegebene Operatoren
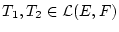 definieren wir deren Summe wiefolgt
Für
definieren wir deren Summe wiefolgt
Für
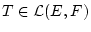 und
und
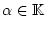 sei weiterhin
sei weiterhin
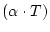 der Operator
Die Abbildungen
der Operator
Die Abbildungen
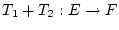 ist dann linear, denn
ist dann linear, denn
für beliebige
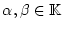 sowie
sowie 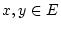 .
.
Aufgabe 3.2.5.2
Zeigen Sie, daß
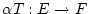
ebenfalls einen linearen Operator
definiert.
Die Abbildung
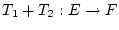 ist stetig, denn als lineare
stetige Operatoren sind
ist stetig, denn als lineare
stetige Operatoren sind 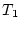 und
und 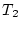 jeweils beschränkt,
womit nach
jeweils beschränkt,
womit nach
der lineare Operator
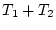 auch beschränkt ist.
auch beschränkt ist.
Aufgabe 3.2.5.3
Zeigen Sie, daß der Operator
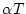
stetig ist.
Damit sind für
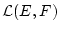 die Operationen der Addition
als auch der Multiplikation mit einem Skalar
definiert.
die Operationen der Addition
als auch der Multiplikation mit einem Skalar
definiert.
Aufgabe 3.2.5.4
Zeigen Sie, daß die Menge
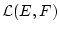
mit den oben gegebenen
Operationen
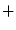
und
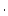
die Struktur eines linearen
Vektorraums besitzt. Das Nullelement
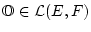
ist dabei derjenige Operator, welcher alle Elemente
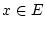
nach
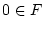
abbildet.
Definition 3.2.5.5
Für Operatoren
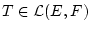
definieren wir die Größe
Da alle Operatoren
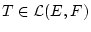 beschränkt sind, so
ist dies eine endliche Größe.
beschränkt sind, so
ist dies eine endliche Größe.
Aufgabe 3.2.5.6
Zeigen Sie, daß
sowie
Satz 3.2.5.7
Das Funktional
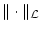 definiert eine
Norm auf dem Raum
definiert eine
Norm auf dem Raum
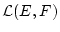 .
.
 Wir verifizieren die Axiome der Norm. Wegen
Wir verifizieren die Axiome der Norm. Wegen
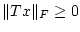 und
und
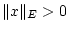 für
für 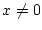 folgt
folgt
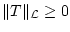 .
Aus
.
Aus
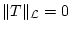 folgt
folgt
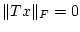 und somit
und somit 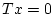 für alle
für alle 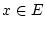 , d.h.
, d.h.
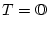 .
.
Die Homogenität von
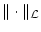 folgt
aus
folgt
aus
Zum Beweis der Dreiecksungleichung merken wir an, daß nach
für jedes
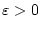 ein solches
ein solches
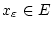 ,
,
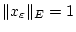 existiert, so daß
Dann gilt
existiert, so daß
Dann gilt
Im Grenzwert
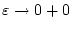 folgt schließlich
folgt schließlich
Satz 3.2.5.8
Ist 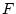 ein Banachraum, so ist
ein Banachraum, so ist
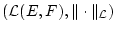 ebenfalls ein Banachraum.
ebenfalls ein Banachraum.
 Wir müssen zeigen, daß jede Cauchy-Folge
Wir müssen zeigen, daß jede Cauchy-Folge
gegen ein Element
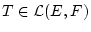 konvergiert.
konvergiert.
Schritt 1: Für die Cauchyfolge
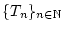 gilt
gilt
Wegen
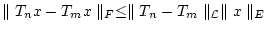 folgt damit
folgt damit
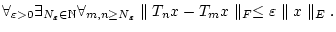 |
(3.2.5.1) |
Also ist für jedes fixierte 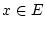 die Folge
die Folge
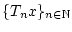 eine Cauchyfolge in
eine Cauchyfolge in 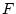 . Aufgrund der Vollständigkeit von
. Aufgrund der Vollständigkeit von 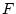 existiert damit ein Grenzwert
existiert damit ein Grenzwert
Schritt 2: Wir betrachten die Abbildung 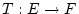 gegeben
durch
gegeben
durch
Wir zeigen, daß 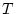 ein linearer Operator ist. Tatsächlich, für
ein linearer Operator ist. Tatsächlich, für
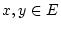 und
und
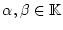 gilt
gilt
Schritt 3: Wir zeigen nun, daß die lineare Abbildung 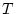 beschränkt und damit stetig ist. Dazu merken wir zunächst an, daß
die Cauchyfolge
beschränkt und damit stetig ist. Dazu merken wir zunächst an, daß
die Cauchyfolge
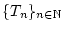 in
in
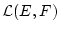 beschränkt ist, d.h.
beschränkt ist, d.h.
für ein geeignetes 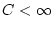 . Aus der Stetigkeit der Norm
. Aus der Stetigkeit der Norm
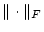 folgt dann
folgt dann
für beliebiges 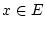 .
.
Schritt 4: Aus den letzten beiden Schritten folgt
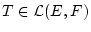 .
Es bleibt zu zeigen, daß
.
Es bleibt zu zeigen, daß
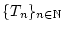 in
in
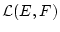 gegen
gegen 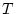 konvergiert. Dazu gehen wir in (3.2.5.1)
für
konvergiert. Dazu gehen wir in (3.2.5.1)
für
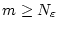 zum Grenzwert
zum Grenzwert
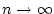 über, woraus man unter der Berücksichtigung der Stetigkeit von
über, woraus man unter der Berücksichtigung der Stetigkeit von
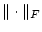 wegen
wegen
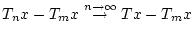 die
Beziehung
die
Beziehung
erhält. Dies impliziert
und damit
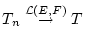 .
.




Next: Kompositionen linearer stetiger Operatoren.
Up: Der Raum der stetigen
Previous: Beispiele.
Contents
2003-09-05
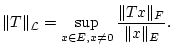
![]() Wir verifizieren die Axiome der Norm. Wegen
Wir verifizieren die Axiome der Norm. Wegen
![]() und
und
![]() für
für ![]() folgt
folgt
![]() .
Aus
.
Aus
![]() folgt
folgt
![]() und somit
und somit ![]() für alle
für alle ![]() , d.h.
, d.h.
![]() .
.
![]() folgt
aus
folgt
aus
![]() Wir müssen zeigen, daß jede Cauchy-Folge
Wir müssen zeigen, daß jede Cauchy-Folge
![]() gilt
gilt![]() gegeben
durch
gegeben
durch
![]() beschränkt und damit stetig ist. Dazu merken wir zunächst an, daß
die Cauchyfolge
beschränkt und damit stetig ist. Dazu merken wir zunächst an, daß
die Cauchyfolge
![]() in
in
![]() beschränkt ist, d.h.
beschränkt ist, d.h.
![]() .
Es bleibt zu zeigen, daß
.
Es bleibt zu zeigen, daß
![]() in
in
![]() gegen
gegen ![]() konvergiert. Dazu gehen wir in (3.2.5.1)
für
konvergiert. Dazu gehen wir in (3.2.5.1)
für
![]() zum Grenzwert
zum Grenzwert
![]() über, woraus man unter der Berücksichtigung der Stetigkeit von
über, woraus man unter der Berücksichtigung der Stetigkeit von
![]() wegen
wegen
![]() die
Beziehung
die
Beziehung