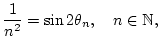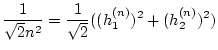Beispiel 3.4.3.2
Wir betrachten die Funktion
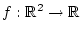
gegeben durch
sowie
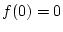
. Es sei
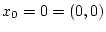
. Für beliebiges
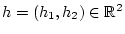
gilt dann
bzw.
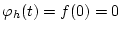
für
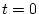
oder
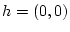
. Folglich gilt
Damit ist
der Nulloperator von
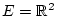
nach
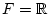
.
Ist die Funktion 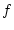 im Punkt
im Punkt
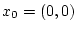 Frechet-differenzierbar,
so gilt
Frechet-differenzierbar,
so gilt
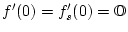 und damit
und damit
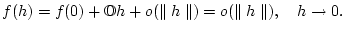 |
(3.4.3.1) |
Wir betrachten nun die Folge
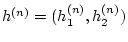
gegeben durch
wobei die Werte
![% latex2html id marker 30879
$ \theta _{n}\in [0,\pi /4] $](img2389.png)
durch die Bedingung
gegeben sind. Dann gilt
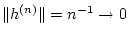
sowie
und folglich
mit
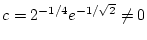
. Die letzte Gleichung
widerspricht der asymptotischen Bedingung (
3.4.3.1).
Damit ist
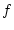
im Punkt
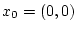
nicht Frechet-differenzierbar.
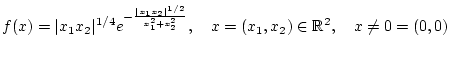
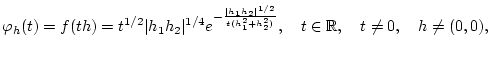
![]() im Punkt
im Punkt
![]() Frechet-differenzierbar,
so gilt
Frechet-differenzierbar,
so gilt
![]() und damit
und damit