Zum Zusammenhang zwischen Frechet- und Richtungsableitung.

Satz 3.4.2.1   Die Funktion $f:U\to F$ sei im Punkt $x_{0}\in$$\mbox {int}(U)$ Frechet-differenzierbar. Dann existiert im Punkt $x_{0}$ für beliebiges $h\in E$ die Richtungsableitung $Df(x_{0})h$ und es gilt

$$Df(x_{0})h=f'(x_{0})h,\quad h\in E.$$ (3.4.2.1)

$\blacktriangleright$ Nach der Definition der Frechet-Ableitung gilt $f(x_{0}+h)=f(x_{0})+f'(x_{0})h+o(\parallel h\parallel )$ für $h\to 0$ und wegen $\Vert th\Vert =\vert t\vert\, \Vert h\Vert$ damit auch

$$f(x_{0}+th)=f(x_{0})+f'(x_{0})th+o(t)$$

für beliebiges fixiertes $h\in E$ und $t\to 0$, $t\in \mathbb{K}$. Daraus folgt sofort

$$Df(x_{0})[h]=\lim _{t\to 0}\frac{f(... ...-f(x_{0})}{t}=f^{\prime }(x_{0})h+\lim _{t\to 0}t^{-1}o(t)=f^{\prime }(x_{0})h.$$

$\blacktriangleleft$

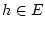Eine wichtige Anmerkung zu diesem Satz besteht darin, daß aus der Existenz der Richtungsableitungen $Df(x_{0})[h]$ für alle $h\in E$ im allgemeinen nicht die Existenz der Frechet-Ableitung 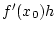$f^{\prime }(x_{0})h$ folgt. Wir illuistrieren dies am folgenden Beispiel:

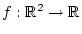
Beispiel 3.4.2.2   Es sei $f:\mathbb{R}^{2}\to \mathbb{R}$ die Funktion

$$f(x)=(x_{1}^{3}+x_{2}^{3})^{1/3},\quad x=(x_{1},x_{2})\in \mathbb{R}^{2},$$

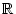
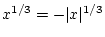
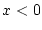
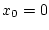
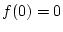
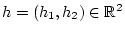
wobei wir hier den reellen Zweig der dritten Wurzel auswählen, d.h. jener welcher die inverse Abbildung zur dritten Potenz auf $\mathbb{R}$ darstellt, also $x^{1/3}=-\vert x\vert^{1/3}$ für $x<0$. Im Punkt $x_{0}=0$ erhält man $f(0)=0$. Für beliebiges $h=(h_{1},h_{2})\in \mathbb{R}^{2}$ gilt

$$\varphi _{h}(t)=((th_{1})^{3}+(th_{2})^{3})^{1/3}=t(h_{1}^{3}+h_{2}^{3})^{1/3}.$$

Daraus folgt

$$Df(0)[h]=\lim _{t\to 0}\frac{\varphi _{h}(t)-\varphi _{h}(0)}{t}=(h_{1}^{3}+h_{2}^{3})^{1/3}.$$

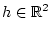
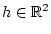
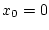
Diese Richtungsableitung existiert für alle $h\in \mathbb{R}^{2}$, der Ausdruck $Df(0)[h]$ ist aber offensichtlich nicht linear in $h\in \mathbb{R}^{2}$. Wäre nun die Funktion $f$ im Punkt $x_{0}=0$ Frechet-differenzierbar, so ist dann nach (3.4.2.1) der Ausdruck $Df(0)[\, \cdot \, ]=f^{\prime }(x_{0})$ unbedingt ein linearer Operator, was zum Widerspruch führt. 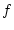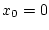Also kann die Frechet-Ableitung von $f$ im Punkt $x_{0}=0$ nicht existieren.