Die Richtungsableitung.

Es seien $E$ und $F$ normierte Räume sowie $U\subset E$. Wir betrachten einen Punkt $x_{0}\in$$\mbox {int}(U)$ und wählen einen Richtungsvektor $h\in E$. Dann gilt $x_{0}+th\in U$ für alle $t\in \mathbb{K}$ mit genügend kleinem Absolutbetrag $\vert t\vert\leq \varepsilon (h)$. Für eine Abbildung $f:U\to F$ setzen wir

$$\varphi _{h}(t)=f(x_{0}+th),\quad t\in \mathbb{K},\quad t\neq 0,\quad \vert t\vert\leq \varepsilon (h).$$

Definition 3.4.1.1   Existiert für gewisses $h\in E$ der Grenzwert

$$Df(x_{0})[h]=\frac{d}{dt}\varphi _{h}(t)\vert _{t=0}=\lim _{t\to 0}\frac{f(x_{0}+th)-f(x_{0})}{t},$$

so nennt man diesen die Richtungsableitung von $f$ im Punkt $x_{0}$ in die Richtung $h$ oder auch die Gateaux-Ableitung von $f$ im Punkt $x_{0}$ in die Richtung $h$.

Der Ausdruck $Df(x_{0})[h]$ ist hier zunächst als ein einheitliches Symbol zu verstehen und nicht als ein Operator $Df(x_{0})$ wirkend auf $h.$ Es zeigt sich aber sofort, daß dieser Ausdruck, sofern er existiert, homogen in der Variablen $h$ ist:

Satz   Die Funktion $f:U\to F$ besitze im Punkt $x_{0}\in$$\mbox {int}(U)$ für gewisses $h\in E$ die Richtungsableitung $Df(x_{0})[h]$. Dann existiert für alle $\alpha \in \mathbb{K}$ die Richtungsableitung $Df(x_{0})[\alpha h]$ und es gilt

$$Df(x_{0})[\alpha h]=\alpha Df(x_{0})[h],\quad \alpha \in \mathbb{K}.$$

$\blacktriangleright$ Ersetzt man $t\in \mathbb{K}$ durch $s=\alpha t\in \mathbb{K}$, so erhält man direkt aus der Definition

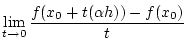$$Df(x_{0})[\alpha h] = \lim _{t\to 0}\frac{f(x_{0}+t(\alpha h))-f(x_{0})}{t}$$

$$= \lim _{s\to 0}\frac{f(x_{0}+sh)-f(x_{0})}{s/\alpha }=\alpha Df(x_{0})[h].$$

$\blacktriangleleft$