



Next: Zur Äquivalenz von Normen
Up: Endlich- und Unendlichdimensionale Vektorräume
Previous: Normierte Vektorräume.
Contents
Eine endliche Familie von gegebenen Vektoren
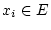 ,
,
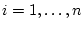 heißt linear unabhängig wenn die Identität
heißt linear unabhängig wenn die Identität
ausschließlich für die Skalare
erfüllt ist. Gibt es eine endliche größte Anzahl von linear unabhängigen
Vektoren, die sich in einem linearen Vektorraum 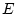 finden lassen,
so nennt man diese Anzahl
finden lassen,
so nennt man diese Anzahl 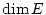 die Dimension von
die Dimension von 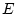 .
Beispiele für endlichdimensionale Banachräume sind z.B.
.
Beispiele für endlichdimensionale Banachräume sind z.B.
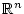 o
o
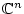 mit der Euklidschen Norm
mit der Euklidschen Norm
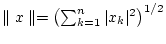 .
Gibt es beliebig große Familien linear unabhängiger Vektoren aus
.
Gibt es beliebig große Familien linear unabhängiger Vektoren aus 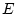 ,
so nennt man
,
so nennt man 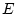 unendlichdimensional und schreibt
unendlichdimensional und schreibt
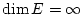 .
.
Wir erinnern daran, daß
![% latex2html id marker 28542
$ C([a,b],\mathbb{K}) $](img1802.png) den Raum der stetigen
den Raum der stetigen
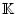 -wertigen Funktionen auf dem Intervall
-wertigen Funktionen auf dem Intervall ![$ [a,b] $](img87.png) bezeichnet. In Abschnitt 2.15 des Skriptes Analysis 1 haben wir gezeigt,
daß
bezeichnet. In Abschnitt 2.15 des Skriptes Analysis 1 haben wir gezeigt,
daß
![$ \parallel f\parallel _{C}=\max _{x\in [a,b]}\vert f(x)\vert $](img1804.png) eine
Norm auf
eine
Norm auf
![% latex2html id marker 28550
$ C([a,b],\mathbb{R}) $](img1805.png) definiert und daß
definiert und daß
![% latex2html id marker 28552
$ C([a,b],\mathbb{R}) $](img1806.png) bezüglich dieser Norm vollständig ist.
bezüglich dieser Norm vollständig ist.
Lemma 3.1.2.1
Es sei
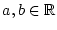 und
und 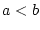 . Dann gilt
. Dann gilt
![% latex2html id marker 28564
$ \dim C([a,b],\mathbb{R})=\infty $](img1809.png) .
.
 Wir betrachten das Intervall
Wir betrachten das Intervall
![$ [a,b]=[0,1] $](img1688.png) , der allgemeine Fall
folgt dann durch eine affine Koordinatentransformation. Wir setzen
, der allgemeine Fall
folgt dann durch eine affine Koordinatentransformation. Wir setzen
![$ x_{n}=n^{-1}\in [0,1] $](img1810.png) für
für
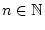 . Wir betrachten
folgende Funktionen
. Wir betrachten
folgende Funktionen
All diese Funktionen sind auf dem Intervall ![$ [0,1] $](img1696.png) stetig als
auch paarweise disjunkt getragen, d.h.
stetig als
auch paarweise disjunkt getragen, d.h.
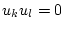 für
für 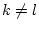 .
Desweiteren gilt
Deshalb nimmt eine jede Linearkombination
der Vektorenfamilie
.
Desweiteren gilt
Deshalb nimmt eine jede Linearkombination
der Vektorenfamilie
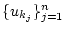 in den Punkten
in den Punkten
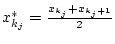 die Werte
die Werte
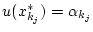 an. Damit gilt
an. Damit gilt 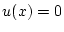 für alle
für alle
![$ x\in [0,1] $](img1712.png) , d.h.
, d.h. 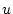 ist das Nullelement in
ist das Nullelement in
![% latex2html id marker 28616
$ C([0,1],\mathbb{R}) $](img1829.png) , genau dann wenn
, genau dann wenn
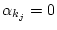 für
für
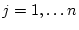 . Damit ist eine beliebige
Vektorenfamilie
. Damit ist eine beliebige
Vektorenfamilie
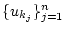 linear unabhängig;
es gibt also beliebig viele linear unabhängige Vektoren in
linear unabhängig;
es gibt also beliebig viele linear unabhängige Vektoren in
![% latex2html id marker 28624
$ C([0,1],\mathbb{R}) $](img1832.png) .
.





Next: Zur Äquivalenz von Normen
Up: Endlich- und Unendlichdimensionale Vektorräume
Previous: Normierte Vektorräume.
Contents
2003-09-05
![]() ,
,
![]() heißt linear unabhängig wenn die Identität
heißt linear unabhängig wenn die Identität
![]() den Raum der stetigen
den Raum der stetigen
![]() -wertigen Funktionen auf dem Intervall
-wertigen Funktionen auf dem Intervall ![]() bezeichnet. In Abschnitt 2.15 des Skriptes Analysis 1 haben wir gezeigt,
daß
bezeichnet. In Abschnitt 2.15 des Skriptes Analysis 1 haben wir gezeigt,
daß
![]() eine
Norm auf
eine
Norm auf
![]() definiert und daß
definiert und daß
![]() bezüglich dieser Norm vollständig ist.
bezüglich dieser Norm vollständig ist.
![]() Wir betrachten das Intervall
Wir betrachten das Intervall
![]() , der allgemeine Fall
folgt dann durch eine affine Koordinatentransformation. Wir setzen
, der allgemeine Fall
folgt dann durch eine affine Koordinatentransformation. Wir setzen
![]() für
für
![]() . Wir betrachten
folgende Funktionen
. Wir betrachten
folgende Funktionen