|
|
 |
Der Durchstoßpunkt Sg einer Geraden g
durch die Bildtafel
 heißt
Spurpunkt von g.
heißt
Spurpunkt von g. |
|
| Bilder paralleler Geraden sind im Allgemeinen nicht
parallel. |
|
Beispiel: jede Gerade senkrecht zur
Bildtafel wird auf eine Gerade durch den Hauptpunkt H
abgebildet.
[ Lässt man einen Punkt auf einer solchen Geraden ins Unendliche
weg laufen, so nähert sich seine Verbindungsgerade mit dem Augpunkt
der Geraden OH an! ] |
| |
|
Geraden senkrecht zur Bildtafel heißen
Tiefenlinien. |
| |
Allgemein gilt:
Die Bilder der Geraden einer Parallelschar sind entweder wieder parallel
oder laufen durch einen gemeinsamen Punkt:
den
Fluchtpunkt der Parallelschar.
|
|
Bilder paraller Geraden g1
, g2 sind dann ( und nur dann ) parallel, wenn g1
, g2 parallel zur Bildtafel verlaufen.
Fluchtpunkt der Tiefenlinien ist der Hauptpunkt. |
| |
|
Fluchtpunkte kann man sehr bequem zur Konstruktion der Bilder einer
Schar paralleler Geraden ausnutzen!
|
|
Man erhält den Fluchtpunkt einer Parallelschar
als Spurpunkt der Parallelen durch den Augpunkt.
( Konstruktion im Grundriss! ) |

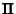 heißt
Spurpunkt von g.
heißt
Spurpunkt von g.