Es gibt nichts Praktischeres
als eine gute Theorie.
Immanuel Kant (1724–1804)
Höhere Mathematik 3 (vertieft)
Vorlesung im Wintersemester 2024/25.
Dozent: Michael Eisermann.
Assistenten: Friederike Stoll,
Ivan Solonenko.
Wir nutzen die Lernplattform Ilias. Alle aktuellen Informationen zu Ihrer HM3, Lehrmaterial, Forum, Termine, etc. finden Sie in unserem liebevoll gestalteten Ilias-Kurs.
Fragen? Für all Ihre Fragen, organisatorisch oder inhaltlich, wenden Sie sich bitte an Herrn Solonenko oder Frau Stoll oder mich. Rückmeldungen? Wir freuen uns über Ihre Anregungen, ehrliches Lob und konstruktive Kritik. Bitte lassen Sie uns wissen, wie Ihnen die Veranstaltung gefällt, wie Sie mit dem Stoff zurecht kommen, und was sich verbessern lässt. Ihr Studium ist wertvoll, nutzen und wertschätzen Sie es, engagieren Sie sich!
Als Einstimmung: Die Begrüßung in den ersten vier Minuten meiner Vorlesung 2021.

Auf dieser ergänzenden, öffentlichen Webseite finden Sie:
- Unterlagen: Meine Vorlesungsfolien zur HM3
- Fromme Worte zu Zielsetzung und Literatur
- Tipps zu Wiederholung, Training, Vorbereitung
- Vorlesungstermine mit Inhaltsangabe
Aktuelles
Bitte schreiben Sie sich möglichst frühzeitig über C@mpus in unseren Ilias-Kurs ein. Dort finden Sie alle aktuellen Informationen dieses Semesters.
Der Gerechte muss viel leiden.
Psalm 34:19
Lernposter zur Motivation
Urlaubsgrüße von Teilnehmer:innen

Drei Teilnehmer sind nach der Vorlesung 2017/18 nach San Francisco gereist, um die Rechnungen vor Ort zu überprüfen. "Wir wollten eigentlich Urlaub machen, aber Ihre Vorlesung hat uns bis ans andere Ende der Welt verfolgt. Viele Grüße aus Kalifornien!"
Praktikumsgrüße aus Berlin

Vielen Teilnehmer:innen gefiel das überraschende HM3-Urlaubsphoto aus San Francisco. Ein freundlicher Einsender hat unsere Sammlung "HM3 around the world" im Frühjahr 2019 um ein zweites Photo erweitert, diesmal nicht aus dem Urlaub, sondern aus dem Praktikum.
"Um Ihre Sammlung HM3 around the world zu ergänzen, habe ich ein Foto mit Ihrem Skript und der praktischen Anwendung angehängt. Viele Grüße und bis zur Spacenight!"
Vielen Dank! Ich bin sehr gerührt. Mein Wirken scheint langfristig doch Spuren hinterlassen zu haben.
Two is a party, three is a crowd? Ich frage mich, ob wir hier vielleicht den Anfang einer HM3-Gallerie sehen... Auch über weitere Einsendungen würde ich mich sehr freuen!

Die Idee solcher Photogrüße erinnert an den Gartenzwerg auf Weltreise aus dem Film Die fabelhafte Welt der Amélie (2001). Hier ist es etwas leichter: Das HM3-Skript liegt elektronisch vor und kann sich an jedem Ort der Welt materialisieren. Aficionados tragen immer eine Kopie als Glückbringer bei sich. Don't leave home without it!
Zielsetzung
Die Vorlesung HM3 baut auf der HM1&2 auf und führt diese fort mit folgendem Ziel:
- Die Studierenden verfügen über grundlegende Kenntnisse der mehrdimensionalen Integralrechnung, Fourier-Reihen und Integraltransformationen, gewöhnliche und partielle Differentialgleichungen, sowie Stochastik.
- Sie sind in der Lage, die behandelten Methoden selbstständig, sicher, kritisch, korrekt und kreativ anzuwenden.
- Sie besitzen die mathematische Grundlage für das Verständnis quantitativer Modelle aus den Ingenieurwissenschaften.
- Sie können sich mit Spezialisten aus dem ingenieur- und naturwissenschaftlichen Umfeld über die benutzten mathematischen Methoden verständigen.
Aus dieser ambitionierten Zielsetzung ergibt sich die Vorgehensweise:
- Selbstständig: Es geht nicht nur um Auswendiglernen,
sondern um Verstehen und unabhängige Urteilsfähigkeit. - Sicher: Es geht nicht nur um Intuition oder Spekulieren,
sondern um nachvollziehbare Argumente und Rechnungen. - Kritisch: Es geht nicht nur um Glauben oder (Auto)Suggestion,
sondern um (selbst)kritische Fragen und sorgfältige Antworten. - Korrekt: Sie beherrschen Definitionen, Sätze, Methoden, Proben.
Gegenbeispiele zeigen Fehlerquellen, die es zu vermeiden gilt. - Kreativ: Es geht nicht nur um fertige Rezepte,
sondern um eigenständige Anwendung.
Der Weg ist lang, doch das Ziel ist hehr! Es geht nur mit Fleiß und Disziplin.
Il dépend de celui qui passe
Que je sois tombe ou trésor
Que je parle ou me taise
Ceci ne tient qu'à toi
Ami n'entre pas sans désir
Paul Valéry (1871–1945)
Fragen und Antworten zur Vorlesung
Half the money I spend on advertising is wasted;
the trouble is I don't know which half.
John Wanamaker (1838–1922)
„Was ist Höhere Mathematik?“
Höhere Mathematik bezeichnet – insbesondere an technischen Hochschulen – jene Teilgebiete der Mathematik, die als mathematische Grundlagen in den ingenieur- und naturwissenschaftlichen Studiengängen gelehrt werden. Der Komparativ 'höher' bezieht sich hierbei auf die Schulmathematik, analog zum Vergleich Schule und Hochschule. Im Gegensatz zu den tiefer gehenden Inhalten des Mathematikstudiums liegt hier die Betonung weniger auf der zugrundeliegenden Theorie (Definitionen, Sätze, Beweise), sondern mehr auf der praktischen Anwendung (Beispiele, Sätze, Rechentechniken).
„Lohnt sich die Mühe?“
Die Erfahrungen Ihrer Studiengänge zeigen ganz klar: Ja!
Die Höhere Mathematik steht aus gutem Grund am Anfang Ihres Ingenieurstudiums, denn die hier behandelten mathematischen Methoden benötigen Sie überall, sie bilden die handwerkliche Grundlage, zunächst für Ihr Studium, später auch im Beruf: Je nach Vertiefung benötigen Sie von manchen Techniken noch wesentlich mehr, z.B. Numerik von Differentialgleihungen, auch darauf sollen Sie sich hier bereits vorbereiten.
„Wann soll ich anfangen?“
Jetzt!
Die Erfahrungen der letzten Jahre zeigen, dass viele Studierende anfangs noch zögern, die nötige Zeit und Ernsthaftigkeit in solide Grundlagen zu investieren. Ohne das nötige mathematische Werkzeug werden Verständnis und Anwendung unnötig erschwert, oft gar unmöglich, sie vergeuden ihre Chancen und verlieren wertvolle Zeit. Vertrauen Sie den vorliegenden Erfahrungen machen Sie es richtig: Investieren Sie von Anfang an die nötige Zeit in Ihre Ausbildung. Dazu gehört als harter Kern auch die Mathematik.
„Ich will Ingenieur:in werden. Wozu brauche ich Mathematik?“
Mathematik ist Grundlage und Werkzeug aller modernen Technologie.
Hochtechnologie ist immer auch mathematische Technologie.
Alle hochqualifizierten Tätigkeiten zielen auf Verständnis und Beherrschung komplexer Zusammenhänge. Hierzu benötigen sie neben Empirie auch Theorie, quantitative Modelle und sorgfältige Planung. Diese beruhen im Wesentlichen auf Mathematik. Der Beruf der Ingenieur:in (m/w/d) und vieler anderer ist daher zunehmend mathematisch geprägt.
Mathematische Methoden sind häufig Voraussetzung für den Erfolg technischer Entwicklungen; das gilt auch, wenn sie beim Endprodukt im Inneren wirken und oberflächlich nicht sichtbar sind. Deshalb nutzen Sie bereits im Studium vielfältige und umfangreiche mathematische Methoden, und hierzu legt Ihre Mathematikausbildung im Grundstudium das notwendige Fundament.
„Ich will Mathematik anwenden, wozu brauche ich Theorie?“
Theorie und Anwendung sind keine Gegensätze, sie ergänzen sich und arbeiten wunderbar effizient zusammen wie linke und rechte Hand.
Es ist in der HM völlig unmöglich, alle in späteren Anwendungen relevanten Techniken zu behandeln, sozusagen als Enzyklopädie auf Vorrat. Dazu sind die Anforderungsprofile allzu unterschiedlich: Was für den einen schon zuviel wäre, ist für die andere noch längst nicht umfassend genug. Zukünftige Ingenieur:innen sollen daher nicht nur die allgegenwärtigen Grundfertigkeiten erlernen, sondern auch mathematische Denkweisen und systematische Problemlösung, um je nach Bedarf erforderliche neue Methoden selbstständig erwerben, vertiefen und anwenden zu können.
Es ist in hochqualifizierten Berufen unwahrscheinlich, dass Sie genau dieses oder jenes Beispiel wörtlich anwenden. Das gilt ganz allgemein, selbst für die bestmögliche Auswahl von Beispielen. Hingegen ist es wahrscheinlich, dass Sie diese oder ähnliche bewährte Methoden häufig nutzen. Sie sollen daher nicht nur Beispiele lernen, sondern zugleich möglichst vielseitige Methoden!
Mathematik ist immer beides: sowohl abstrakte Theorie als auch konkrete Anwendung; sie sind keine Gegensätze, sie ergänzen sich, die eine kann nur mit der anderen dauerhaft erfolgreich sein.
„Wir haben doch Computer! Wozu lernen wir noch Mathematik?“
Sie wollen Computer korrekt und effizient nutzen? Dazu brauchen Sie Mathematik!
Mathematische Modelle und Methoden erlernen wir zunächst unter vereinfachten Laborbedingungen, in kleinem Maßstab, sozusagen unter dem Mikroskop. Unter Industriebedingungen ist ihre Vielfalt oft nur mit Computerhilfe voll auszuschöpfen. Umso wichtiger ist es, die Zusammenhänge und Mechanismen grundlegend zu verstehen:
Algorithmen und Programme implementieren mathematische Modelle!
Meist können wir nicht in ein laufendes Programm eingreifen, um ad hoc mit unserer „Intuition“ oder „Anschauung“ oder „gesundem Menschenverstand“ zu korrigieren, was die „dumme Maschine“ alleine nicht richtig macht. (Solche Formulierungen zeigen, dass wir die Situation nicht verstanden haben!) Im Gegenteil müssen wir vorhersehen, wie ein Verfahren im Detail funktioniert, um korrekte Anweisungen zu formulieren. Hierzu müssen wir sorgfältig arbeiten, akribisch jeden möglichen Fall berücksichtigen.
Je nach verlangtem Sicherheitsniveau reicht manchmal schon eine Skizze auf der Rückseite eines Briefumschlags, meist jedoch liefert nur eine genaue Analyse die nötige Sicherheit. Die Mathematik stellt hierzu alles Nötige zur Verfügung.
Dem Anwenden muss das Erkennen vorausgehen.
Max Planck (1858–1947)
„Wie bestehe ich die Klausur?“
Eine faire Klausur bedeutet: Ihr Erfolg ist proportional zu Ihrem Können.
Die Klausur ist daher keine Lotterie: Ihr Können ist proportional zu Ihrer Übung.
Pokern Sie nicht auf eine knappe Vier, das geht meistens schief. Seien Sie mutig und arbeiten Sie auf eine Zwei oder Drei, dann läuft's. Doppelter Vorteil: Die mathematischen Grundlagen, die Sie hier lernen, nützen Ihnen auch sonst überall! Jetzt schon und ein Leben lang.
Wenn Sie durchfallen wollen, dann ignorieren Sie all meine Ratschläge. Dann müssen Sie nächstes Jahr wieder ran oder Ihr Studium beenden. Manche finden Kamikaze scheinbar toll, ich kann davon nur abraten. Wenn Sie wissen wollen, wie es richtig geht, dann erinnern Sie sich an Ihre guten Erfahrungen aus der HM1&2 und lesen Sie hier die weisen Ratschläge zur HM3. Wenn Sie unsicher sind, besprechen Sie sich mit älteren erfahrenen Kommilitonen oder fragen Sie vertrauensvoll Ihr HM3-Team.
Wir sorgen dafür, dass Sie in dieser Veranstaltung alles Nötige lernen und trainieren können. Nutzen Sie dies und erfüllen Sie Ihren Teil! Verdienen Sie sich eine gute Note!
„Wie absolviere ich die HM3 erfolgreich?“
Anspruchsvolle Themen – die Mathematik ist ein typisches Beispiel unter vielen – lernen Sie nicht durch bloßes Zuschauen. Sie müssen selbst aktiv werden:
- Nutzen Sie die Vorlesung, arbeiten Sie engagiert mit, stellen Sie Fragen: vor allem sich selbst, dann anderen, gerne auch den TutorInnen, AssistentInnen, DozentInnen.
- Nutzen Sie jede Gelegenheit zum Üben, bereiten Sie sich möglichst gut auf die Gruppenübungen vor, machen Sie Ihre Hausaufgaben so selbstständig wie möglich.
- Reservieren Sie jede Woche ausreichend Zeit für Ihre eigene Arbeit. Mathematik ist derzeit nicht Ihr Lieblingsfach? Dann planen Sie noch etwas mehr Zeit ein!
Zeit ist kostbar, Sie sollten sie effizient einsetzen. Vielleicht müssen Sie Kompromisse machen, etwa hinsichtlich anderer Veranstaltungen. In jedem Fall sollten Sie wissen: 9LP bedeutet 270 Arbeitsstunden, und die werden Sie für die HM3 wirklich brauchen.
Manche werden meinen Rat missachten und das Gegenteil versuchen; damit machen sie es sich unnötig schwer. Ich sehe das mit Sorge, kann sie aber nicht davon abhalten.
Sie haben an dieser Universität große Freiheiten und damit auch eigene Verantwortung. Werden Sie dieser Verantwortung gerecht, planen und handeln Sie weise, investieren Sie Woche für Woche die nötige Lernzeit in die Mathematik.
„Was bringt mir die Teilnahme an der Vorlesung?“
Vor allem: Information, Motivation, Interaktion.
Die mündliche Präsentation der Techniken und Anwendungen wird von den meisten Teilnehmer:innen gewünscht und von vielen erfolgreich genutzt: Sie bietet eine gut fokussierte Auswahl, eine lebendige Darstellung und zudem die Interaktion zwischen Lehrenden und Lernenden. Das sollten Sie nicht unterschätzen: Viele aktive Teilnehmer:innen betonen im Rückblick die hilfreiche Ansprache, Motivierung, Interaktion und Erklärung durch die Vorlesung.
Das geht selbstverständlich über die bloß physische Anwesenheit hinaus: effizientes und erfolgreiches Lernen erfordert Neugier, Offenheit, Aufmerksamkeit, Engagement.
Vorlesungen sind eine sehr spezielle Form der Kommunikation, wie jede Form der Lehre nützen sie vor allem denjenigen, die lernen wollen. Der Besuch einer Vorlesung bringt rein gar nichts für Verirrte, die sich nur berieseln / beschallen / unterhalten lassen wollen, die hauptsächlich Licht / Wärme / WLan suchen, oder nebenbei Computerspiele / Videos / Musik konsumieren. Wenn Sie das für maßlose Übertreibungen eines realitätsfernen Professors halten, dann machen Sie einmal den schmerzhaften Reality Check und beobachten eine große Vorlesung aus der letzten Reihe! Das sollte bedenken, wer leichtfertig behauptet, diese oder jene Vorlesung sei unverständlich. Unverständlich für wen? bei welcher Art von Teilnahme?
Das Studium erfordert Engagement, Disziplin und Konzentration. Ihre Investition wird reich belohnt durch viel Aha und Freude am Verstehen.
„Was lernen Student:innen an der Uni, wenn sie nicht hingehen?“
Erfahrungsgemäß: zu wenig zu spät.
Zeit Campus schrieb hierzu am 18.12.2015: „Es ist eine erbitterte Diskussion: Die Studierenden reagieren auf Anwesenheitspflicht allergisch, die Dozenten erachten das Studium ohne Anwesenheit als sinnlos.“ Diese Diskussion tobt auch in der Mathematik.
Nach Aussagen aktiver Teilnehmer:innen bietet der mündliche Vortrag eine lebendige Erklärung und erleichtert den Einstieg ins eigenständige Üben und Lernen. Dennoch geht die Mehrheit der Student:innen nicht zur Vorlesung, wie man jedes Semester leicht nachzählen kann. Das ist bedauerlich, aber aller Erfahrung nach nicht zu ändern. Gerne wird der Verdacht geäußert, das läge am Dozenten: eine wunderbar bequeme Ausrede, ein unverhohlen pauschaler Vorwurf und Hohn für alle wirklich engagiert Lehrenden. Seien Sie ehrlich, stellen Sie sich den Herausforderungen Ihres Studiums: Entwickeln Sie das nötige Engagement, die Disziplin und die Konzentration! Das kann man lernen.
Daher mein Rat: Gehen Sie in die Vorlesung und arbeiten Sie engagiert mit!
Doch vorerst dieses halbe Jahr
Nehmt ja der besten Ordnung wahr.
Fünf Stunden habt Ihr jeden Tag;
Seid drinnen mit dem Glockenschlag!
Johann Wolfgang von Goethe (1749–1832),
Faust
„Genügt es, einfach das Skript zu lesen?“
Theoretisch ja, erfahrungsgemäß nein.
Sie benötigen das Training der wöchentlichen Übungen und vermutlich auch die direkte Ansprache der Vorlesungen. Als zusätzliches Angebot sind meine Vorlesungsunterlagen auch eigenständig nutzbar. Das hatten sich viele Hörer ausdrücklich gewünscht, zum Nacharbeiten, zur Klausurvorbereitung, oder auch als Ersatz zur Vorlesung.
Kostenlose Verfügbarkeit ist ein Geschenk; mühelose Lernbarkeit ist eine Illusion.
Wenn Sie vollkommen autark arbeiten wollen, können Sie das Skript auch selbstständig durcharbeiten; einige Teilnehmer:innen haben tatsächlich die nötige Motivation, Disziplin und Vorbereitung, und sind damit erfolgreich. Wenn Sie Anleitung brauchen oder sich unsicher sind, kommen Sie einfach zur Vorlesung, das kostet wenig und bietet viel.
Sind Online-Angebote wie Skripte, Videos, Turorials etc. die Kur oder das Übel?
Hierzu sagt John Hennessy, Präsident der Stanford University, im Interview mit der Zeit vom 22.03.2016: "Eines ist klar: Die Revolution fällt aus. Das Präsenzstudium bleibt der Normalfall. Wir Menschen brauchen fürs Lernen die persönliche Ansprache, das Mentoring, die Unterstützung." Die fehlende Präsenz und Interaktion während der Corona-Semester bestätigen dies schmerzhaft.
„Wie ist die Mathematik strukturiert?“
Die Mathematik ist extrem klar strukturiert, das erleichtert das Lernen:
- Haben Sie keine Angst vor neuen Begriffen: Definitionen erklären, Beispiele illustrieren und Sätze bündeln die Rechenregeln.
- Ein gut verstandenes Beispiel nützt Ihnen mehr als ein schlecht verstandener Satz. Nutzen Sie ernsthaft die zahlreichen Aufgaben zur eigenen Übung!
- Erarbeiten Sie sich parallel dazu die nötigen Grundlagen und verfestigen Sie Ihr Wissen in Form von Definitionen und Sätzen.
- Ein gut verstandener Satz bündelt 1000 Beispiele.
Diese explizite und extrem klare Struktur ist eine Besonderheit der Mathematik: Definition, Beispiel, Satz, Beweis, Anwendung, ... Diese typisch mathematische Sprech-, Schreib- und Sichtweise ist für Studierende anfangs ungewohnt, sie scheint zunächst skurril, vielleicht sogar abschreckend. Sie hat sich aus guten Gründen entwickelt und durchgesetzt: Sie strukturiert die Darstellung und betont das Wesentliche. Sie wird überall genutzt, weil sie sich bewährt. Es gibt keinen Grund, sie zu fürchten, im Gegenteil: Nutzen Sie sie als Hilfestellung!
„Wie lerne ich erfolgreich Mathematik?“
Kurze Antwort: Durch neugieriges Aufnehmen und eigenes Anwenden.
Mancher lernt gut aus Büchern, ein anderer besser aus Vorlesungen, ein dritter beginnt mit den Übungen, ein vierter mit den Klausuren. Alle schauen gerne YouTube-Videos, das gibt einen ersten Einblick, ist unterhaltsam und vielleicht auch hilfreich. Ihre individuellen Lernstrategien und Motivationen kennen Sie selbst am besten und sollten sie optimieren.
Das bloße Lesen / Hören / Zuschauen ist leider wenig ergiebig, denn dieser Eindruck bleibt oberflächlich und verflüchtigt sich schnell. Entscheidend ist in jedem Fall, dass Sie selbst aktiv werden, mit Stift und Papier, und schrittweise lernen, Probleme eigenständig zu lösen.
Es ist und bleibt eine menschliche Grundtatsache: Wir leben und streben, lernen und entwickeln uns, indem wir uns Erfahrungen, Wissen und Können aktiv aneignen.
- Bilden Sie Lerngruppen, diskutieren Sie die Aufgaben.
- Schreiben Sie nicht ab, sondern versuchen Sie alles selbst.
- Bleiben Sie neugierig, präzisieren und klären Sie Ihre Fragen.
Besonders gut bewährt sich die Kombination aus kontinuierlicher eigener Vorbereitung und gemeinsamer Diskussion in der Gruppe. Genau darauf zielen unsere wöchentlichen Übungen. Vertrödeln Sie während des Semester nicht diese entscheidende Gelegenheit.
Es gibt nichts Gutes,
außer man tut es.
Erich Kästner (1899–1974)
Die Kunst des Scheiterns: meine miesgelaunte Meckerecke
An dieser Stelle kotze ich mich aus, wenn ich es nicht mehr aus- oder einhalten kann, etwa nach einem weiteren aufopfernden, aber für manche erfolglosen Versuch, Höhere Mathematik zu unterrichten. Ich sollte das nicht schreiben, und Sie sollten es nicht lesen. Warum tun wir es dennoch? Ich weiß es nicht.
Warning! The following content may be inappropriate for some audiences. By clicking here you confirm that you understand the risk and wish to continue reading.
Sind die vielbeschworenen Vortragsübungen Teil der Lösung oder Teil des Problems?
Manche Teilnehmer:innen verlangen vehement weitere Lehrangebote, traditionell Vortragsübungen und Videoaufzeichnungen. Mich erstaunt dabei immer wieder ein gemeinsames Muster: Existierende Angebote werden ignoriert — „Ich pfeife auf Vorlesungen und Übungen!“ — gleichzeitig aber immer neue Angebote gefordert — „Ich brauche Vortragsübungen und Videoaufzeichnungen!“ Mir scheint das eine Flucht vor unbequemen Wahrheiten zu sein. Selbst zu arbeiten ist mühsam, Forderungen zu erheben ist bequem.
„Bei Vortragsübungen sehe ich, wie man Übungen löst und bekomme alle Tricks erklärt.“ Ja, sicher, das Wichtigste ist, dass Sie selbst aktiv werden! Die Vorlesung zeigt Ihnen hierzu alle nötigen Werkzeuge, übrigens auch an Beispielen und Anwendungen. Sie sind doch schon in einem höheren Semester, warum haben Sie Vortragsübungen überhaupt noch nötig? Warum schauen Sie lieber jemandem beim Rechnen zu, als es selbst einmal zu versuchen? Sicher, kleinschrittige Vorführungen sind anfangs hilfreich, in den ersten Semestern bietet die HM1&2 genau dies: Sie werden an die Hand genommen und behutsam geführt. Wann sind Sie bereit für erste eigene Schritte?
„Ich brauche Anleitung.“ Sicher, am Anfang brauchen Sie kleinschrittige Anleitung und leuchtende Vorbilder. Babies füttert man geduldig mit Brei, doch Kleinkinder gewöhnt man nach und nach an feste Nahrung. Kindern liest man liebevoll Geschichten vor, doch nach und nach sollen sie selbst lesen lernen. In Ihrem Studium sollen Sie die kindliche Unmündigkeit überwinden und zu erwachsener Selbstständigkeit reifen. Die Vorlesung erklärt Ihnen alles Nötige und in den Übungen können Sie es anwenden. Wie bitte? Achso, zur Vorlesung gehen Sie nicht, und die Übungsaufgaben schreiben Sie nur ab. Seufz. Ja, gut, so gesehen geben Vortragsübungen wenigstens das behagliche Gefühl, irgendwie dabei zu sein.
Das Ausflüchtekarussel: „Ich kann erst anfangen zu arbeiten und zu lernen, wenn...“
Manche Teilnehme:innenr machen ernsthafte und sinnvolle Verbesserungsvorschläge, andere erheben lieber Forderungen. „Die Vorlesung kann ich unmöglich verstehen. Bevor ich es versuche, verlange ich ... ein Buch! ... noch mehr Bücher! ... nein, besser ein Skript! ... ein ganz ausführliches Skript! ... Ohje, das Skript scheint viel zu lang, ich will ein Kurzskript! ... Ich benötige ... mehr Übungen! ... mit Lösungen! ... mit ganz ausführlichen Lösungen! ... Nein, besser Vortragsübungen, da muss ich nicht selbst rechnen, sondern kann beim Rechnen zuschauen. ... Auch das kostet Mühe, daher fordere ich pauschal mehr Anwendungsbezug... Ach nein, reale Anwendungen sind lang und kompliziert. ... Das ist mir doch zu lästig. Ich fordere ... Videos! ... ausführliche Erklärvideos! ... auf mich maßgeschneidert ... kurz und doch ausführlich! ... mit Musik! ... und Tanz! ... Die Vorlesung muss unbedingt als Musical aufgeführt werden ... nein, besser als Rockoper ... mit aktuellen Hits ... Die Klausur naht und ich bin immer noch verwirrt. Ich will ... alte Klausuren! ... mehr alte Klausuren! ... mit ausführlichen Lösungen! ... Die alten Klausren verstehe ich leider nicht. Ich brauche... hm... eine Vorlesung! Ach, hätte ich doch jetzt bloß eine Vorlesung!“ Das Ausflüchtekarussel dreht sich jedes Jahr munter im Kreis. Ich fürchte, es wird auch diesmal wieder so kommen.
Ich höre den Argumenten der Studierenden seit Jahren geduldig und aufmerksam zu und versuche, die Spreu vom Weizen zu trennen. Viele Verbesserungen konnten so identifiziert und umgesetzt werden. Das ist nicht leicht und kostet viel Mühe, doch es dient einem guten Zweck: Die Vorlesung und die Übungen und alle Angebote drumherum sind daran gereift. Inzwischen ist das Potential zur Optimierung weitgehend ausgeschöpft. Natürlich kann ich immer noch mehr anbieten, aber der Nutzen muss die Kosten rechtfertigen. Ich kann die oben karikierten Ausflüchte zwar verstehen, doch gutheißen kann ich sie nicht. Für Ihren Erfolg in Studium und Beruf gilt das obige Motto: Es gibt nichts Gutes, außer man tut es.
Bitte machen Sie sich nichts vor: Es mangelt nicht an unserem Angebot an Sie oder an unserer Unterstützung für Sie. Der limitierende Faktor ist Ihr eigenes Engagement. Krempeln Sie die Ärmel hoch und engagieren Sie sich in Ihrem Studium!
Der Giftschrank: todsichere Anti-Tipps – Bitte nicht lesen... und nicht nachmachen!
Ich erkläre jedes Jahr deutlich und eindringlich, worauf es ankommt. Die einen werden sich redlich bemühen und erfolgreich sein. Die anderen werden die Mühe scheuen und scheitern. Ich vereinfache etwas, aber weniger als Sie vielleicht glauben... Entscheiden Sie weise, planen Sie realistisch, wählen Sie nicht den vermeintlich leichten Weg, sondern den richtigen Weg. Sorgen Sie dafür, dass Sie Ihr Ziel erreichen und Ihr mathematisches Werkzeug beherrschen!
Wenn Sie scheitern wollen, dann geht es ganz sicher so:
-
Sie haben im Studium keinerlei Pflichten: „Ich lasse mich nicht zwingen!“
Variante: „Die Dozent:in muss die Studierenden da abholen, wo sie sind.“ -
Gehen Sie nicht zur Vorlesung: „Das sind mittelalterliche Lehrmethoden.“
Variante: Gehen Sie mal hin, aber hören Sie nicht zu. „Miese Lehre.“ -
Ignorieren Sie Übungen und Hausaufgaben: „Das ist bloß autoritäre Gängelei.“
Variante: Schreiben Sie sinnlos ab. „Ich verschwende keine Zeit mit Nachdenken.“ -
Lesen Sie niemals Bücher, nicht einmal ein Skript: „Unnütze Theorie.“
Variante: Blättern Sie planlos darin herum. „Alles völlig unverständlich.“ -
Versuchen Sie nicht mitzudenken oder selbstständig zu arbeiten: „Uninteressant.“
Variante: Kritisieren Sie pauschal die „Theorielast“, fordern Sie „Praxisbezug“. -
Bereiten Sie sich nicht auf Klausuren vor, oder nur oberflächlich: „Reine Lotterie“.
Variante: Käuen Sie alte Klausuren ohne Verständnis. „Reine Schikane.“ -
Verachten Sie redliche Arbeit, vertrauen Sie auf Wunder: „Weniger ist mehr.“
Variante: „Nächste Woche / Monat / Jahr / Studium lege ich richtig los.“ -
Suchen Sie die Schuld nicht bei sich: „Die Dozent:in hat utopische Ansprüche.“
Variante: Reden Sie alles schön. „Ich habe eigentlich alles gewusst.“ -
Misstrauen Sie der Erfahrung und allen guten Ratschlägen Ihrer Lehrenden:
„Im Studium sagt einem eh niemand, worauf es wirklich ankommt.“ -
Absorbieren und verbreiten Sie wirre Verschwörungstheorien:
Wenn man schon in die Irre geht, dann wenigstens nicht alleine.
Sie finden diese Liste absurd? Ich stimme zu, Sie sprechen mir aus der Seele.
Sie finden diese Ansichten überzeugend? Bitte suchen Sie professionelle Hilfe!
Ever tried. Ever failed. No matter.
Try again. Fail again. Fail better.
— Wieder versuchen. Wieder scheitern. Besser scheitern.
Samuel Beckett (1906–1989), Worstward Ho
Fragen und Antworten zu den Gruppenübungen
Erkläre es mir, und ich werde es vergessen.
Zeige es mir, und ich werde mich erinnern.
Lass es mich tun, und ich werde es verstehen.
Konfuzius (551–497 v.Chr.)
Ihr HM3-Team stellt Ihnen jede Woche gut abgestimmte Aufgaben, damit Sie die Techniken der Höheren Mathematik einüben, verfestigen und vertiefen. Unser gemeinsames Ziel ist, dass Sie Ihre mathematischen Werkzeuge klausurfest beherrschen. Laut Modulbeschreibung: selbstständig, sicher, kritisch, korrekt und kreativ. Vorlesung, Übung, Klausur sind eng aufeinander abgestimmt: Die Vorlesung erklärt Ihnen die Begriffe und Techniken, in der Übung trainieren Sie ihre korrekte und sichere Anwendung, in der Klausur stellen Sie schließlich Ihr Können unter Beweis. Die Übungen haben dabei die zentrale Scharnierfunktion, Ihr kontinuierliches persönliches Engagement ist der Schlüssel zu Ihrem Erfolg! Zu diesem einfachen Grundprinzip erkläre ich hier einige Folgerungen.
Es gibt drei Möglichkeiten, klug zu handeln:
1. Durch Nachahmen — Das ist die leichteste.
2. Durch Nachdenken — Das ist die edelste.
3. Durch Erfahrung — Das ist die bitterste.
Konfuzius (551–497 v.Chr.)
„Wozu dienen die Übungen?“
Ihre wöchentlichen Übungsgruppen dienen Ihrem Trainung und Ihrer Vorbereitung; sie sind unser wichtigstes Angebot an alle Teilnehmer:innen, um die neuen Werkzeuge einzuüben und selbstständig anzuwenden. Das kostet Geduld und Mühe, aber es lohnt sich!
Bitte bearbeiten Sie ernsthaft alle Übungsaufgaben, nur so lernen Sie das Handwerk.
Wenn Sie spezielle Fragen haben, die in der Übung nicht berücksichtigt werden können, dann wenden Sie sich bitte direkt an Ihr HM3-Team, also an Ihre Tutor:innen, Assistent:innen oder Dozent:innen. Im Ilias-Kurs betreuen wir hierzu ein Forum.
„Warum ist das jede Woche nötig?“
Die behandelten Techniken werden im weiteren Fortgang der aktuellen Vorlesung benötigt und verwendet, zudem sind sie Grundlage für alle Anwendungen der folgenden Semester.
Warten Sie mit Ihrer notwendigen Eigenarbeit nicht bis zum Ende des Semesters: Schwierige Projekte werden leichter, wenn Sie sie kleinschrittig angehen. Wer das Gegenteil behauptet, dem ist wohl kaum zu helfen.
Investieren Sie jede Woche die nötigen 6-8 Stunden eigene Arbeitszeit! Das strukturiert Ihre Arbeit und Sie bleiben im Takt. Der Erfolg Ihrer Übungen beruht auf Ihrem persönlichen Engagement.
„Wie verlaufen die Gruppenübungen?“
Die Höhere Mathematik ist, wie Sie bereits aus der HM1&2 wissen, extrem effizient organisiert und führt Sie auf eine steile Lernkurve. Das gilt auch für die HM3: Die Vorlesung präsentiert alle Themen ausführlich im Wechselspiel der zugrundeliegenden Theorie (alle nötigen Begriffe und Techniken, Definitionen und Sätze) und konkreten Anwendungsbeispielen (Aufgaben mit Lösungen): Beide Sichtweisen ergänzen sich und helfen gegenseitig zur Erklärung. Nutzen Sie beides, wie linke und rechte Hand.
In den Gruppenübungen bearbeiten Sie anschließend weitere Aufgaben eigenständig, um Ihre mathematische Techniken einzuüben und Ihre Problemlösungsfähigkeiten zu trainieren. Das ist das Ziel, Ihr Engagement in den Übungen ist daher der entscheidende Punkt! All unsere Aufgaben erfüllen den studentischen Wunsch nach regelmäßiger Übung, von einfachen Übungen bis zu klausurtypischen Aufgaben. Das ist anstrengend, aber lohnend!
Auf Wunsch der Studierenden führen wir das Übungssystem der HM1&2 fort: Die Übungsblätter enthalten zwei Arten von Aufgaben: Die Präsenzaufgaben lösen Sie gemeinsam in den Übungsgruppen, dabei werden Sie soweit nötig von unseren TutorInnen unterstützt. Die darauf aufbauenden Hausübungen erarbeiten Sie eigenständig und geben sie ihrer Tutorin oder ihrem Tutor ab. Diese/r korrigiert Ihre Abgabe und gibt Ihnen individuelle Rückmeldung zum aktuellen Lernstand, Hinweise zur Bearbeitung, Tipps und Tricks, etc. Erfahrungsgemäß lernt man es nur, wenn man es selbst versucht, ernsthaft, dauerhaft.
„Lohnt sich der große Aufwand für die Übungen?“
Sie werden merken: Gut vorbereitet sind die Präsenzübungen für alle profitabel, die Hausübungen leichter zugänglich, und die investierte Zeit zahlt sich aus. Besser Sie arbeiten kontinuierlich und erfolgreich jede Woche als zu spät und erfolglos im Hauruck. Sie werden sehen: Ihre Ergebnisse rechtfertigen diese gemeinsame Anstrengung.
Sie fühlen sich durch diese Vorschriften gegängelt und bevormundet? Seien Sie versichert, es geschieht zu einem guten Zweck: Wer ernsthaft Fußball spielen will, muss zum Training erscheinen und dort auch trainieren. Wer ein Instrument spielen will, muss regelmäßig üben. Wer Ingenieur:in werden will, muss sein Handwerkszeug lernen und parat haben.
Es gibt klare Vorteile: Lernen müssen Sie Ihr Handwerkszeug so oder so, also am besten rechtzeitig und gleich richtig, gemeinsam und gut betreut während des gesamten Semesters. Die kontinuierliche Investition während des Semesters wird Ihnen vielleicht sogar Freude bereiten, da Sie jede Woche neue Techniken erwerben und Probleme lösen können, die zuvor noch außerhalb Ihrer Reichweite lagen. Wir nehmen es sportlich und versuchen das beste.
Training ist regelmäßige Belastung zum Zwecke der Leistungssteigerung.
Es bezeichnet im Sport einen komplexen Handlungsprozess
– meist unter Anleitung und Kontrolle von Trainern –
zur Verbesserung des sportlichen Leistungszustands und
zur bestmöglichen Leistungspräsentation in Bewährungssituationen.
Wikipedia zum Stichwort „Training“
„Ich kann/will meine Aufgaben nicht selbst lösen. Genügt es, sie abzuschreiben?“
Nein. Wenn Sie sich diese Frage ernsthaft stellen, dann kann ich Ihnen nicht helfen. Vermutlich auch sonst niemand. Nur Sie selbst können sich Ihr Handwerk aneignen, Wissen und Können, Grundlagen und Training. Bitte tun Sie's!
„Für die Übungen benötige ich jede Woche mehrere Stunden. Ist das nicht zu lang?“
Nochmal: Ihr Lernerfolg braucht Zeit und Ruhe, vor allem aber Ihr Engagement! Arbeiten Sie gründlich, oberflächliche Schnellbleiche hilft Ihnen nicht. Ihr Handwerk können Sie nicht im Vorübergehen erlernen. Ein Hochschulstudium ist nunmal schwierig und erfordert Ihr ernsthaftes Bemühen und intensive Arbeit, das kostet Zeit, das ist unvermeidlich. Nehmen Sie die Herausforderung an!
Genau hierzu sind Ihre Vorlesung und Ihre Aufgaben (Präsenz- und Hausübungen) und Ihre Klausuren (Schein- und Abschlussprüfungen) aufeinander abgestimmt. Wenn Sie zur Lösung die nötigen Grundlagen noch erlernen müssen, dann sollten Sie hierzu Ihre individuelle Lernzeit angemessen einplanen. Das ist eine gute Investition: Sie brauchen Grundlagen und Training. Wenn Sie auf diese Weise Ihr Handwerk erlernen: Gut so!
Und ja, mehrere Stunden Arbeit pro Woche sind vollkommen normal.
„Wieviele Stunden benötige ich jede Woche für die HM3?“
Die Antwort ist schockierend einfach und jedesmal wieder einfach schockierend:
Für die HM3 benötigen Sie etwa 270 Stunden, das entspricht 15 Wochen zu je 14 Stunden pro Woche plus etwa 60 Stunden Prüfungsvorbereitung! Das bedeutet jede Woche 7 Stunden Vorlesung+Übung und etwa 6-8 Stunden eigene Arbeit. Es gilt die Erhaltung der Arbeit: Wenn Sie Vorlesung+Übung schwänzen, dann bleiben etwa 14 Stunden eigene Arbeit pro Woche.
Ich sage es nochmal auf bolonesisch-technokratisch: Für diese Veranstaltung sind 270 Arbeitsstunden veranschlagt (= 9 Leistungspunkte mal 30h/LP). Davon verbringen Sie etwa 105 Stunden in Vorlesung und Übung (= 15 Semesterwochen mal 7h/Woche, wobei ich je 45min zu 1h aufrunde). Es bleiben etwa 165 Stunden eigene Arbeit. Das entspricht weiteren 7 Stunden in jeder der 15 Semesterwochen plus 60 Stunden Prüfungsvorbereitung in der vorlesungsfreien Zeit vor der Klausur. All diese Stunden werden Sie als wertvolle Lern- und Übungszeit wirklich brauchen! Insbesondere sollten Sie sich schon zu Beginn die Proportionen klar machen: Das Hauruck-Verfahren kurz vor der Prüfung ist ziemlich aussichtslos, es wird oft planlos versucht, doch es funktioniert einfach nicht. Sie werden nur dann guten Erfolg haben, wenn Sie kontinuierlich arbeiten.
„Lernen kostet Zeit und bereitet Mühe! Lohnt sich diese Investition?“
Die Faktenlage ist klar, wer sie ignoriert scheitert aller Wahrscheinlichkeit nach.
Wer es hingegen ernsthaft versucht, dem gelingt die HM3 erfahrungsgemäß gut.
„Das kann doch nicht so schwer sein. Wo liegt das Problem?“
Alle Beteiligten wissen: Neues lernt man nur durch ausgiebiges Üben, das gilt ganz besonders für mathematische Methoden und Rechentechniken. Sie müssen sich also entscheiden zwischen dem leichten Weg und dem richtigen Weg. Leider investieren oft diejenigen am wenigsten Zeit und Mühe, die am meisten Einarbeitung und Übung benötigen: Diese häufig beobachtete Fluchtreaktion ist zunächst verständlich, aber dennoch vollkommen verkehrt: Recipe for failure!
Weder verständlich noch tolerierbar sind die Auswüchse: Vorlesungen werden mit Computerspielen abgesessen, Eigenarbeit als überflüssig belächelt, ja geradezu verachtet, Hausaufgaben ignoriert oder notfalls abgeschrieben, Gruppenübungen nicht vorbereitet, Übungszeit vergeudet oder gleich geschwänzt. Kurz vor der Prüfung verbreitet sich saisonale Panik oder Fatalismus, aber nach der Prüfung ist selbst das schnell vergessen. Routinemäßg angeprangert werden jedoch nicht die Ursachen, sondern die Symptome: die viel zu schweren Themen und die zu hohe Durchfallquote, die verständnislosen Dozent:innen und ihre utopischen Forderungen.
Seien Sie ehrlich, stellen Sie sich den Herausforderungen Ihres Studiums: Entwickeln Sie das nötige Engagement, die Disziplin und die Konzentration! Das können Sie lernen, das müssen Sie lernen.
„Ist die Schein- oder Abschlussklausur vorhersehbar?“
Ja. Gefragt wird, was zuvor in der Vorlesung erklärt und den Übungen trainiert wurde.
Zudem ist die Klausur fair gestellt: Ihr Erfolg ist proportional zu Ihrem Können.
Die Klausur ist keine Lotterie: Ihr Können ist proportional zu Ihrer Übung.
Aus dieser verlässlichen Prognose lesen Sie sofort die optimale Lernstrategie ab: Nutzen Sie die Vorlesung, arbeiten Sie engagiert mit, machen Sie die Übungen, trainieren Sie regelmäßig jede Woche. Das ist arbeitsintensiv, und es lohnt sich.
Jetzt denkt sich manche/r: „Ich bin clever und vergeude keine Zeit mit Lernen.“ Nein! Das ist nicht clever und auch keine Ersparnis, im Gegenteil: So vergeuden Sie Ihr Studium, bestenfalls korrigieren Sie Ihre Strategie nach einigen vertanen Semestern, schlimmstenfalls scheitern Sie endgültig und stehen am Ende ohne Abschluss da. Die Warnung ist ernst, die vermeintliche Abkürzung ist ein Sackgasse.
„Genügt es als Abkürzung, alte Klausuren zu rechnen?“
Der gut rhythmisierte Ablauf Vorlesung - Übung - Scheinklausuren - Klausur hat sich in vielen Jahrzehnten bewährt. Viele Studierende machen es umgekehrt, Ihrer Abneigung oder Zeitnot gehorchend, und beginnen mit den Klausuren: Das kann jedoch nur funktionieren, wenn sie sich gleichzeitig die nötigen Grundlagen erarbeiten. Das gelingt nicht in ein paar Tagen, etwa als Panikaktion vor der Klausur: Recipe for Desaster!
Sie brauchen Ruhe und Zeit zum Arbeiten und Lernen.
Alle Vorgehensweisen brauchen Zeit, und zwar gleich viel!
Für die HM3 im Umfang von 9LP benötigen Sie etwa 270 Arbeitsstunden.
Es gilt die Erhaltung der Arbeit, es gibt keine magische Abkürzung.
Wer das Gegenteil behauptet ist ein Scharlatan oder fällt demnächst durch.
Nochmal zur Betonung: Ich empfehle ausdrücklich das Üben anhand von alten Klausuren. Dies ist eine sehr gute Ergänzung, aber kein Ersatz zu Vorlesung und Gruppenübung. Die Aufgaben variieren von Klausur zu Klausur, mit wohlüberlegter Absicht, damit möglichst alle Themen und Techniken vertreten sind. Stumpfes Auswendiglernen von Beispielen genügt nicht, investieren Sie Ihre Lernzeit ausgewogen in Methoden und Beispiele, das ist wesentlich effizienter!
Why waste time learning,
when ignorance is instantaneous?
Hobbes (1985–1995)
„Sind die Aufgaben in der (Schein-)Klausur auch so schwer wie in den Übungen?“
Kurze Antwort: Jein. Die Aufgaben der (Schein-)Klausur sind kurz und leicht, dafür müssen Ihnen alle Rechnungen zügig und fehlerfrei von der Hand gehen. Das ist, wie Sie wissen, eine eigene Disziplin und benötigt Training, Sicherheit und Routine. Genau diese Übung erwerben Sie in den 15 Wochen des Semesters.
Unsere Übungsaufgaben folgen eng der Vorlesung und decken soweit möglich alle Themen ab. Sie sind daher eher umfangreich und dienen als umfassendes Training, zu Wiederholung und Einübung; dafür benötigen Sie jede Woche etwa 6-8 Stunden.
In der Klausur begegnen Ihnen dieselben Aufgabentypen; anders als bei Ihrer wöchentlichen Arbeit (etwa 15×8h = 120 Stunden) ist die Klausurzeit mit 120 Minuten sehr kurz, für jede Aufgabe stehen nur etwa 20 Minuten zur Verfügung. Die Aufgaben sind daher enger gesteckt und vom Umfang auf die Prüfungssituation zugeschnitten. Der wichtigste Faktor für Ihren Erfolg ist daher: Sie müssen Ihr Handwerkszeug flüssig beherrschen und geübt haben. Verständnis und Rechenfertigkeit erwerben Sie durch die Bearbeitung von Vorlesung und Übung. Das ist Ihr Ziel.
„Die Übungsausgaben sind schwer und lang. Muss das sein?“
Kurz gesagt: Ja. No pain, no gain. Es ist gut und wichtig, dass Sie die Übungsaufgaben ernst nehmen und damit Ihr Handwerk trainieren. Ja, sie können schwer und lang sein, insbesondere wenn Ihnen die richtigen Methoden fehlen. Die sollen Sie ja gerade erlernen und erproben! Die gute Nachricht: Mit den Techniken der Vorlesung lassen sich die Aufgaben leichter und schneller lösen. Genau diese Techniken sollen sie verstehen und einüben! Nehmen Sie daher die Vorlesung ebenso ernst; beide sind aufeinander abgestimmt. Stochern Sie nicht hilflos im selbstverbreiteten Nebel. Definitionen und Sätze helfen Ihnen, Aufgaben effizient und korrekt zu lösen.
„Gibt es Lösungen zu den Übungsaufgaben?“
Ja, nach dem Abgabetermin finden Sie unsere Lösungen online. Das war ein ausdrücklicher Wunsch der Teilnehmer:innen und entlastet die Gruppenübungen.
„Können wir Ihnen auch außerhalb der Sprechstunden Fragen stellen?“
Ja, gerne, einige Teilnehmer:innen nutzen das bereits und schauen bei Gelegenheit vorbei. Die Sprechzeiten sind nicht exklusiv gemeint, sondern als Zusage und Ermutigung und zur Vereinfachung, wann Sie uns auf jeden Fall gut erreichen können.
„Warum halten Sie Vorlesung und Vortragsübung gemeinsam?“
Genau genommen bekommen Sie wöchentlich drei Vortragsübungen mit integrierter Vorlesung. In der Vorlesung präsentiere ich die wenigen Definitionen und zentralen Sätze und erkläre hierzu sofort zahlreiche Aufgaben und Anwendungsbeispiele. Das war ausdrücklicher Wunsch der Studierenden: Übung, Übung, Übung! Um die nötige Zeit zu gewinnen, reduziere ich die grundlegende Theorie auf das zum Verständnis notwendige Minimum, ich spare an Beweisen auch wenn's wehtut, zudem integriere ich die Vorlesung und die Vortragsübung. Dieses Konzept scheint sehr gut aufzugehen.
„Bei klassischen Vortragsübungen kann ich mehr vorbereiten und selbst üben.“
Ja, gut möglich. Erfahrungsgemäß hat das die letzten Jahre leider nicht funktioniert, da die Zeitbelastung im dritten Semester guten Vorsätzen wenig Entfaltung bietet. (Das ist nur ein Teil der Wahrheit und eine höfliche Beschönigung: Wie Sie wissen hat mancher einfach keine Lust oder frönt gar der Faulheit.) Aber es stimmt natürlich: Es ist nützlich und effizient, wenn Sie sich die Aufgaben vor dem Vortrag anschauen. Alle Aufgaben liegen schriftlich vor, Sie können sich damit also gut vorbereiten. Da Sie jedoch mit anderen Vorlesungen mehr als ausgelastet sind, vermutlich auch mit den Gruppenübungen der HM3 (siehe oben), ist ein eventuelles Nacharbeiten wohl realistischer.
„Warum eilen wir mit drei Terminen pro Woche durch den Stoff der HM3?“
Der übliche Rhythmus sind fünf Termine in je zwei Wochen, verteilt auf 15 Semesterwochen, also insgesamt 37 oder 38 Termine. Ich nutze diesmal sechs Termine in je zwei Wochen, verteilt auf 13 Wochen, also insgesamt ebenfalls 37 oder 38 Termine. Der Unterschied ist nicht gewaltig, aber doch spürbar: Wir haben zwölf Wochen lang je eine Stunde mehr (20%). Wir sind dadurch bereits Mitte Januar mit der Vorlesung fertig, alle Themen können also noch in Ruhe durch die Übungen laufen, und wir entgehen Ende Januar dem alljährlichen Abgabefieber für diverse andere Projekte. Außerdem haben wir jede Woche einen einheitlichen Rhythmus. Ich hoffe, diese Vorteile überwiegen.
Wer sät, muss mähen. // Und wer mäht, muss säen.
Nichts bleibt, mein Herz. Und alles ist von Dauer.
Erich Kästner (1899–1974)
Literatur
Schauen Sie sich in der Bibliothek Lehrwerke zur Höheren Mathematik an und wählen Sie das für Sie passende aus. Wenn Sie möchten, können Sie mit folgenden anfangen:
- K. Meyberg, P. Vachenauer: Höhere Mathematik, Band 1 und 2
- G. Bärwolff: Höhere Mathematik für Naturwissenschaftler und Ingenieure.
-
K. Burg, H. Haf, F. Wille, A. Meister: Höhere Mathematik für Ingenieure,
Dank Campuslizenz der Uni Stuttgart als EBook, Band 1, 2, 3, 4, 5, 6 - R. Ansorge, H.J. Oberle: Mathematik für Ingenieure, Band 1 und 2
- E. Kreyszig: Advanced Engineering Mathematics
- W. Kimmerle: Mehrdimensionale Analysis und Differentialgleichungen
Zur Wiederholung der mathematischen Grundlagen:
Wiederholung, Training, Vorbereitung:
- Klausurenarchiv der HM3 (vertieft): Scheinklausuren und Abschlussklausuren
- Klausurenarchiv der Höheren Mathematik in Stuttgart: Abschlussklausuren
- Mathematik Online (Skripte, Übungsaufgaben, Tests)
Zur Vertiefung der Grundlagen und einzelner Themen:
- H. Heuser (KIT Karlsruhe): Lehrbuch der Analysis (1-2)
- H. Heuser: Gewöhnliche Differentialgleichungen
- S.D. Chatterji (EPFL Lausanne): Cours d'analyse (volume 1-3)
- I.N. Bronstein, K.A. Semendjajew: Taschenbuch der Mathematik
- M. Abramowitz, I. Stegun: Handbook of Mathematical Functions (pdf)
- G. Doetsch: Laplace Transformation (Das EBook scheint mit unserer Campuslizenz leider nicht zugänglich, aber immerhin die L-Tabelle im Anhang.)
Chuck Norris liest keine Bücher:
Er starrt sie so lange an, bis sie ihm
freiwillig sagen, was er wissen will.
Wiederholung, Training, Vorbereitung
Well, what kind of world do we live in
When eleven and seven equals two?
John Mellencamp (1951–), J.M.'s Question
Nochmal zur Betonung: Ihr HM3-Team stellt Ihnen jede Woche gut abgestimmte Aufgaben, damit Sie die Techniken der Höheren Mathematik einüben und vertiefen. Unser gemeinsames Ziel ist, dass Sie diese klausurfest beherrschen. Laut Modulbeschreibung: selbstständig, sicher, kritisch, korrekt und kreativ.
Einige Teilnehmer:innen haben mich um weitere Aufgaben zum Einüben gebeten.
Die einen wollen möglichst leichte Fingerübungen zum Einstieg, die anderen wollen möglichst realistische Anwendungen, die sind anderen wiederum zu kompliziert, einige wollen klausurtypische Aufgaben, die sind anderen noch zu schwer, usw. Hier müssen Sie sich etwas umschauen und nach Ihren Bedürfnissen auswählen. Vielleicht konsultieren Sie zunächst Ihr Lieblingslehrbuch in der Bibliothek (siehe oben).
Dennoch will ich Ihrem Wunsch gemäß hier anfangen, ein paar Aufgaben zu sammeln.
- Alle Beispiele und Aufgaben aus der Vorlesung; meist leicht und illustrativ.
- Alle Aufgaben aus unseren Quizzen und Gruppenübungen; darunter sind leichte und schwere, und insgesamt zeichnen sie die wichtigsten Techniken der Vorlesung nach.
- Klausurenarchiv der HM3 (vertieft): Scheinklausuren und Abschlussklausuren
Folgende Aufgaben aus Mathematik Online (eine kleine Auswahl):
- Mehrdimensionale Integration: 219, 285, 507, 849, 850, 863, 1424, 1640
- Kurvenintegral und Potential: 176, 191, 410, 420, 446, 1335
- Integralsätze von Gauss, Green, Stokes: 255, 414, 423, 472, 483, 534, 562
- Residuenkalkül: 436, 438, 806, 808, 463, 474, 543, 547
- Fourier-Reihen: 178, 185, 265, 496, 544, 662, 1354, 1444
- Fourier-Transformationen: 758, 259, 541, 1171
- Laplace-Transformation: 253, 266, 479
- Gewöhnliche Differentialgleichungen: 245, 291, 326, 536, 575, 1053, 1059, 1628, 52, 291, 529, 556, 1443, 681, 378, 181
- Differentialgleichungssysteme: 31, 83, 282, 302, 386, 531, 558, 908, 1435
- Wahrscheinlichkeitsrechnung: 1438, 1442, 1441, 1449, 1448, 1440, 1599
Klausurvorbereitung zur HM3 aus dem Begleitmaterial zu Mathematik Online (WiSe 2010/11). Wiederholung einiger Formeln, Aufgaben und Lösungen zu folgenden Themen: mehrdimensionale Integration und Integralsätze, Funktionentheorie, Fourier-Reihen, Fourier- und Laplace-Transformation, gewöhnliche Differentialgleichungen, Differentialgleichungssysteme, partielle Differentialgleichungen, Wahrscheinlichkeitsrechnung.
Now if six turned out to be nine
Oh I don't mind, I don't mind.
Jimi Hendrix (1942–1970), If 6 was 9
Abschlussklausur
Um zur Klausur zugelassen zu werden, müssen Sie als Vorleistung während des Semesters den Übungsschein erwerben oder sich einen vorigen Schein anerkennen lassen. Die Klausuren finden turnusgemäß in den Prüfungszeiträumen statt, üblicherweise Ende Februar und Anfang September. Termine und Räume werden vom Prüfungsamt zentral organisiert und bekannt gegeben, bitte informieren Sie sich dort.
Das Runde muss ins Eckige,
und die Klausur dauert 120 Minuten.
Inhalt sind alle Themen der HM3.
Erlaubte Hilfsmittel: 10 Seiten DIN A4 eigenhandgeschriebene Notizen. Stifte (schwarz oder blau, kein Bleistift oder Rotstift) und genügend leeres Papier für Ihre eventuellen Nebenrechnungen sind von Ihnen selbst mitzubringen.
(Erläuterung: Eigenhandgeschrieben bedeutet von Ihnen eigenhändig handgeschrieben. Diese Einschränkung dient vor allem Ihrer eigenständigen Vorbereitung, denn die ist das Wichtigste! 10 Seiten entsprechen 5 Blättern Vorder&Rückseite, entsprechend einer Fläche von etwa 0.624 m2; es dürfen auch weniger sein. Sonstige Hilfsmittel wie Taschenrechner, Computer, Telefone, Funkgeräte, Dronen, wissensrelevante Hirnimplantate und andere futuristische Gadgets etc. sind nicht zugelassen.)
Klausuren vergangener Jahrgänge finden Sie im Klausurenarchiv der HM3 (vertieft) (Scheinklausuren und Abschlussklausuren) sowie im gemeinsamen Klausurenarchiv der Höheren Mathematik in Stuttgart (nur Abschlussklausuren).
Wahrscheinlichkeitsrechnung ist ganz einfach.
Die Klausur bestehe ich mit 40% Wahrscheinlichkeit,
bei drei Prüfungsversuchen also mit 120%iger Sicherheit.
Fragen & Antworten zur Prüfungsvorbereitung
„Was würden Sie als optimale Prüfungsvorbereitung empfehlen?“
Als Grundlage empfehle ich Vorlesung und Lehrbücher, zum Training die Übungen und Klausuren. Manche schauen zudem gerne YouTube-Videos, das ist unterhaltsam und vielleicht auch hilfreich. Das bloße Lesen / Hören / Zuschauen ist leider wenig ergiebig, denn dieser Eindruck bleibt oberflächlich und verflüchtigt sich schnell. Entscheidend ist in jedem Fall, dass Sie selbst aktiv werden und schrittweise lernen, Probleme eigenständig zu lösen.
Theorie und Praxis sind keine Gegensätze, sondern gegenseitige Erklärung und Ergänzung: Theorie ohne Praxis ist leer; Praxis ohne Theorie ist blind.
Viele Studierende machen es umgekehrt, Ihrer Abneigung oder Zeitnot gehorchend, und beginnen mit den Klausuren: Auch das kann funktionieren – allerdings nur, wenn sie sich gleichzeitig die nötigen Grundlagen erarbeiten. Das gelingt nicht in ein paar Tagen, etwa als Panikaktion vor der Klausur: Recipe for Desaster!
Sie brauchen Ruhe und Zeit zum Lernen.
Alle Vorgehensweisen brauchen Zeit, und zwar gleich viel!
Für die HM3 im Umfang von 9LP benötigen Sie etwa 270 Arbeitsstunden.
Es gilt die Erhaltung der Arbeit, es gibt keine magische Abkürzung.
Wer das Gegenteil behauptet ist ein Scharlatan oder fällt demnächst durch.
Manchen wird diese ehrliche Antwort nicht gefallen, da sie viel Arbeit erfordert, aber gefragt ist die optimale Vorbereitung. Sie erfordert insbesondere kontinuierliche Arbeit, Woche für Woche während des gesamten Semesters. Wenn Sie vorhaben, erst wenige Tage vor der Klausur anzufangen, dann reicht es nur zum Notprogramm mit den üblichen Risiken. Vertrauen Sie statt auf Lücke lieber auf Lernen!
„Muss ich Tabellen abschreiben? Was muss in die Formelsammlung?“
Manche Klausuraufgaben nutzen Tabellen, typischerweise Funktionswerte (z.B. Exponentialfunktion, Normalverteilung) oder Integraltafeln (etwa zur Laplace- oder Fourier-Transformation). In diesem Fall sind die nötigen Tabellen dem Klausurtext beigefügt, wie etwa bei den Klausuren der Vorjahre. Die Techniken müssen Sie natürlich beherrschen: Einzelne Ergebnisse und Formeln sollten Sie vorbereiten und verstehen, und zur Klausur entweder auswendig beherrschen oder in Ihren Notizen griffbereit haben. Beispielsweise kennen Sie die Integrationsregeln der HM2 wie Substitution und partielle Integration auswendig, die Integralsätze von Gauss/Green/Stokes aus der HM3 hingegen möchten Sie lieber notieren. (Das alles hilft natürlich nur, wenn Sie diese auch verstehen und anwenden können; ohne Verständnis nützen Formeln nichts.)
„Die älteren Klausuren sind vom Stil her sehr unterschiedlich.“
Die Vorlesung HM3 für LRT und MaWi gibt es schon lange, und die Klausuren sind im Klausurenarchiv gut sortiert. Die Klausurtexte sehen vom Layout/Stil immer etwas anders aus, ich habe mich zum Beispiel für die Heftform entschieden. Thematisch aber sind die Klausuren der letzten Jahre ziemlich deckungsgleich: Integralrechnung für Funktionen mehrerer Veränderlicher, gewöhnliche und partielle Differentialgleichungen, Fourier-Reihen und Fourier-Integrale sowie Stochastik. (Über die Jahre haben die Änderungen in der Modulbeschreibung die Akzente nur unwesentlich verschoben.) Natürlich stellen wir in jeder Klausur neue Aufgaben, die Kontinuität erkennt, wer die Inhalte versteht und nicht am Buchstaben der Klausur klebt. Jedenfalls sollten Sie mit den Werkzeugen Ihrer aktuellen Vorlesung auch die alten Aufgaben lösen und als Training verwenden können.
„Kommen partielle Differentialgleichungen in der Klausur dran?“
Gewöhnliche Differentialgleichungen (ODE) und partielle Differentialgleichungen (PDE) sind ein Höhepunkt der HM3. Sie nehmen beim jetzigen Rhythmus eine zentrale Rolle in Vorlesung und Übungen ein, und entsprechend sind sie auch in der Klausur repräsentiert. Zu PDE kann die Vorlesung zwar nur einen ersten kleinen Einblick geben, doch gerade hier kommen alle Techniken wunderbar zusammen. Daher können auch PDE in der Klausur vorkommen — natürlich wohldosiert: Charakteristik-Methode oder Produktansatz führen PDE auf gewöhnliche DGSysteme zurück und eignen sich gut zu Klausuraufgaben.
„Sind die Aufgaben vom letztem Jahr noch aktuell für die diesjährige Prüfung?“
Die Höhere Mathematik ist das universelle Handwerkszeug jeder Ingenieur:in (m/w/d). Die Themen sind sorgsam vorgegeben, sie sind nicht willkürlich ausgewählt, sondern destilliert aus der langen Erfahrung Ihrer Studiengänge. Die sicherere Beherrschung quantitativer Modelle ist die Grundlage Ihres Erfolges in Studium und Beruf. Die Übungen der letzten Jahre geben diese Themen gut wieder, ebenso wie die zahlreichen Aufgaben aus Mathematik Online und dem Klausurenarchiv. An den Themen ändert sich daher kaum etwas, wir passen lediglich die Akzentsetzung an und illustrieren die Themen mit neuen Aufgaben.
Ich investiere sehr viel Zeit in ausführliche Beispiele und vielseitige Rechentechniken. Die Vorlesung verfolgt das Ziel, die Sätze möglichst gebrauchsfertig zu präsentieren. Wir stimmen die Übungen möglichst eng darauf ab. Die Übungsaufgaben geben daher ein recht getreues Abbild vom Verlauf der Vorlesung und sollen zum Training dienen. Wenn Sie die Vorlesung im Vorjahr gehört haben, können und sollten Sie auch die diesjährigen Übungen zu Ihrer Vorbereitung nutzen; das meiste werden Sie wiedererkennen.
„Gibt es im Sommersemester die Möglichkeit, den HM3-Schein zu machen?“
Für die Grundausbildung der Ingenieur:innen in Höherer Mathematik stellen die stuttgarter Ingenieurstudiengänge nur sehr knappe Ressourcen zur Verfügung. Zusatzangebote wie Prüfungsvorbereitungskurse nach dem Wintersemester oder Wiederholbarkeit von Übungen und Scheinklausur im Sommersemester scheinen mir unter Umständen sinnvoll, sind aber bei der gegenwärtigen Unterfinanzierung der Mathematik schlicht nicht möglich. Konkret heißt das: Im Sommersemester ist das HM3-Team mit anderen Veranstaltungen ausgebucht.
Es geht ja nicht nur darum, noch eine weitere Scheinklausur anzubieten, das Problem ist im Gegenteil ganz grundsätzlich: Wer es im Wintersemester mit perfekter Betreuung durch Vorlesungen und Vortragsübungen, mit Präsenzübungen und Hausaufgaben, und schließlich zwei Scheinklausuren nicht geschafft hat, der hat vermutlich ganz grundlegende Schwierigkeiten. Da genügt es nicht, weitere Klausuren als vermeintliche Punktelotterie zu verschleudern, sondern es muss von Grund auf gearbeitet werden. Ja, nochmal: Es gilt die Erhaltung der Arbeit!
Der Aufwand wäre daher enorm groß, und der Nutzen äußerst fraglich. In einigen wenigen Fällen kann ich mir einen Nutzen vorstellen, doch zweifle ich insgesamt an der Wirksamkeit dieser Maßnahme. Zusätzliche Möglichkeiten können auch als zusätzliche Ausflüchte missbraucht werden: Man kann jederzeit mit dem Lernen anfangen, also kann man es auch jederzeit aufschieben. Die Gesamtzahl der erreichten Studierenden bleibt vermutlich gleich, schlimmstenfalls fördern wir Absentismus und Aufschieberitis.
Hoher Aufwand für fraglichen Nutzen? Investieren wir lieber da, wo es sich lohnt! Der Fokus liegt derzeit und zukünftig auf der sehr aufwändigen und gut abgestimmten Veranstaltung im Wintersemester. Nutzen Sie dieses sehr gute Angebot!
„Wird es im vorlesungsfreien Zeitraum von Ihnen organisierte Prüfungsvorbereitungskurse geben?“
Fortsetzung der vorigen Antwort: Als Notlösung ist Last-Minute-Lernen zwar weit verbreitet, aber erfahrungsgemäß wenig effizient. Während des Wintersemesters bieten Ihnen die Vorlesung und die Übungen eine hervorragende wöchentliche Betreuung. Das sollten Sie nutzen! Prüfungsvorbereitungskurse lindern etwaige Versäumnisse, sind aber ansonsten nicht notwendig. Ich sehe Vor- und Nachteile und bin für Experimente offen.
In einigen der letzten Jahre konnten wir einen Prüfungsvorbereitungskurs als zusätzliches, freiwilliges Angebot durchführen, dank des Engagements derTutor:innen der HM3 als einwöchigen Kompaktkurs im Februar nach Ende der Vorlesung und vor der Klausur. Der Zeitraum war gut gewählt, das gemeinsame Lernen sehr produktiv, und diese Möglichkeit wurde von einer großen Zahl der Studierenden durchgängig positiv angenommen. In dieser Form war das Experiment extrem erfolgreich.
Die zukünftige Finanzierung der Tutoren muss allerdings noch gefunden werden.
In der Theorie gibt es keinen Unterschied
zwischen Theorie und Praxis.
In der Praxis schon.
Fragen & Antworten zur mündlichen Fortsetzungsprüfung
„Was bedeutet diese Nachprüfung?“
Kurze Antwort: Diese Prüfung ist Ihre letzte Chance.
Wenn Sie sich diese Frage stellen, sind Sie vermutlich in folgender Situation: Sie sind bei den Klausuren zu dieser Veranstaltung mehrfach durchgefallen und sind nun dabei, Ihren Prüfungsanspruch in Ihrem Studienfach endgültig zu verlieren. Das ist absolut ernst. Die mündliche Fortsetzungsprüfung ist Ihre letzte Chance zu beweisen, dass Sie nicht Ihre bislang wiederholt festgestellte Note Fünf verdienen, sondern mindestens eine Vier. Wer die Fortsetzungsprüfung als weiteres Freilos missbraucht, ist völlig fehlgeleitet. Nehmen Sie diese letzte Chance wirklich ernst und bereiten Sie sich so gründlich wie möglich vor.
„Was wird gefragt?“
Es handelt sich um eine mündliche Fortsetzungsprüfung, also keine eigenständige neue Prüfung. Ich frage Sie daher zu den Themen der Klausur, meist ausgehend von zwei oder drei Aufgaben, mit denen Sie Schwierigkeiten hatten, allerdings nicht dieselben Fragen, sondern Variationen des Themas. Es genügt daher nicht, die fertig vorliegende Musterlösung auswendig zu lernen und abzuspulen. Sie müssen nicht nur ein Beispiel kennen, sondern die zur Lösung notwendigen Methoden beherrschen. Da die Klausur eine breite Themenauswahl abdeckt, gilt dies auch für die mündliche Fortsetzungsprüfung.
„Muss ich Rechnungen ausführen?“
Ja, denn nur so können Sie zeigen, dass Sie Ihr Handwerk beherrschen. Am besten sorgen Sie also durch gründliche Vorbereitung dafür, dass Ihnen einfache Rechnungen auch zügig von der Hand gehen. Aus Zeitgründen können Sie in 20 Minuten natürlich nur sehr begrenzte Rechnungen vorführen. Vor längeren Rechnungen erklären Sie besser kurz, was Sie eigentlich tun und warum; Teile davon können und sollen Sie dann ausführen, das klärt sich im Dialog recht schnell. So beweisen Sie sowohl Ihr Wissen als auch Ihr Können.
„Brauche ich meine Formelsammlung?“
Nein. In der mündlichen Prüfung werden Sie Ihre Formelsammlung kaum brauchen; Sie müssen schon wissen, wie's geht. Wenn Sie einmal stocken, mir aber sagen können, wie's weitergehen sollte und welche Formel Sie dazu brauchen, dann will ich Ihnen gerne aushelfen, das ist ein entscheidender Vorteil der mündlichen Prüfung. Das ist natürlich nur eine Hilfestellung und keineswegs Ersatz für Ihre eigene Leistung. Sie wollen überzeugen. Sie müssen liefern.
„Wie soll ich mich vorbereiten?“
Als Vorbereitung empfiehlt sich der gesamte gefragte Stoff, genauso wie auch schon zur Vorbereitung der schriftlichen Prüfung. Es geht nun allerdings nur noch um die Frage, die bisherige Note Fünf zu bestätigen oder aber aufgrund Ihrer überzeugenden mündlichen Leistung auf eine Vier anzuheben. Planen Sie zu Ihrer Vorbereitung ausreichend Zeit ein!
Wenn Sie sich diese Frage vier Wochen vor Ihrer Prüfung stellen, dann können und müssen Sie diese Zeit intensiv nutzen für gründliches Lernen. Ausgehend von Ihrem bisherigen Lernstand ist das schwierig, es erfordert Disziplin und Ausdauer, aber erfahrungsgemäß ist es möglich. Wenn Sie sich diese Frage erst wenige Tage vor Ihrer Prüfung stellen, dann ist es für eine ernsthafte Vorbereitung zu spät.
„Ich will doch nur noch eine Vier, die schafft doch jeder, oder?“
Nein. Mit guter Vorbereitung geht's, ohne geht's erfahrungsgemäß nicht.
Lernen Sie also nicht auf Lücke und zielen Sie nicht auf die Note 4.499, das geht schriftlich schief und mündlich ebenso. Auch wenn es tragisch ist, erfahrungsgemäß fallen jedes Jahr auch einige Prüflinge endgültig durch. Die Anforderungen dieses Moduls gelten natürlich weiterhin, auch in einer mündlichen Fortsetzungsprüfung. Bereiten Sie sich daher so umfassend und gründlich wie möglich vor, und übertreffen Sie Ihre bisher vorliegenden schriftlichen Ergebnisse. Überzeugen Sie Ihre Prüfer:in, dass Sie die behandelten Methoden selbstständig, sicher, kritisch, korrekt und kreativ anwenden können. Das ist das erklärte Ziel dieser Lehrveranstaltung laut Modulhandbuch.
Quidquid agis, prudenter agas et respice finem!
— Was immer du tust, handele klug und bedenke das Ende!
nach Äsop
Termine und Themen
Vorhersagen sind schwierig,
besonders über die Zukunft.
Die Inhalte der gehaltenen Vorlesungen notiere ich im Laufe des Semesters hier stichpunktartig. Der Zeitplan für zukünftige Termine ist naturgemäß noch vorläufig und Änderungen unterworfen. Den genauen Inhalt der Vorlesung entnehmen Sie den Folien.
| Vorlesungsbeginn am 15. Oktober 2024 | |
| V01 Di 15.Okt | Willkommen zur HM3! Überblick und Ausblick: Ziele der Vorlesung anhand motivierender Anwendungen. Organisatorisches zum Ablauf. [bis 207] |
| V02 Di 15.Okt | §A Was sind und was sollen Integrale? A1 Volumen. A3 Integral. §B Eindim. Integration. B1 Einschachtelung, HDI. B2 Ausschöpfung. [B206] |
| V03 Fr 18.Okt | §C Mehrdimensionale Integration. C1 Satz von Fubini, absolute Integrierbarkeit. Beispiele. C2 Transformationssatz. Polarkoordinaten. [C209] |
| V04 Di 22.Okt | Gaußsche Glockenkurve mit Kunstgriff. Zylinder- und Kugelkoordinaten, Volumina. C4 Trägheitsmomente von Zylinder und Kugel. [C413] |
| V05 Di 22.Okt | C4 Warnendes Gegenbeispiel. Serviettenring. §D Grenzwerte. D1 Integral und Reihe. D2 Integral und Grenzwert. D3 Integral und Ableitung. [D418] |
| V06 Fr 25.Okt | D4 Feynman-Trick. §E Integralsätze in der Ebene: Motivation, anschauliche Beispiele, von Summen zu Integralen. E1 Satz von Green & Gauß. [E141] |
| V07 Di 29.Okt | Green & Gauß erklären, nachrechnen, anwenden. E2 Schreibweise als Differentialform, Flächenformel, Herzkurve. [E218] |
| V08 Di 29.Okt | E3 Wirbelfeld und Quellenfeld. §F Integralsätze für komplexe Funktionen. F1 Komplexe Wegintegrale, fundamentale Beispiele, Holomorphie. [F109] |
| V09 Di 05.Nov | F1 Überblick. Residuensatz, Beispiel Fourier-Integrale. F4 Residuen, Polstellen. Residuensatz und zahlreiche Anwendungen. [F430] |
| V10 Di 05.Nov | G1 Integralsätze im Raum. G2 Stückweise glatte Flächen, Torus, Guldinsche Regeln. G3 Orientierung, Rechte-Hand-Regel. Satz von Stokes. [G316] |
| V11 Fr 08.Nov | G3 Satz von Gauß. Anwendung: Archimedisches Prinzip. Numerik: Polyeder, Triangulierung. G4 Beispiele: abgestumpfte Kugel, Iglu. [G416] |
| V12 Di 12.Nov | §H Anwendungen der Integralsätze. H1 Von der Physik zum Integral zur PDE: Kontinuitätsgleichung, Wärmeleitungsgleichung. [H201] |
| V13 Di 12.Nov | H2 Vektorfelder: exakt gdw konservativ. Rotationsfrei ist notwendig, auf einfach zshgden Gebieten auch hinreichend für ein Potential. [H340] |
| V14 Fr 15.Nov | I1 Periodische Signale, Skalarprodukt und Orthonormalbasis. I2 Fourier-Analyse, Sägezahnfunktion, Konvergenz-Kriterium von Dirichlet. [I220] |
| V15 Di 19.Nov | Treppenfunktionen. I3 Differenzieren und Integrieren, Dreieckfunktion, Parabelfunktion. Glattheit und Abklingen der Fourier-Koeffizienten. [I410] |
| V16 Di 19.Nov | §J Energiegleichung (Parseval), Beispiele, Fourier-Isometrie (Fischer-Riesz), isoperimetrische Ungleichung (Hurwitz). §K Motivation [K110] |
| V17 Fr 22.Nov | §K Fourier-Transformation. K1 Motivation, Beispiele, Umkehrsatz. K2 Rechenregeln. K3 Fourier-Isometrie. K4 Anwendungsbeispiele. [K417] |
| V18 Di 26.Nov | §L Laplace-Transformation. L1 Definition, Beispiele, Regeln. L2 L-Tabelle. Lösung einer ODE als AWP. §M ODE, Beispiele aus der Mechanik. [M114] |
| V19 Di 26.Nov | M1 Separation der Variablen. Existenz, Eindeutigkeit, gut gestellt. M2 Exakte DG, Potential, Lösungen sind Niveaulinien. Integrierender Faktor. [M210] |
| V20 Fr 29.Nov | Wie finden wir integrierende Faktoren? Beispiele, lineare DG. M3 Fazit. M4 Substitution: lineare Subs., Ähnlichkeits-DG, Bernoulli-DG. [M414] |
| V21 Di 03.Dez | N1 Harmonische Schwingungen, frei und erzwungen, explizite Lösung aller Fälle, Resonanz. N2 Lösungsraum, Fundamentallösungen. [N203] |
| V22 Di 03.Dez | N2 Lineare DG mit konstanten Koeffizienten, charakteristisches Polynom und Fundamentalsystem, spezielle rechte Seite, Greensche Lösungsformel. [N303] |
| V23 Fr 06.Dez | O1 Gekoppelte Schwingungen, Entkopplung. DGSysteme erster Ordnung, Anwendungen, E&E-Satz. O3 Linearität, Struktur des Lösungsraumes. [O304] |
| V24 Di 10.Dez | Beispiele zur Entkopplung. Variation der Konstanten, Lösungsformel. P1 Reihe von \(n\) Oszillatoren, Produktansatz, stehende Wellen. [P108] |
| V25 Di 10.Dez | P1 Eigenvektoren & Eigenfunktionen, Diagonalisierbarkeit, Hauptvektoren & Hauptfunktionen, Jordan-Basen, Lösung aller lin. DGSysteme. [P147] |
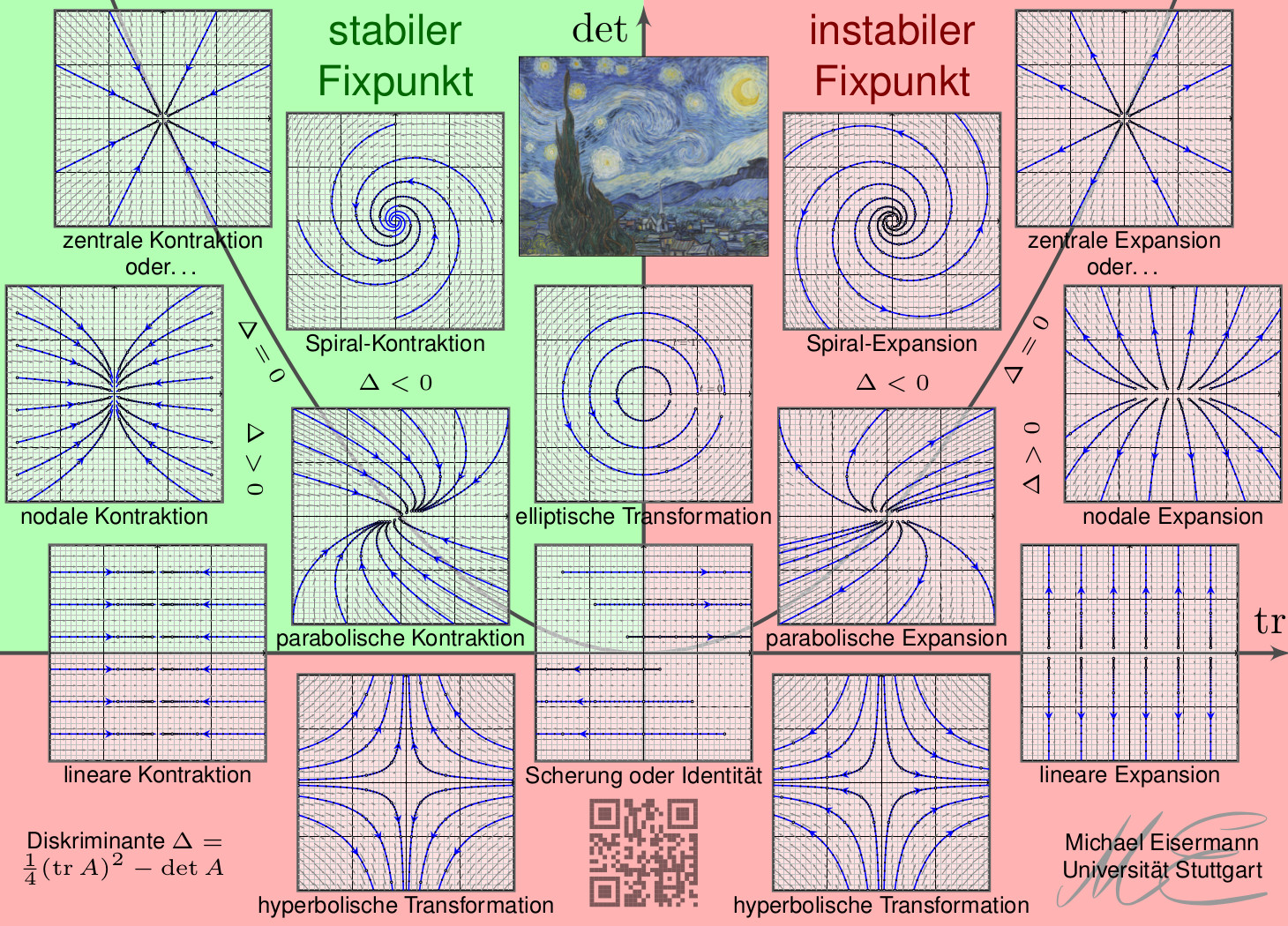
| V26 Fr 13.Dez | P2 Gleichgewichtslagen, Linearisierung, Stabilität, zweidim. Klassifikation. Anwendungsbeispiele, der torkelnde Tennisschläger. [P256] |
| V27 Di 17.Dez | §Q PDE. Q1 Wichtige Beispiele. Q2 (Quasi-)Lineare PDE erster Ordnung. Lösung entlang charakteristischer Kurven, Transportgleichung. [Q234] |
| V28 Di 17.Dez | R1 Lineare PDE zweiter Ordnung, Klassifikation. Produktansatz, ARWP, Fourier-Reihen. S1 Wärmeleitung, Fundamentallösung, freie Lösung. [S206] |
| V29 Fr 20.Dez | S2 Stab: Trennung der Variablen durch Produktansatz, ARWP mit Fourier-Reihen. S4 Kugel: Produktansatz, ARWP, Anwendungsbeispiele. [S420] |
| Weihnachtsferien vom 21. Dezember 2024 bis zum 5. Januar 2025 | |
| V30 Di 07.Jan | §T Wahrscheinlichkeitsrechnung. T1 Diskrete WRäume, Rechenregeln, Beispiele. T2 Bedingte Wkt, totale Wkt und Bayes, Anwendungen. [T216] |
| V31 Di 07.Jan | Unabhängigkeit. T3 Zufallsvariablen, Erwartung, Varianz, Chebychev. Fubini: Erwartung eines Produkts, Varianz einer Summe, Gegen/Beispiele. [T333] |
| V32 Fr 10.Jan | GGZ nach Chebychev. Wiederholte Messungen: Sicherheit vs Genauigkeit vs Kosten. Korrelation vs Kausalität. T4 Sex, Kicker, Irrfahrt. [T452] |
| V33 Di 14.Jan | §U Kombinatorik & Näherungen. U1 Ausfall, Kollision. U2 Urnenmodelle. U3 Hypergeometrische, Binomial-, Poissonverteilung. [U322] |
| V34 Di 14.Jan | Totaler Abstand, Fehlerschranken. Warenprüfung. V1 Kontinuierliche WVerteilungen. V2 Kenngrößen. V3 Der lokale Grenzwertsatz (LGS). [V313] |
| V35 Fr 17.Jan | Anwendungen, Fehlerschranken, Korrekturterm. W1 Summen unabhängiger ZV. Der zentrale Grenzwertsatz (ZGS). W2 Konfidenzintervalle. [W202] |
| V36 Di 21.Jan | Stichprobenschätzung: Alice und Bob spielen um echtes Geld. [45min] Konfidenzintervall (Neyman). Meinungsforschung. Venus Express. [W228] |
| V37 Di 21.Jan | W4 Entropie in Mathematik, Physik und technischer Thermodynamik. Schlusswort: Gehet hin in Frieden, suchet Weisheit und findet Erleuchtung. |
| Vorlesungsende am 8. Februar 2025 | |
| Feb | Abschlussklausur / Modulprüfung. |
| Apr | Klausurergebnisse und Termin zur Einsicht |
| Mai | Spacenight 2025. Handele klug und bedenke das Ende: Tun Sie schon im Wintersemester alles dafür, dass Sie im Mai allen Grund zum Feiern haben! |
Vienne la nuit sonne l'heure
Les jours s'en vont je demeure
Passent les jours et passent les semaines
Ni temps passé ni les amours reviennent
Appolinaire (1880–1918), Le Pont Mirabeau
![[banner]](/igt/eiserm/banners20/Lascaux-1.jpg) Michael Eisermann
Michael Eisermann