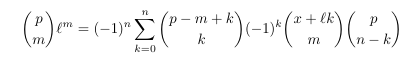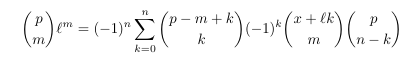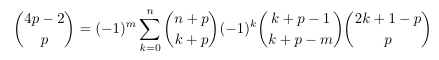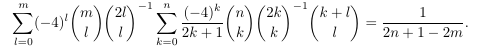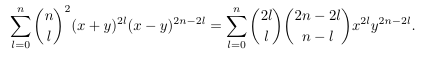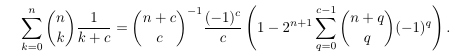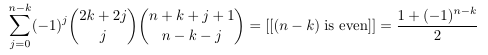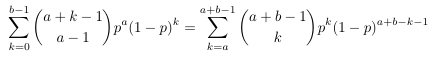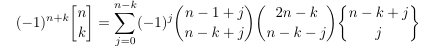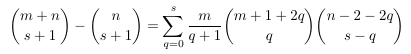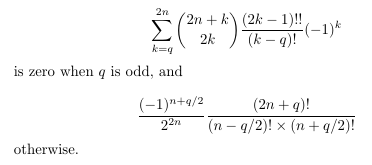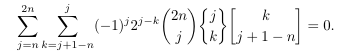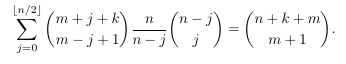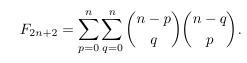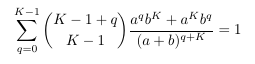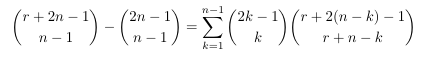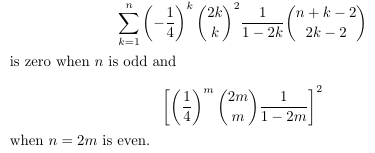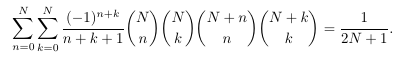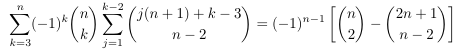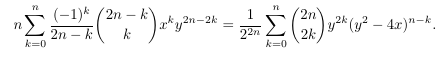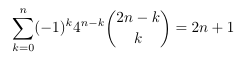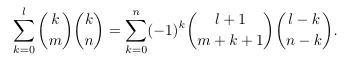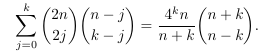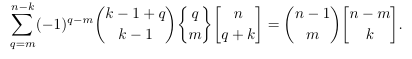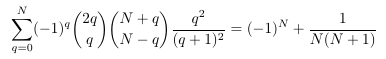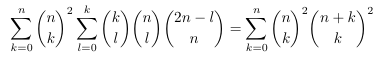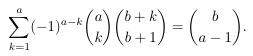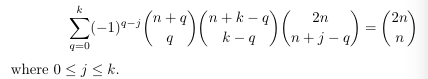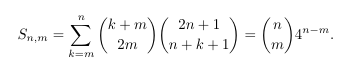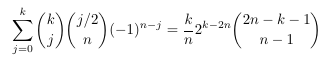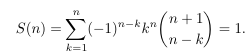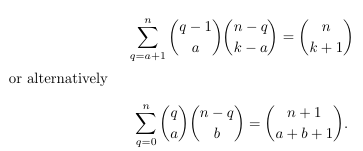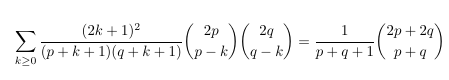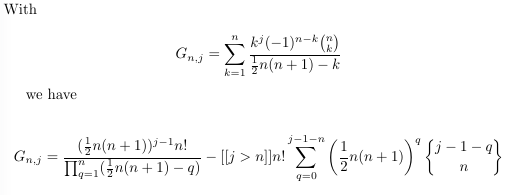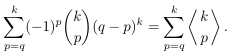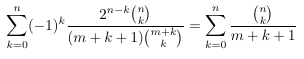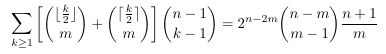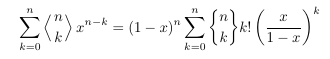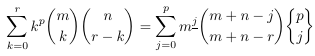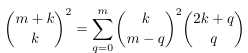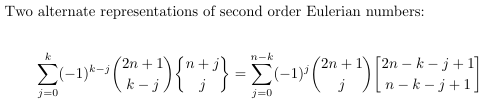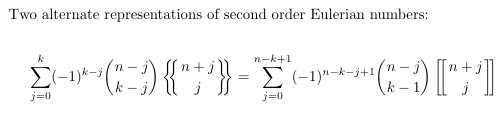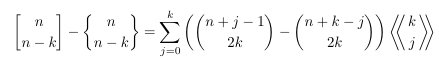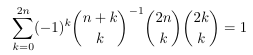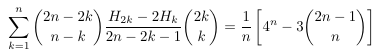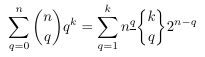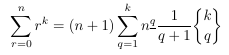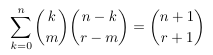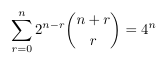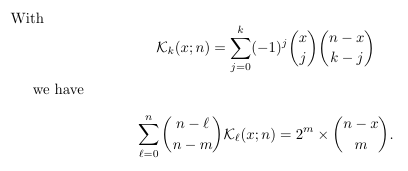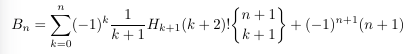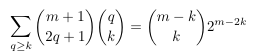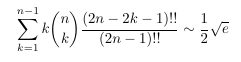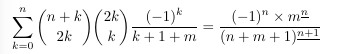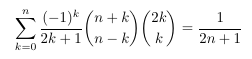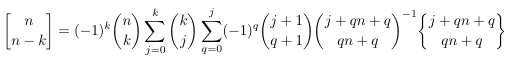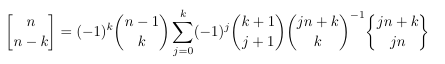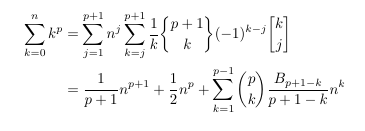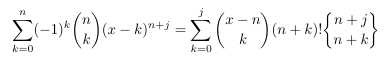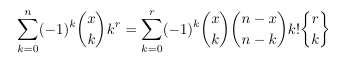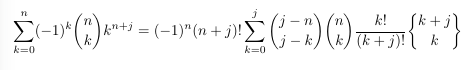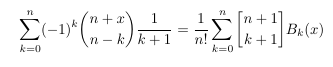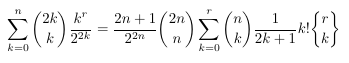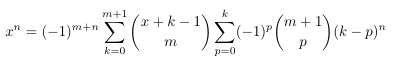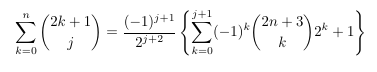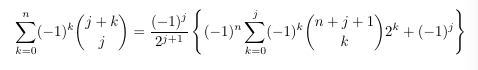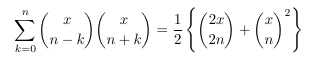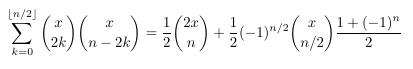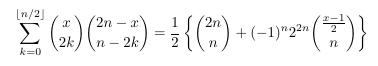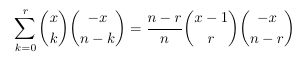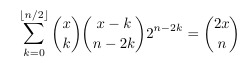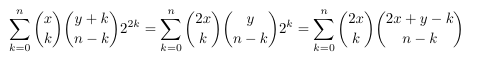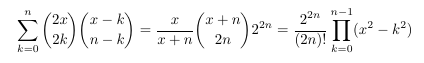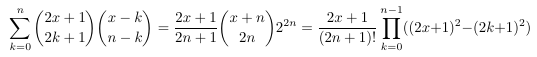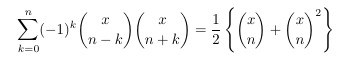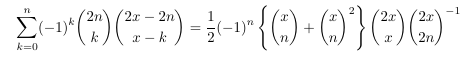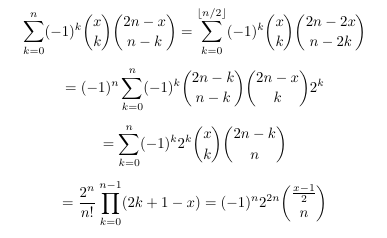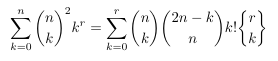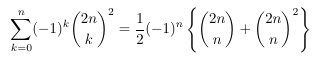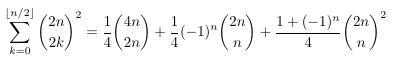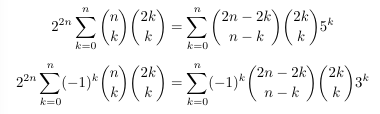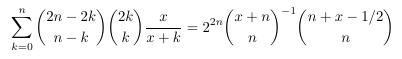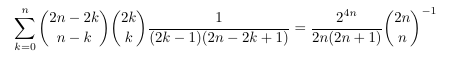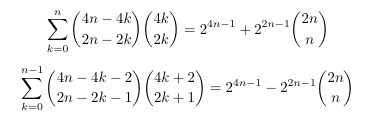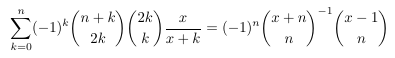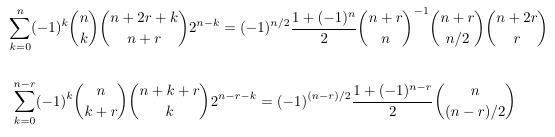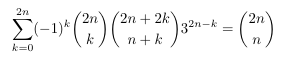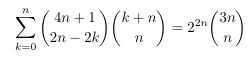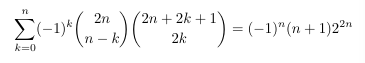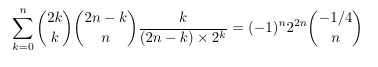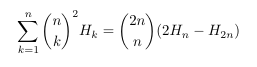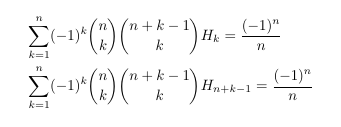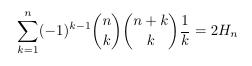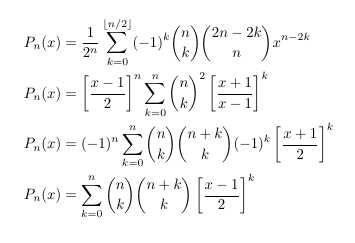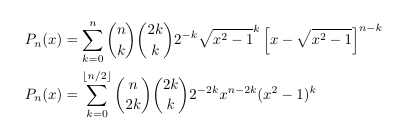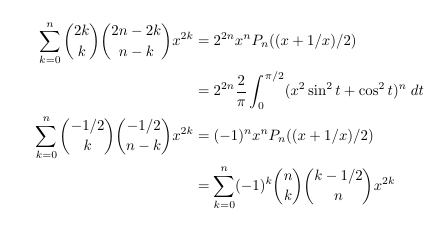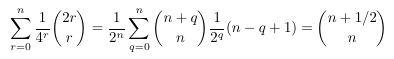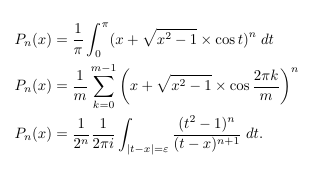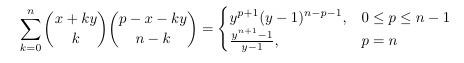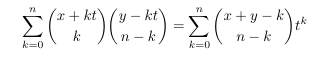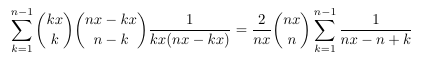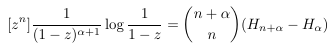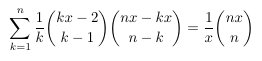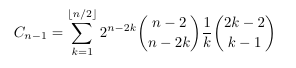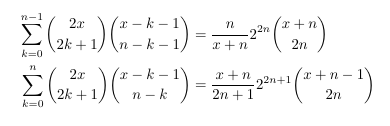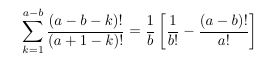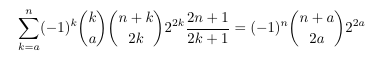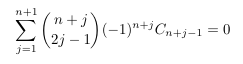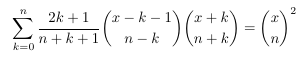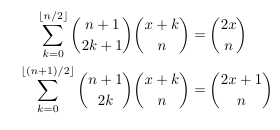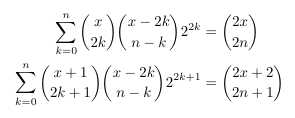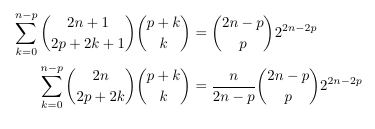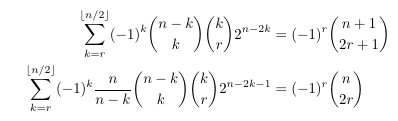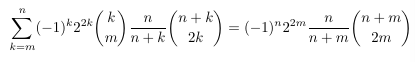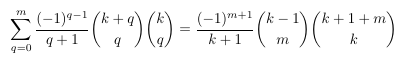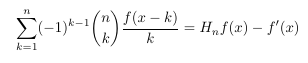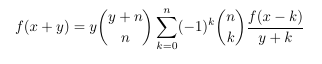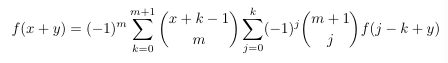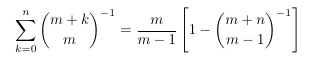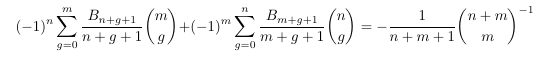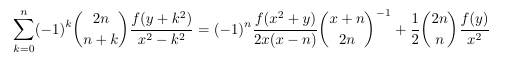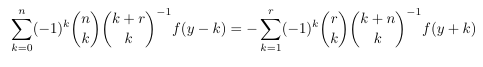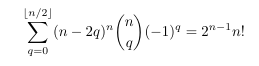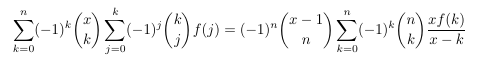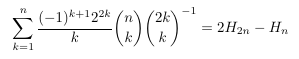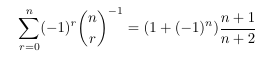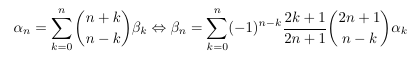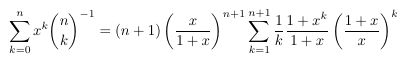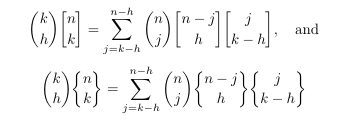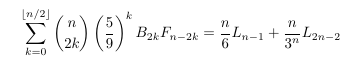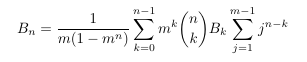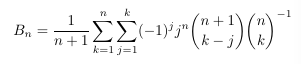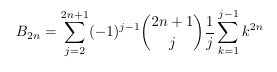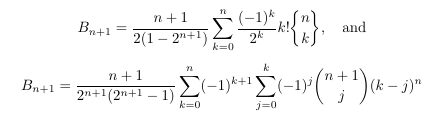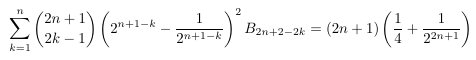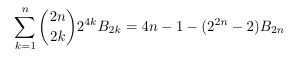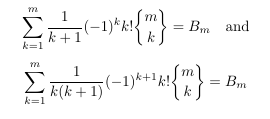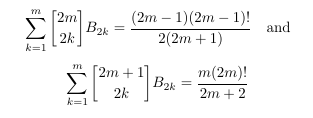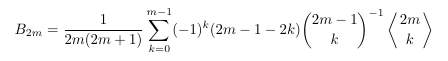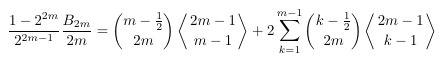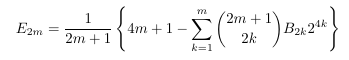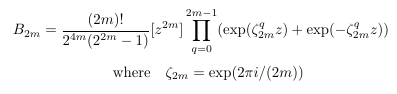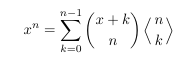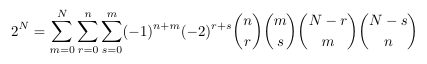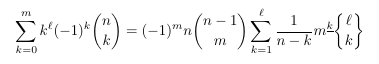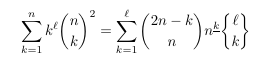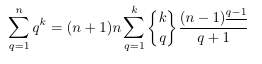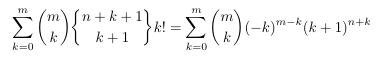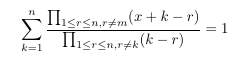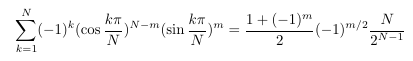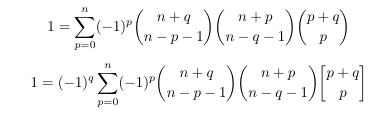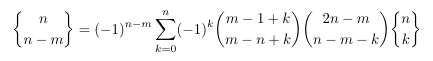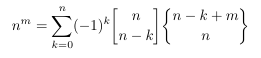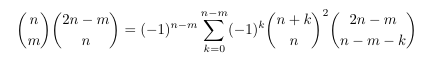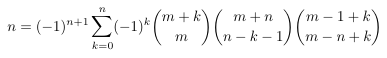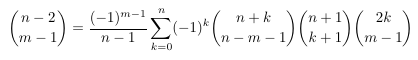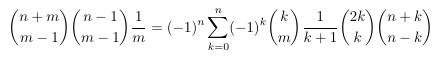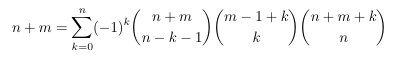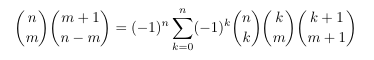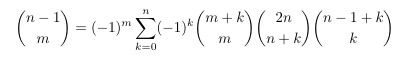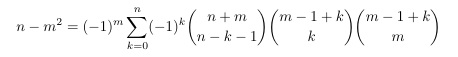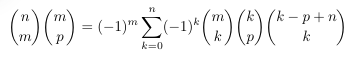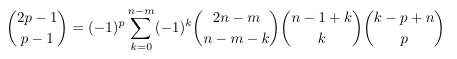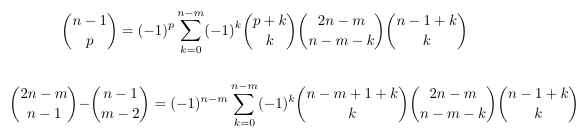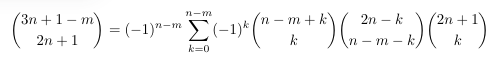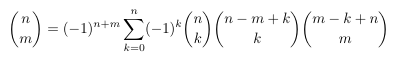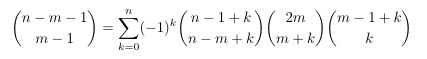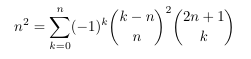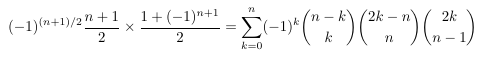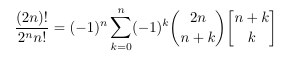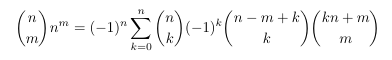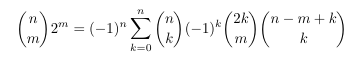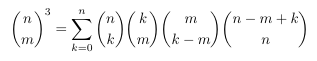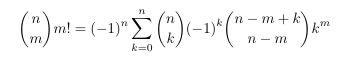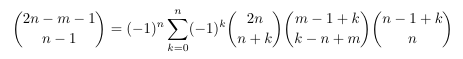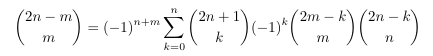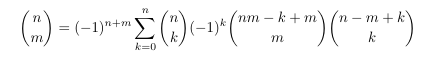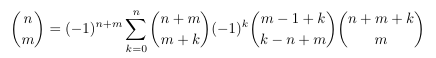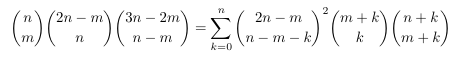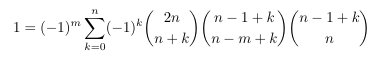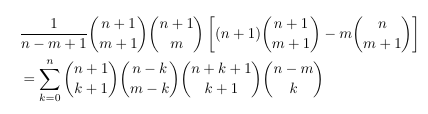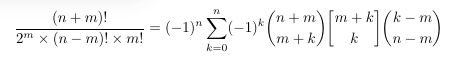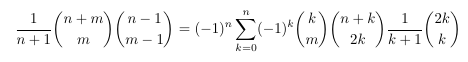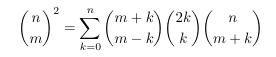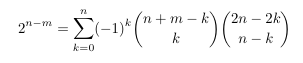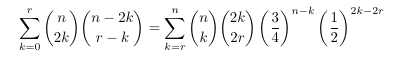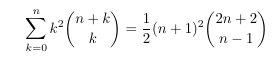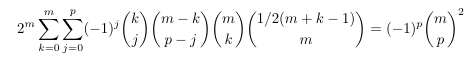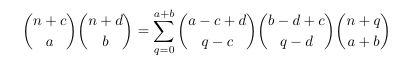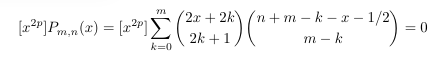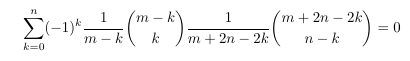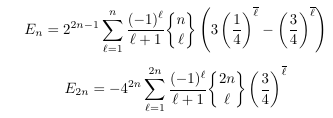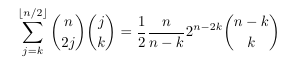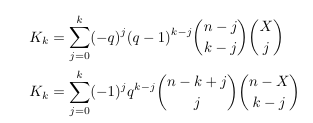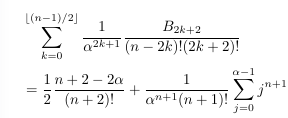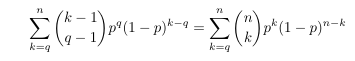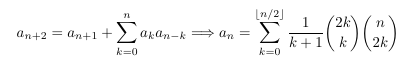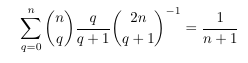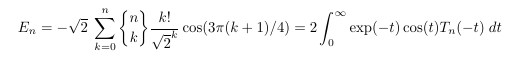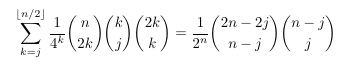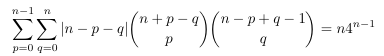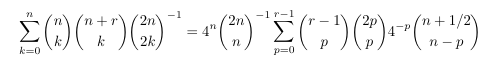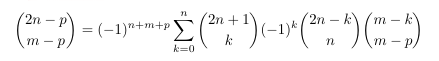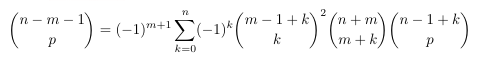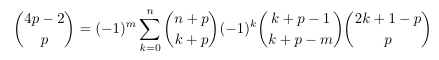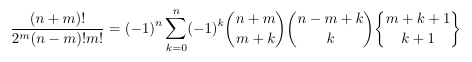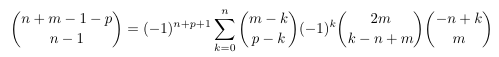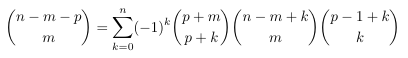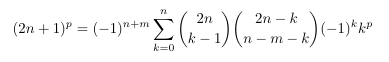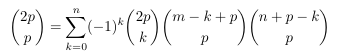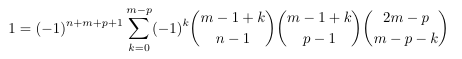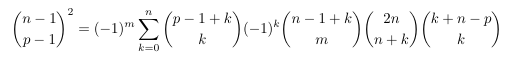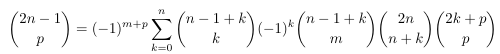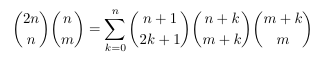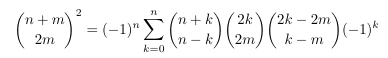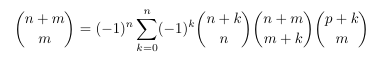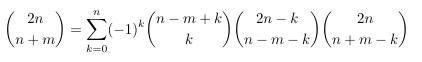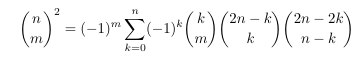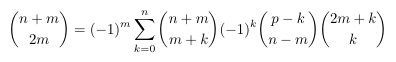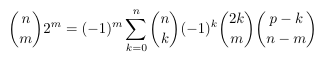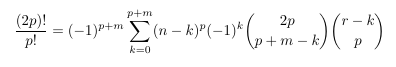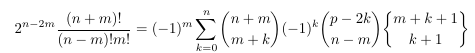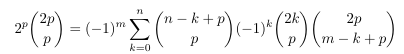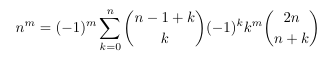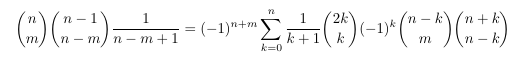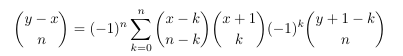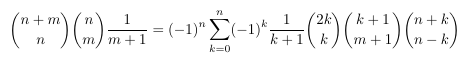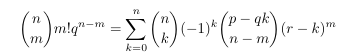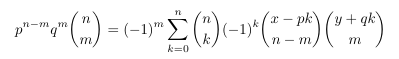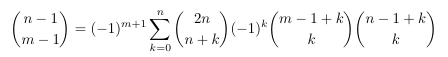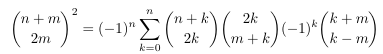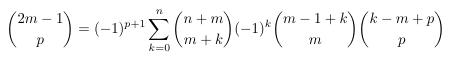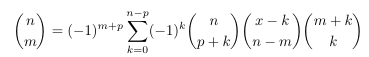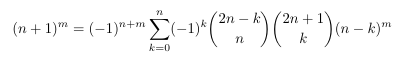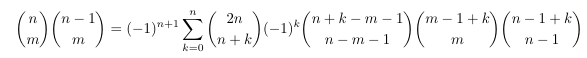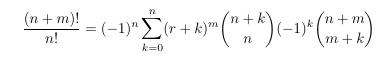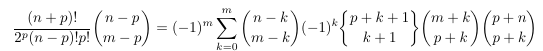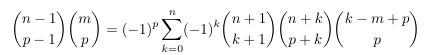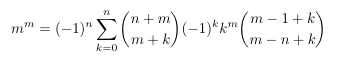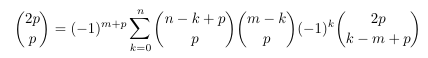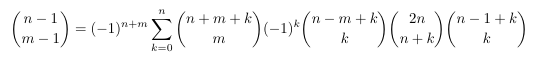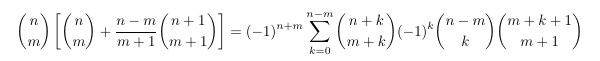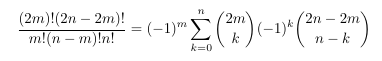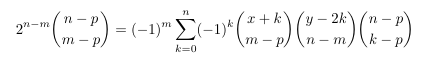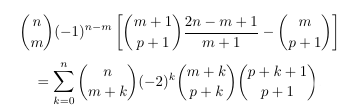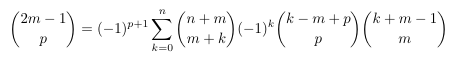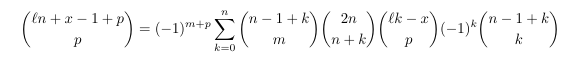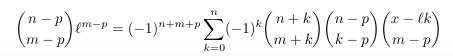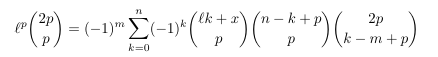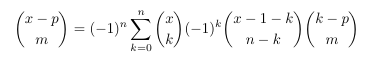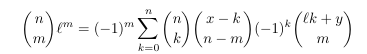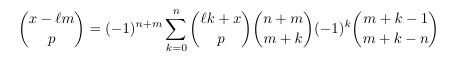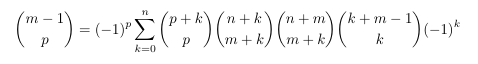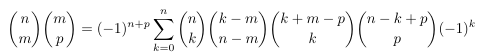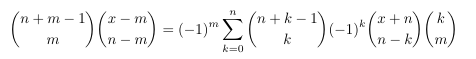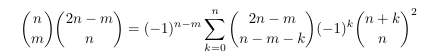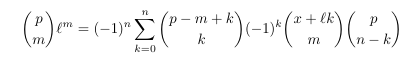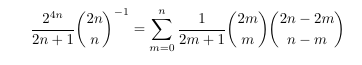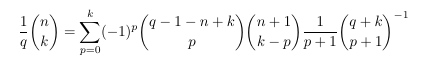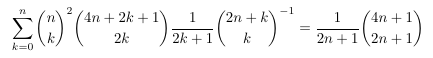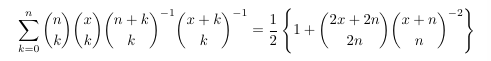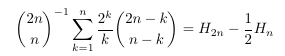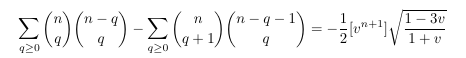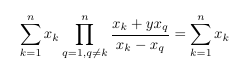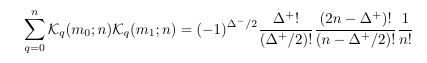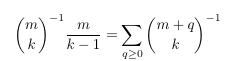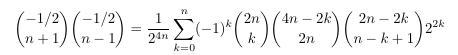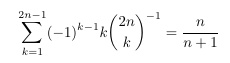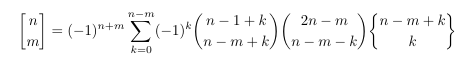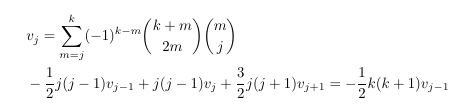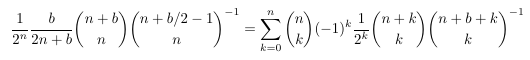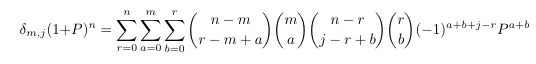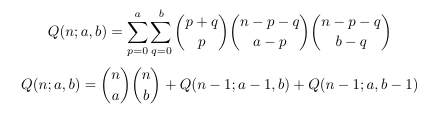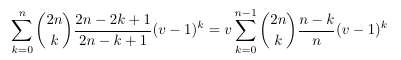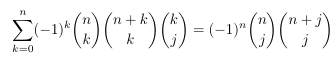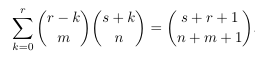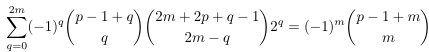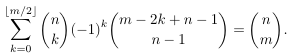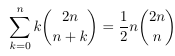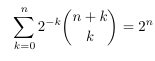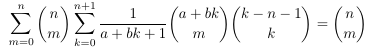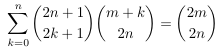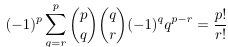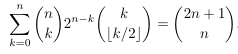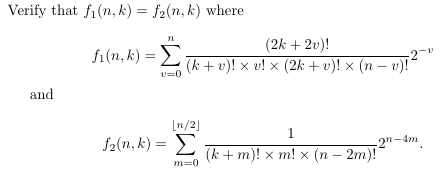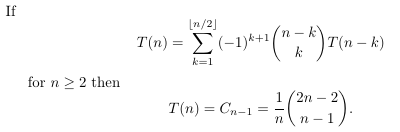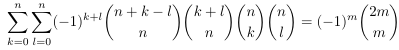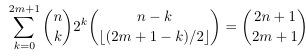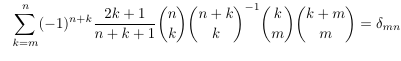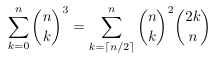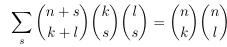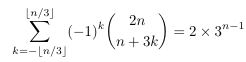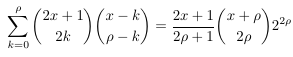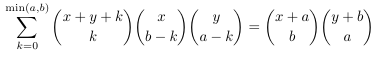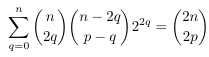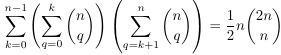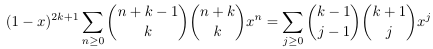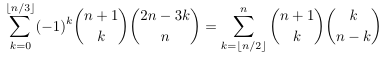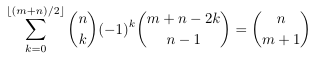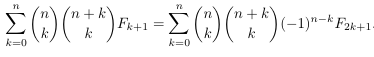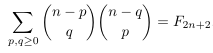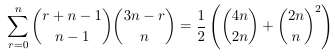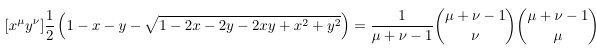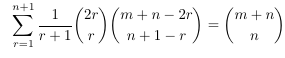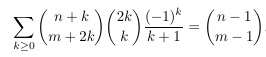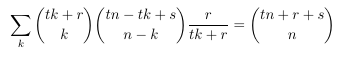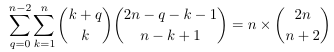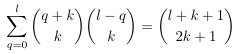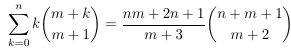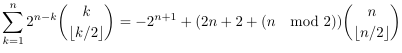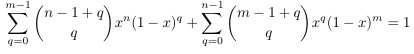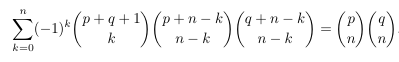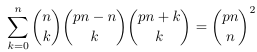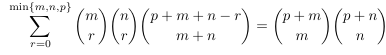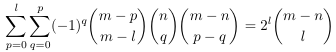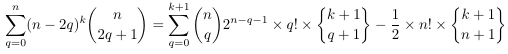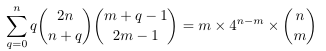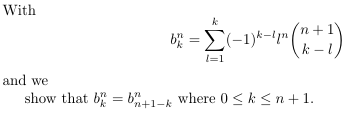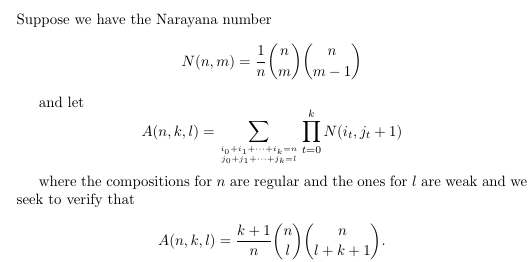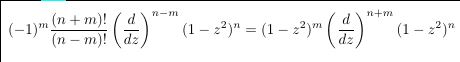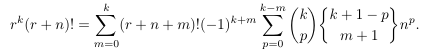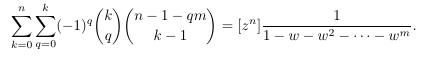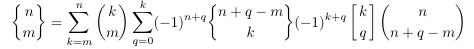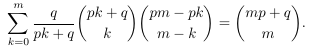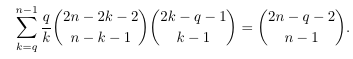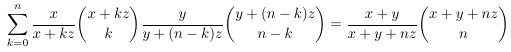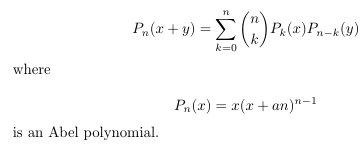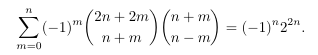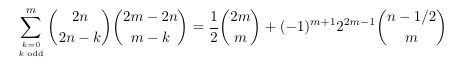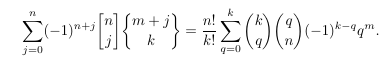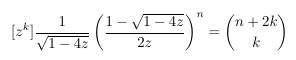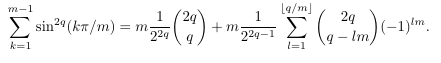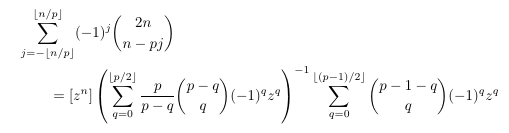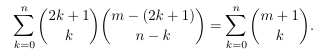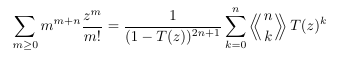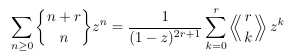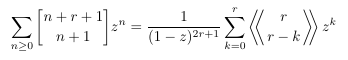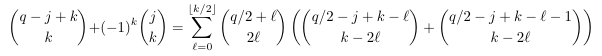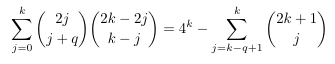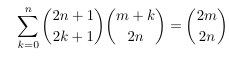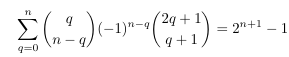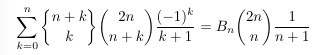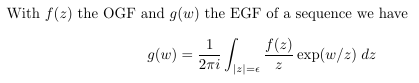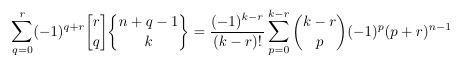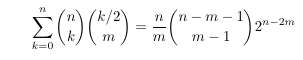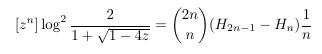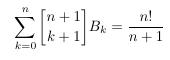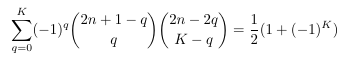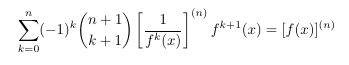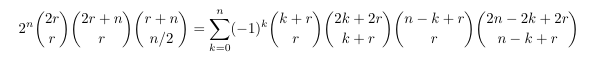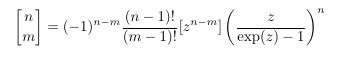Combinatorial numbers and Egorychev method
These are binomial coefficients, Stirling numbers, Catalan numbers,
Harmonic numbers, Eulerian numbers and Bernoulli numbers, as in
the book Integral representation and the Computation of
Combinatorial Sums by G. P. Egorychev.
The collection including a list of all identities proved is available
here (part 1 and 2, formal power series and residue operators):
and here (part 3, complex variables)
This includes a number of identities from
H.W. Gould's book Combinatorial identities
as well as L. Saalschütz's book on Bernoulli numbers.
We now have a new section as of March 2023 continuing to April
2025 "computer search" which includes hypergeometric identities that
can prove challenging even for computer algebra
systems, such as
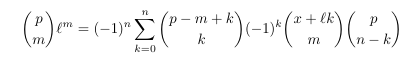
As of January 2024 "computer search" continues with rare identities
such as (the 42 identity)
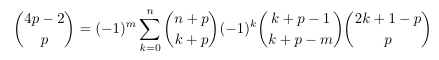
also featuring Narayana and Catalan numbers. These computer identities
have ranges of validity (boundary conditions) which are documented in
the text. These are in chronological order so that the most recent
work is at the end.
Here are the slides from Hosam Mahmoud's talk on Egorychev method
at Catholic University on November 9, 2022:
History and examples of
Egorychev method.
The 2023 paper "Egorychev method: a hidden treasure" by Riedel and
Mahmoud is at the following
Springer link.
My home page is here.
A MathJax version of this list can be
found here.
This is the list of identities in the above document, including
links to the posts where they first appeared.
Part 1 and 2
Egorychev method in formal power series
-
MSE 2384932
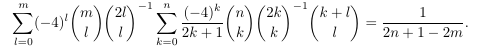
-
MSE 2472978
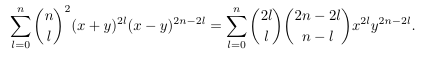
-
MSE 2719320
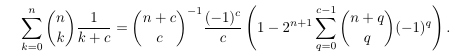
-
MSE 2830860
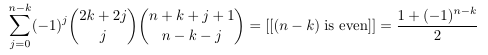
-
MSE 2904333
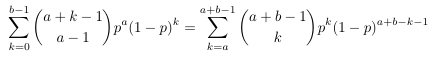
-
MSE 2950043
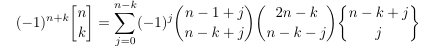
-
MSE 3049572
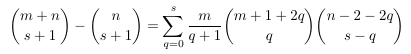
-
MSE 3051713
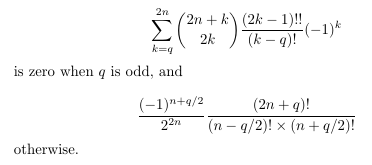
-
MSE 3068381
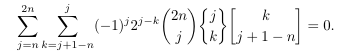
-
MSE 3138710
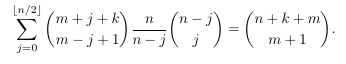
-
MSE 3196998
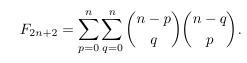
-
MSE 3245099
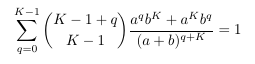
-
MSE 3260307
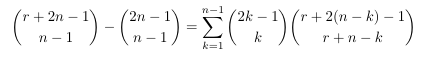
-
MSE 3285142
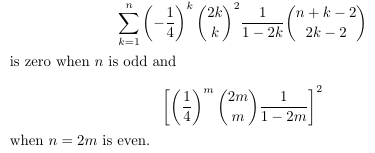
-
MSE 3333597
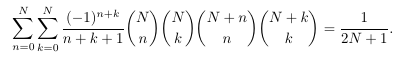
-
MSE 3342361
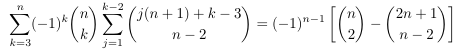
-
MSE 3383557
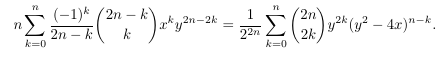
-
MSE 3441855
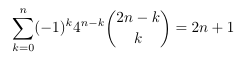
-
MSE 3577193
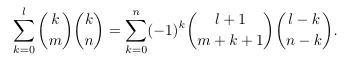
-
MSE 3583191
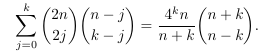
-
MSE 3592240
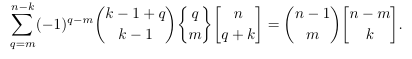
-
MSE 3604802
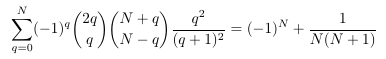
-
MSE 3619182
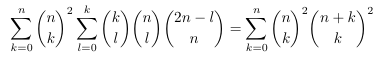
-
MSE 3638162
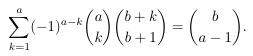
-
MSE 3661349
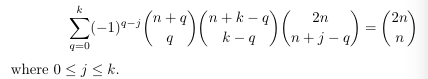
-
MSE 3706767
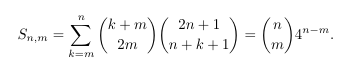
-
MSE 3737197
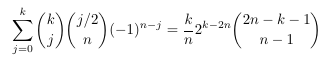
-
MSE 3825092
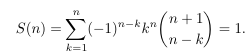
-
MSE 3845061
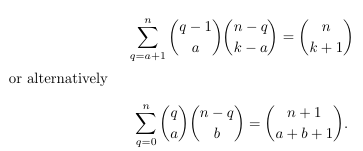
-
MSE 3885278
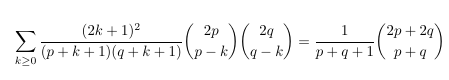
-
MSE 3559223
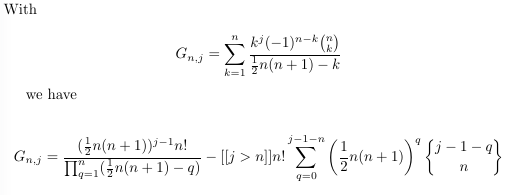
-
MSE 3926409
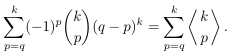
-
MSE 3942039
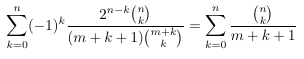
-
MSE 3956698
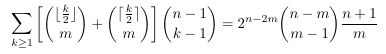
-
MSE 3993530
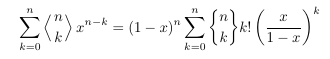
-
MSE 4008277
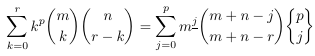
-
MSE 4031272 (Li Shanlan identity)
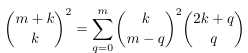
-
MSE 4034224 (Eulerian numbers, Stirling numbers first and second
kind)
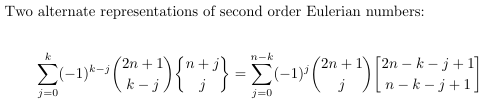
-
MSE 4037172 (Eulerian numbers, associated Stirling numbers first and
second kind)
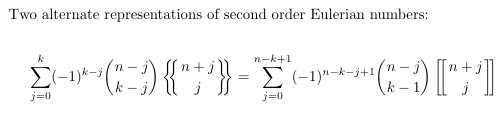
-
MSE 4037946 (Eulerian numbers, associated Stirling numbers first and
second kind)
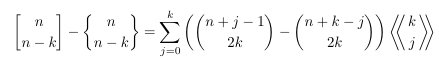
-
MSE 4055292
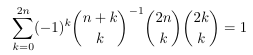
-
MSE 4054024
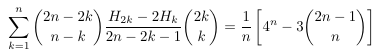
-
MSE 4084763
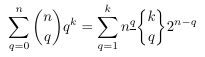
-
MSE 4095795
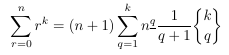
-
MSE 4098492
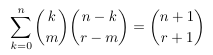
-
MSE 4127695
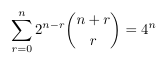
-
MSE 4131219
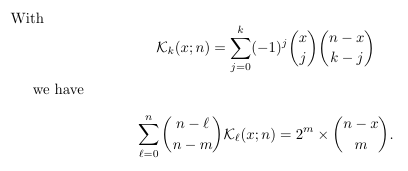
-
MSE 4139722
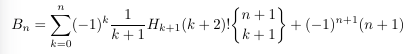
-
MSE 4192271
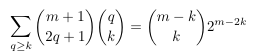
-
MSE 4212878
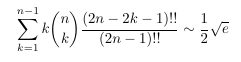
- A different obstacle from Concrete Mathematics by Knuth,
Graham, and Patashnik
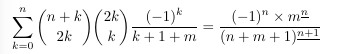
-
MO 291738 (not quite the same as previous)
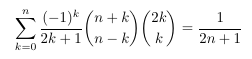
- A Stirling number identity by Gould
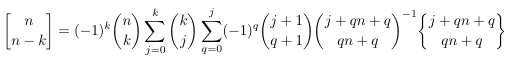
- A Stirling number identity by Gould II
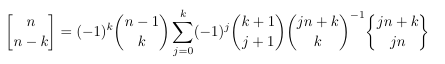
- Schläfli's identity for Stirling numbers

- Stirling numbers and Faulhaber's formula
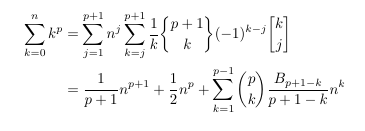
- Stirling numbers and binomial coefficient
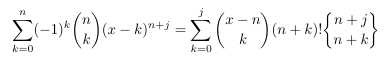
- Stirling numbers and a double binomial coefficient
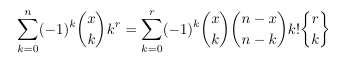
- Stirling numbers and a double binomial coefficient II
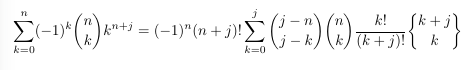
- Stirling numbers and Bernoulli polynomials
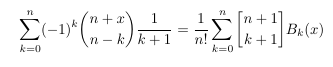
- Central binomial coefficients and Stirling numbers
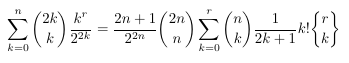
- Single variable monomial and two binomial coefficients
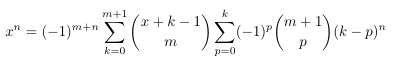
- Use of an Iverson bracket
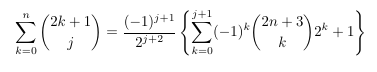
- Use of an Iverson bracket II
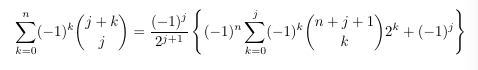
- Use of an Iverson bracket III
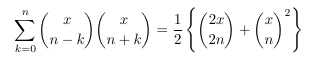
- Basic example
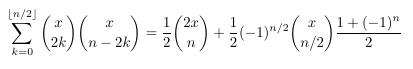
- Basic example continued
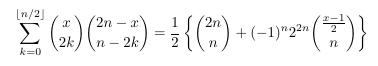
- An identity by Erik Sparre Andersen
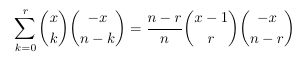
- Very basic example
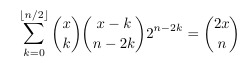
- An identity by Karl Goldberg
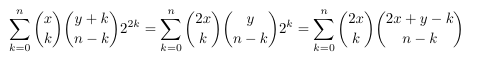
- Sum producing a square root
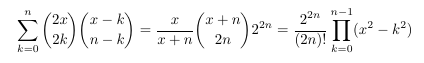
- Sum producing a square root II
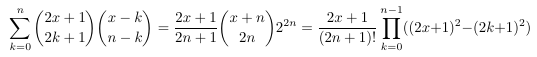
- Use of an Iverson bracket IV
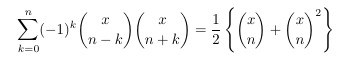
- Binomial coefficient manipulation
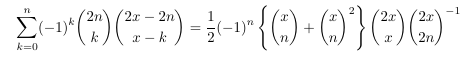
- Four binomial sums
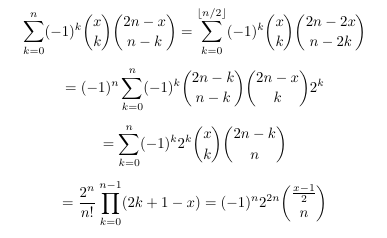
- Power term and two binomial coefficients
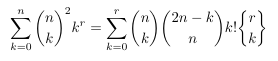
- Use of an Iverson bracket V
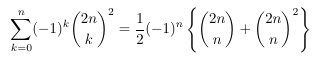
- Use of an Iverson bracket VI
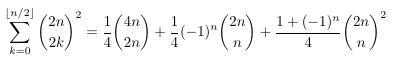
- Appearance of the constants three and five
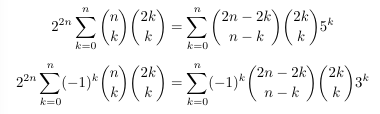
- Generating function of a binomial term
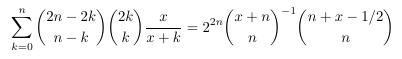
- Double square root
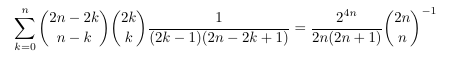
- Central Delannoy numbers
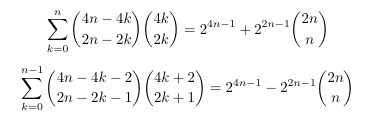
- A case of factorization
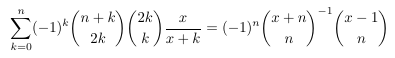
- Two identities due to Grosswald
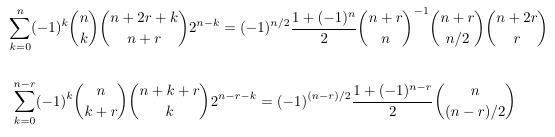
- Appearance of the constant three
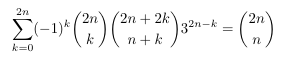
- Very basic example
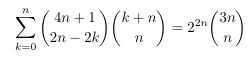
- Very basic example II
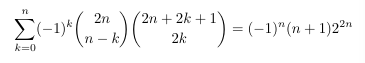
- Nested square root
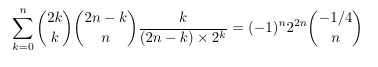
- Harmonic numbers and a squared binomial coefficient
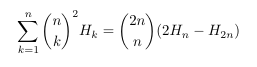
- Harmonic numbers and a double binomial coefficient
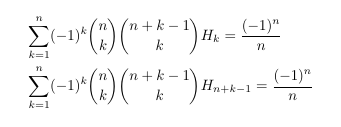
- Two instances of a Harmonic number
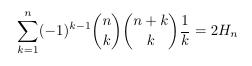
- Legendre Polynomials
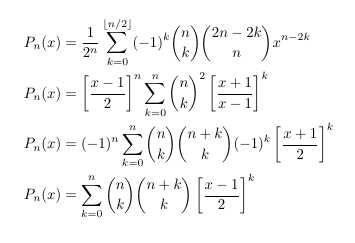
- Legendre Polynomials and a square root
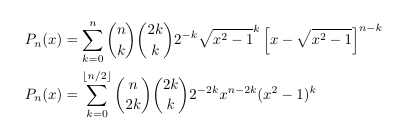
- Legendre Polynomials and a double square root
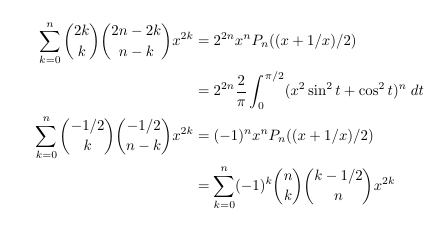
-
MSE 4304623
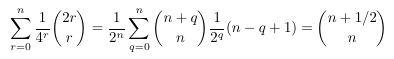
- Legendre Polynomials, trigonometric terms
and a contour integral
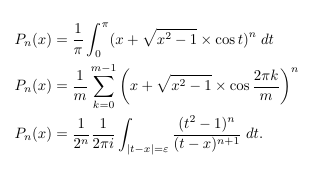
- Sum independent of a variable
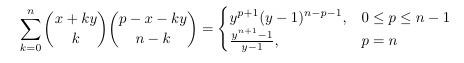
- Polynomial in three variables
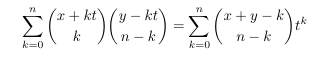
- An identity by Van der Corput
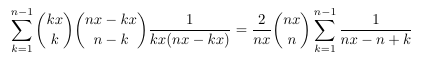
-
MSE 4316037 Logarithm, binomial coefficient and
harmonic numbers
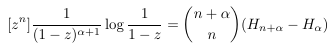
- An identity credited to Chung
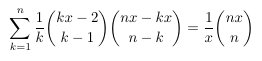
-
MSE 4317353 A Catalan number convolution
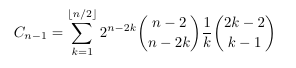
- Odd index binomial coefficients
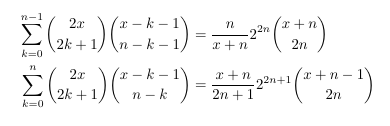
-
MSE 4325592 A sum of inverse binomial coefficients
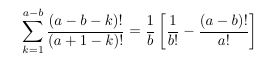
- Inverted sum index
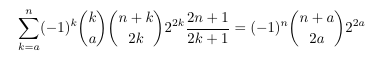
-
MSE 4351714 A Catalan number recurrence
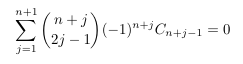
- An identity by Graham and Riordan
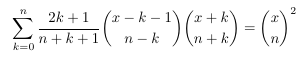
- Square root term
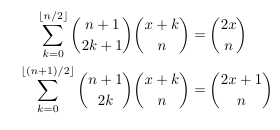
- An identity by Machover and Gould
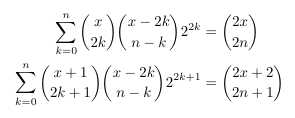
- Moriarty identity by H.T.Davis et al.
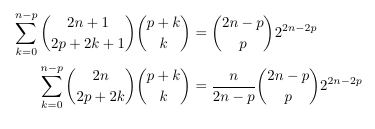
- Inverse Moriarty identity by Marcia Ascher.
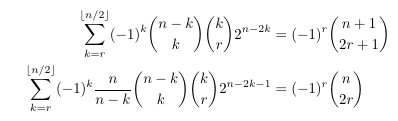
- Moriarty identity by Egorychev.
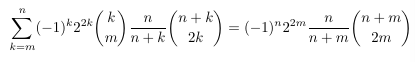
-
MSE 4462359 Two binomial coefficients
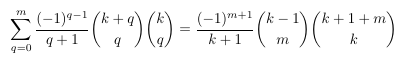
- Polynomial identity
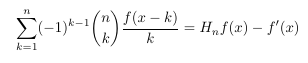
- Polynomial identity II
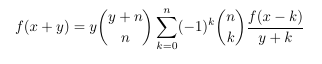
- Worpitzky-Nielsen series
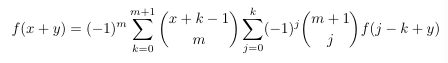
-
MSE 4517120 A sum of inverse binomial coefficients
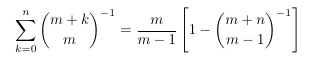
-
MSE 4520057 Symmetric Bernoulli number
identity
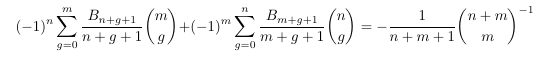
- Polynomial identity III
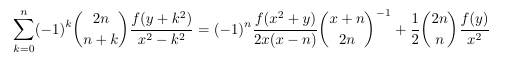
- Polynomial identity IV
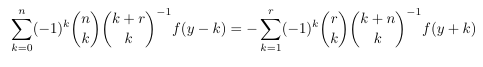
-
MSE 4540192 Symmetry in a simple proof
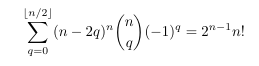
- Free functional term
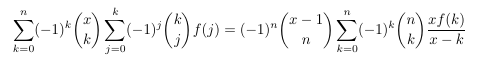
-
MSE 4547110 Inverse central binomial coefficient
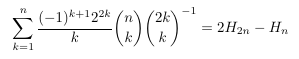
-
MSE 1402886 Inverse binomial coefficient
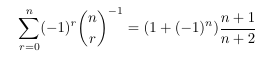
-
MSE 4552694 A pair of binomial transforms
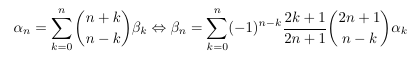
- Polynomial with inverse binomial coefficients
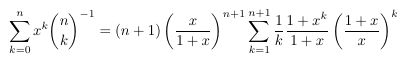
- Harmonic numbers with inverse binomial coefficients
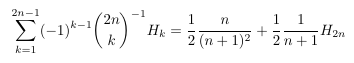
- Simon's identity
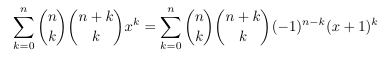
- Identity from Abramowitz and Stegun / Schläfli's
formula
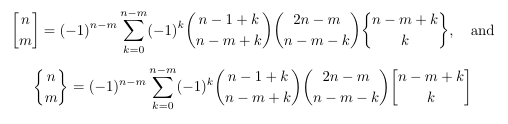
- Bernoulli / Stirling number identity
identity
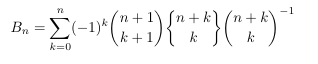
- Recurrence relation from DLMF
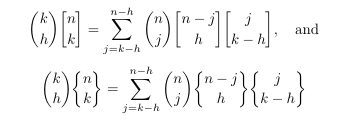
- Bernoulli, Fibonacci and Lucas numbers
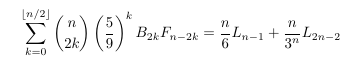
- Bernoulli / exponential convolution
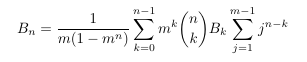
- Bernoulli identity by Munch
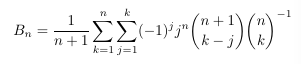
- Bernoulli identity by Kronecker
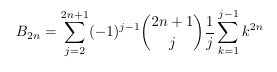
- Computing Bernoulli numbers
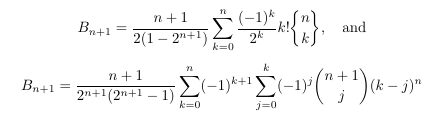
From the Saalschütz text
- Bernoulli numbers I
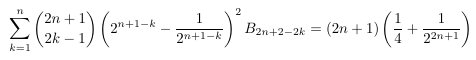
- Bernoulli numbers II
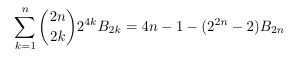
- Bernoulli numbers III
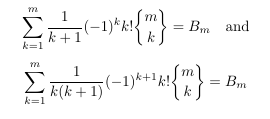
- Bernoulli numbers IV
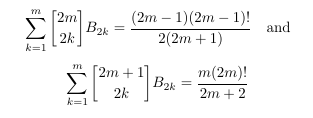
- Bernoulli and Eulerian numbers I
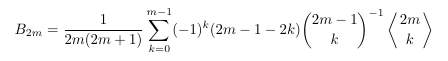
- Bernoulli and Eulerian numbers II
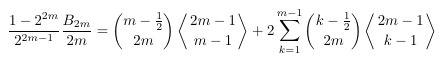
- Bernoulli numbers V
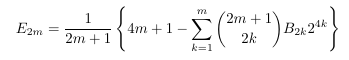
- Bernoulli numbers and roots of unity
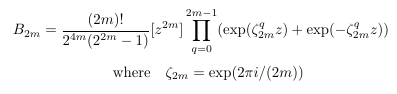
- Worpitzky's identity
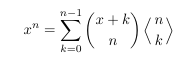
-
MSE 4627726: Quadruple binomial coefficient
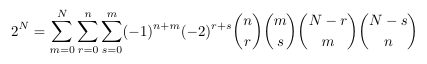
-
MSE 4627918: Alternating power sum
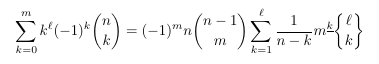
-
MSE 4227433: Squared power sum
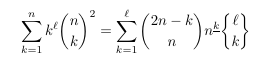
-
MSE 4428892: Ordinary power sum
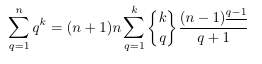
-
MSE 3932757: Stirling numbers and a tree-function like term
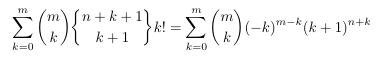
-
MSE 4641290: A vanishing variable
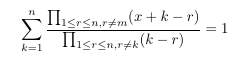
-
MSE 4644963: From trigonometric to rational
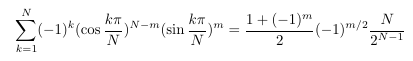
-
MSE 4657112: Triple combinatorial numbers to
constant
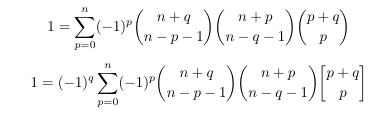
Computer search
-
MSE 4667102: Two different representations of a coefficient
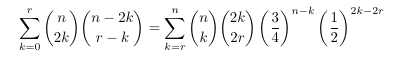
-
MSE 4675665: Rational term of constant degree
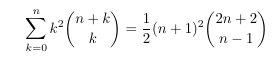
-
MSE 4666141: Double square root
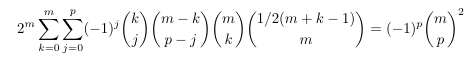
-
MSE 4699857: Four auxiliary variables
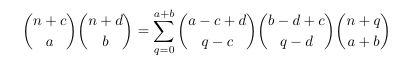
-
MSE 4703564: A family of odd polynomials
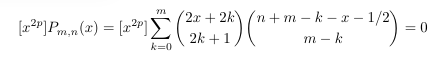
-
MSE 4713851: A sum with a zero value
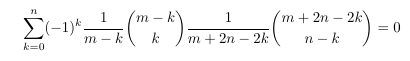
-
MSE 4722503: Euler numbers and Stirling numbers
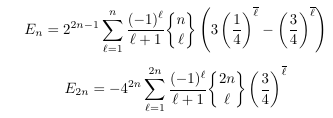
-
MSE 495371: Even-index binomial
coefficient convolution
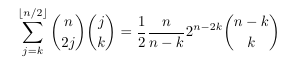
-
MSE 4731417: Kravchuk polynomials
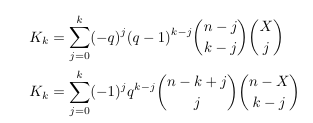
-
MSE 4762542: Binomial-Bernoulli convolution
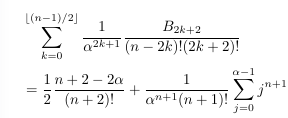
-
MSE 4774167 : Two probabilities
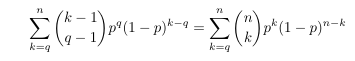
-
MSE 4791957 : Motzkin numbers
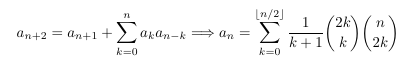
-
MSE 4821034 : An inverse binomial coefficient
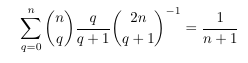
-
MSE 4830342 : Euler numbers, Stirling numbers and Touchard
polynomials
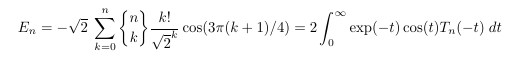
-
MSE 4832009 : A triple binomial
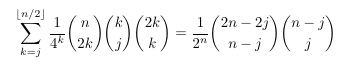
-
MSE 4843051 : Double sum with an absolute value
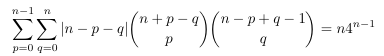
-
MSE 4850609 :Inverse central binomial coefficient in sum
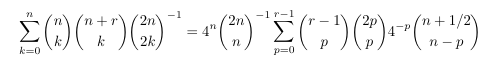
Computer search II
-
MSE 4902676: Inverse central binomial coefficient
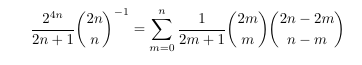
-
MSE 4906245: Another inverse binomial coefficient
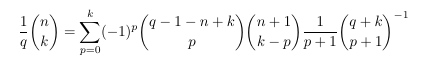
- Quadruple hypergeometric with an inverse
binomial coefficient
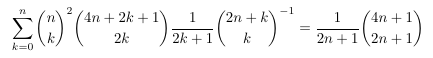
- Quadruple hypergeometric with two inverse
binomial coefficients
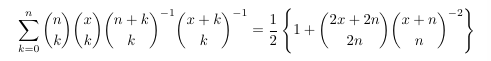
-
MSE 4949815: Inverse binomial coefficient with harmonic numbers
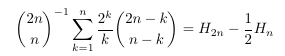
-
MSE 4960823: Binomial coefficient scaled power sum

- MSE
4964157: Two central binomial coefficients and a fractional
term

- MSE
4976413: Riordan number asymptotics from central trinomial
coefficients
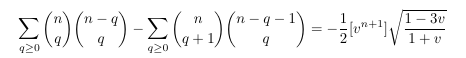
- MSE
4980771: Polynomials and the residue at infinity
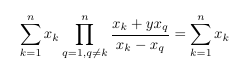
- MSE
4980771: Kravchuk polynomial and Vandermonde convolution
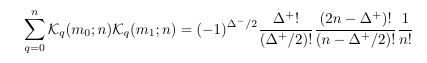
- MSE
5003960: A sum of a certain hypergeometric term
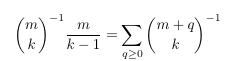
- MSE
5010757: Triple hypergeometric with two square root terms
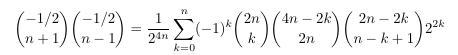
- MSE
4989609: An inverse binomial coefficient
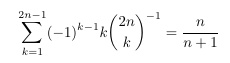
- Both types of Stirling numbers and the logarithm identity
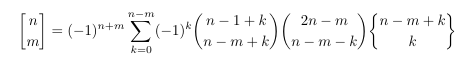
- MSE
5030526: A triple sum identity
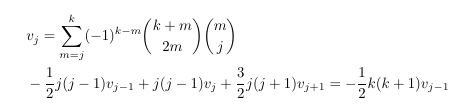
- A triple hypergeometric and the logarithm identity
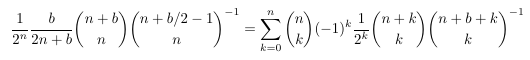
- MSE
5030526: An iterated sum identity
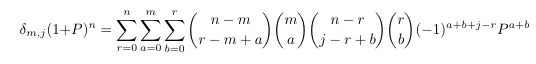
- MSE
5041394: Recurrence for a triple hypergeometric
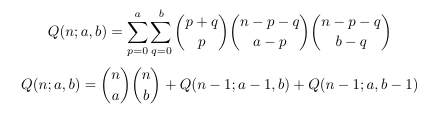
- MSE
5070518: Polynomial identity by McKay
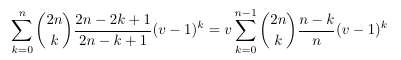
Part 3
Egorychev method in complex variables
- Introductory
example for the method
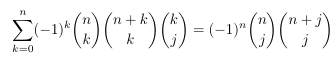
- Introductory
example for the method, convergence about zero
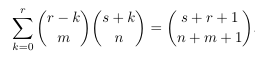
- Introductory
example for the method, an interesting substitution
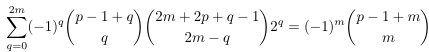
- Introductory
example for the method, another interesting substitution
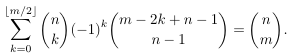
- Introductory
example for the method, yet another interesting substitution
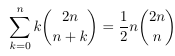
- Using
an Iverson bracket only
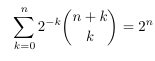
- Verifying
that a certain sum vanishes
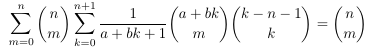
- A case
of radical cancellation
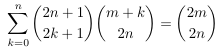
- Basic
usage of exponentiation integral
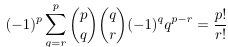
- Introductory
example for the method, eliminating odd-even dependence
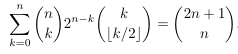
- Introductory
example for the method, proving equality of two double
hypergeometrics
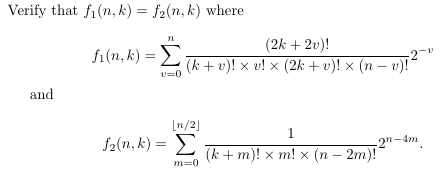
- A
remarkable case of factorization
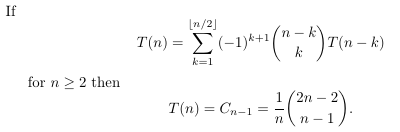
- Evaluating
a quadruple hypergeometric
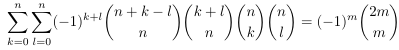
- An
integral representation of a binomial coefficient involving the floor
function
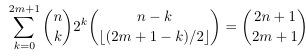
- Evaluating
another quadruple hypergeometric
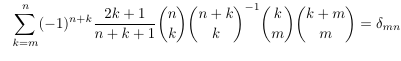
- An
identity by Strehl
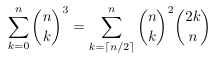
- Shifting
the index variable and applying Leibniz' rule
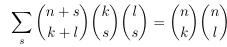
- Working
with negative indices
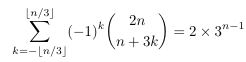
- Two
companion identities by Gould
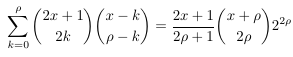
- Exercise
1.3 from Stanley's Enumerative Combinatorics
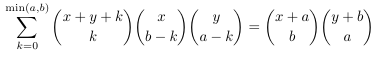
- Counting
m-subsets
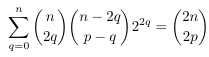
- Method
applied to an iterated sum
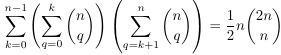
- A pair
of two double hypergeometrics
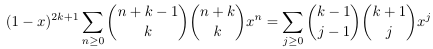
- A two
phase application of the method
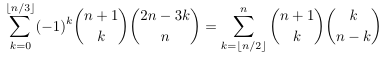
- An
identity from Mathematical Reflections
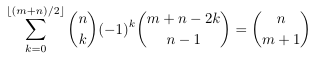
- A triple
Fibonacci-binomial coefficient convolution
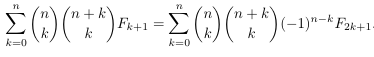
- Fibonacci
numbers and the residue at infinity
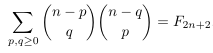
- Permutations
containing a given subsequence
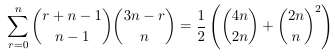
- An
example of Lagrange inversion
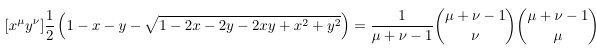
- A
binomial coefficient - Catalan number convolution
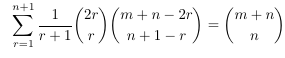
- A new obstacle from Concrete Mathematics
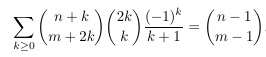
- Abel-Aigner
identity from Table 202 of Concrete Mathematics
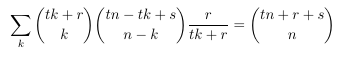
- Reducing
the form of a double hypergeometric
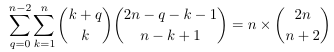
- Basic
usage of the Iverson bracket
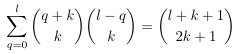
- Basic
usage of the Iverson bracket II
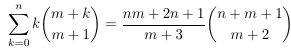
- Use of
a double Iverson bracket
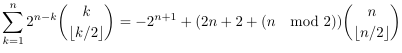
- Iverson
bracket and an identity by Gosper, generalized
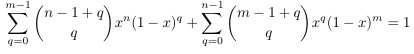
- Factoring
a triple hypergeometric sum
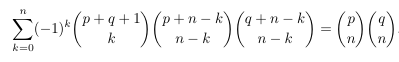
- Factoring
a triple hypergeometric sum II
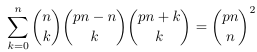
- Factoring
a triple hypergeometric sum III
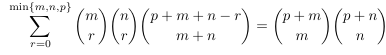
- A
triple hypergeometric sum IV
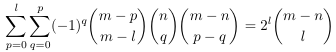
- Basic
usage of exponentiation integral to obtain Stirling number
formulae
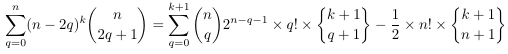
- Three
phase application including Leibniz' rule
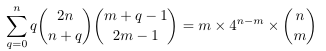
- Symmetry
of the Euler-Frobenius coefficient
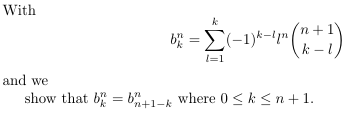
- A
probability distribution with two parameters

- An
identity involving Narayana numbers
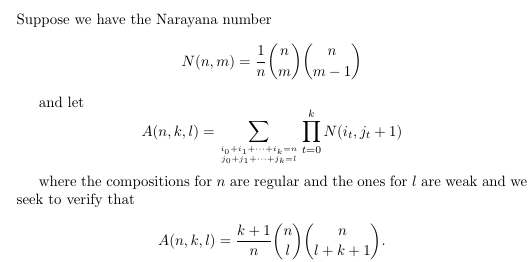
- Convolution
of Narayana polynomials

- A
property of Legendre polynomials
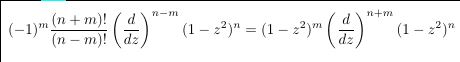
- A sum
of factorials, OGF and EGF of the Stirling numbers of the second
kind
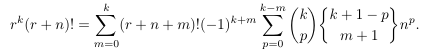
- Fibonacci,
Tribonacci, Tetranacci
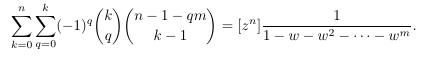
- Stirling
numbers of two kinds, binomial coefficients
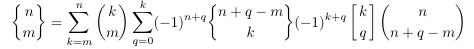
- An
identity involving involving two binomial coefficients and a
fractional term
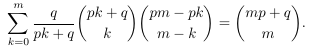
- Double
chain of a total of three integrals
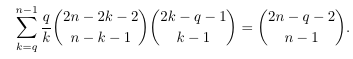
- Rothe-Hagen
identity
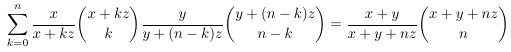
- Abel
polynomials are of binomial type
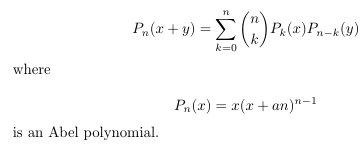
- A
summation identity with four poles
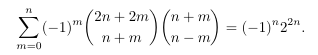
- A
summation identity over odd indices with a branch cut
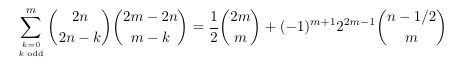
- A
Stirling-number identity
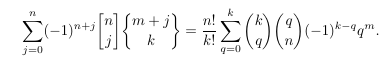
- A
Catalan-Central binomial coefficient convolution
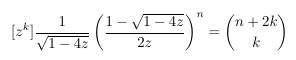
Post Scriptum section
- A
trigonometric sum
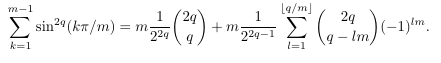
- A
class of polynomials similar to Fibonacci and Lucas
Polynomials
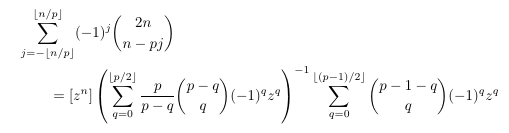
-
Partial row sums in Pascal's triangle
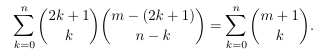
- The
tree function and Eulerian numbers of the second order
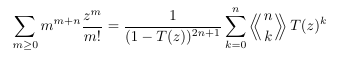
- A
Stirling set number generating function and Eulerian numbers of the
second order
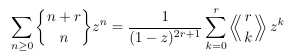
A Stirling
cycle number generating function and Eulerian numbers of the second
order (II)
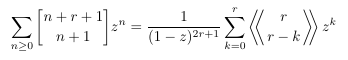
- Another
case of factorization
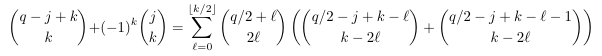
- An
additional case of factorization
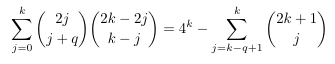
- Contours
and a binomial square root
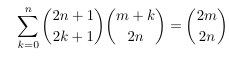
- A
careful examination of contours
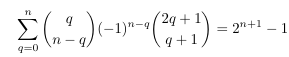
- Stirling numbers, Bernoulli numbers and Catalan
numbers from Concrete Mathematics by Graham, Knuth and
Patashnik
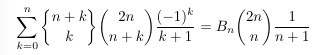
- Transforming
an OGF into an EGF
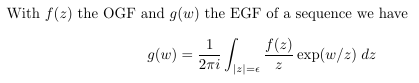
- Stirling numbers of the first and second kind
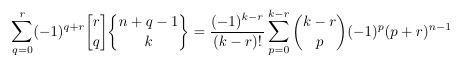
- An identity by Carlitz
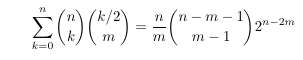
- Logarithm
of the Catalan number OGF
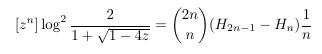
- A Bernoulli / Stirling number identity
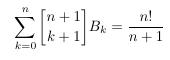
- Formal
power series vs contour integration
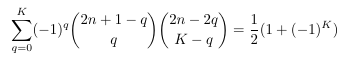
- A sum
of the derivatives of inverse powers
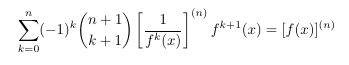
- Shifted central binomial coefficient convolution
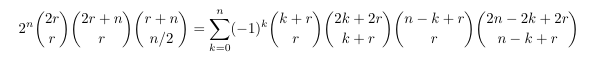
- Stirling
cycle numbers and an exponential EGF
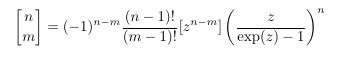
Computer search III