Willkommen zu 2025!

Sie sind fasziniert von dem rechts gezeigten Zahlenzauber? Sie folgen neugierig dem QR-Link und wollen mehr wissen? Sehr gerne, hier sind Sie richtig. Diese Webseite erklärt die Mathematik hinter unserem Poster 2025 und was wir uns dabei gedacht haben.

Wissbegier und Lernfreude sind etwas Schönes. Sie überlegen sogar, Mathematik zu studieren? Mehr zum Mathestudium erfahren Sie auf den Seiten des Fachbereichs Mathematik der Universität Stuttgart. Hilfreich ist auch die Seite Mathe Studieren?! der DMV.

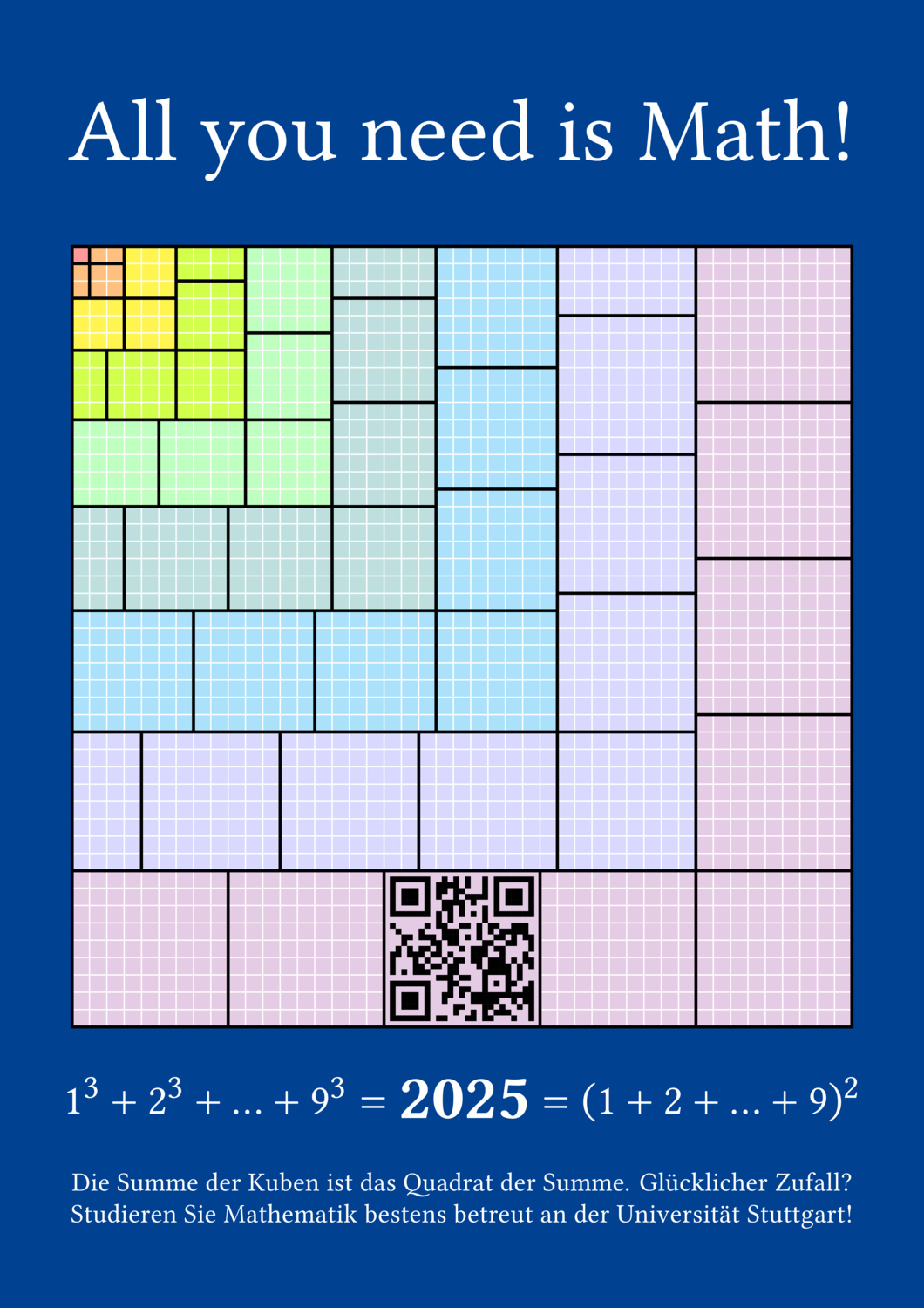
Die Summe der Kuben ist das Quadrat der Summe.

Die Zahl 2025 ist tatsächlich ein glücklicher Zufall und unser aktueller Anlass; weitere tausend Jahre bis 3025 wollten wir mit unserem Poster nicht warten! Doch hinter der gezeigten Gleichung \( 1^3 + 2^3 + \ldots + 9^3 = (1+2+\ldots+9)^2 \) steckt eine wunderbare Erkenntnis, eine allgemeine Gesetzmäßigkeit, für „beliebige Werte von Neun“. Dieses verblüffende Theorem wird vom Poster feierlich visualisiert, als Beweis ohne Worte, und auf dieser Webseite erläutert.

Das Poster zeigt oben links \(1^3 + 2^3 = (1+2)^2\) in rot und orange. Für \(1^3 + 2^3 + 3^3 = (1+2+3)^2\) kommt gelb hinzu, für \(1^3 + 2^3 + 3^3 + 4^3 = (1+2+3+4)^2\) grün. Das sind schon \(100\) Kästchen, doch als \(10 \times 10\) – Quadrat angordnet wird alles einfach und übersichtlich. Das Muster setzt sich fort bis zum Gesamtkunstwerk \( 1^3 + 2^3 + \ldots + 9^3 = (1+2+\ldots+9)^2 \). So lässt sich die Summe der Kuben leicht ausrechnen, sogar im Kopf, als Quadrat der Summe, hier also \(45^2 = 2025\). Voilà!

C'est par la logique que l'on prouve
et par l'intuition que l'on découvre.
— Mit der Logik beweisen wir,
mit der Intuition entdecken wir.
Henri Poincaré (1854–1912)

Geht das immer so weiter?

Mathematische Induktion zeigt, dass wir auf einer Leiter
so hoch klettern können wie wir nur wollen, sobald wir auf
die erste Sprosse gelangen können (als Induktionsanfang)
und von jeder Sprosse zur nächsten (als Induktionsschritt).
Donald Knuth, Concrete Mathematics

Das hier gezeigte Muster können wir beliebig fortsetzen. Visuell ist das sofort plausibel. Mit etwas Geschick und der allseits beliebten binomischen Formel können Sie dies selbst nachrechnen und sogar beweisen: In Schule und Studium lernt man hierzu die Technik der Induktion. Diese Strategie ist erfreulich einfach und oft erfolgreich!

Für jede natürliche Zahl \(n = 1,2,3,\ldots\) gilt also tatsächlich die wunderschöne Gleichung \(1^3 + 2^3 + \ldots + n^3 = (1+2+\ldots+n)^2\). Diese frappierende Erkenntnis geht wohl zurück auf Nikomachos von Gerasa, einen Philosophen und Mathematiker des 1./2. Jahrhunderts unserer Zeit.

Mathematik ist immer beides, sowohl abstrakte Erkenntnis als auch konkrete Anwendung. Beide ergänzen sich und abeiten effizient zusammen, wie linke und rechte Hand. Genau das lernen Sie im Studium, Wissen und Können.

Der kleine Gauß

Wenn Sie ganz genau hinschauen, dann zeigt Ihnen das Poster zudem als Dreingabe \( 1+2+\ldots+n = n(n+1)/2 \). Das ist die noch berühmtere Gaußsche Summenformel. Alles in einer Graphik. Hoch lebe 2025!

Mathematics is the science of the infinite.
Hermann Weyl, Levels of Infinity