- T.
Weidl: ``Some general operator ideals of the weak type'',
(Russian) Algebra i Analiz, 4, 3 (1992) 117-144, (English) AMS
St.-Petersburg Mathematical Journal, 4, 3 (1993) 503-525.
- T.
Weidl: ``Estimates for operators of the type b(x)a(D) in
non-powerlike ideals'', (Russian) Algebra i Analiz, 5, 5 (1993)
48-67, (English) AMS St.-Petersburg Mathematical Journal 5, 5
(1994) 907-923.
- M.
Sh. Birman, T. Weidl: ``The discrete spectrum in a gap of the
continuous one for compact supported perturbations'', Operator
Theory: Advances and Applications, 70 (1993) 9-12.
- T.
Weidl: ``Cwikel type estimates in nonpower ideals'',
Mathematische Nachrichten, 176 (1995) 315-334.
- T.
Weidl: ``On the Lieb-Thirring constants
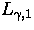 for
for
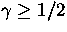 '',
Communications in Mathematical Physics, 178, 1 (1996) 135-146. '',
Communications in Mathematical Physics, 178, 1 (1996) 135-146.
- Y.
Netrusov, T. Weidl: ``On Lieb-Thirring inequalities for higher
order operators with critical and subcritical powers'',
Communications in Mathematical Physics, 182, (1996) 355-370.
- I.
Roitberg, D. Vassiliev, T. Weidl: ``Edge resonance in an elastic
semi-strip'', Quaterly Journal of Mechanics and Applied
Mathematics, 51 (1998) 1-13.
- T.
Weidl: ``Eigenvalue asymptotics for locally perturbed second
order differential operators'', Journal of the London
Mathematical Society 57 1 (1999) 227-251.
- T.
Weidl: ``Remarks on virtual bound states for semi-bounded
operators'', Communications in Partial Differential Equations 24
1&2 (1999) 25-60.
- T.
Weidl: ``Another look at Cwikel's inequality'', in Differential
Operators and Spectral Theory. M.Sh. Birman's 70th Anniversary
Collection. AMS Translations Series 2 189 (1999) 247-254.
- A.
Laptev, T. Weidl: ``Hardy inequalities for magnetic Dirichlet
forms'', Operator Theory: Advances and Applications 108 (1999)
299-305.
- T.
Weidl: ``A Remark on Hardy type inequalities for critical
Schrödinger operators with magnetic fields'', Operator
Theory: Advances and Applications 110 (1999) 345-352.
- A.
Laptev, T. Weidl: ``Sharp Lieb-Thirring Inequalities in High
Dimensions'', Acta Mathematica 184 (2000) 87-111.
- D.
Hundertmark, A. Laptev, T. Weidl: ``New bounds on the
Lieb-Thirring constants'', Inventiones mathematicae 140 3 (2000)
693-704.
- A.
Laptev, T. Weidl: ``Recent results on Lieb-Thirring
inequalities'', Proceedings Journees EDP 5-9 juin 2000 (2000)
XX-1 - XX-14
- P.
Exner, T. Weidl: ``Lieb-Thirring Inequalities on Trapped Modes in
Quantum Wires'', XIIIth International Congress on Mathematical
Physics (London, 2000), 437-443, Int. Press, Boston, MA, 2001.
- A.
Laptev, O. Safronov, T. Weidl: ``Bound state asymptotics for
elliptic operators with strongly degenerated symbols'', Nonlinear
problems in mathematical physics and related topics, I, In Honor
of Professor O. A. Ladyzhenskaya. 233-246, Int. Math. Ser. (N.
Y.), 1, Kluwer/Plenum, New York, 2002.
- S. Vugalter, T.
Weidl: ``On the Discrete Spectrum of a Pseudo-Relativistic
Two-Body Pair Operator'', Ann. Henri Poincaré 4 (2003),
no. 2, 301-341.
- P. Exner, H. Linde, T.
Weidl: ``Lieb-Thirring inequalities for
geometrically induced bound states'', Lett. Math. Phys. 70 (2004),
no. 1, 83-95.
-
Spectral analysis of partial
differential equations.
Abstracts from the workshop held
November 28--December 4, 2004.
Organized by Alexander V. Sobolev and
Timo Weidl.
Oberwolfach Reports. Vol. 1, no. 4.
Oberwolfach Rep. 1 (2004), no. 4, 2839--2911.
- C. Förster, T. Weidl:
``Trapped modes for an elastic strip with
perturbation of the material properties'',
Quarterly Journal of Mechanics and
Applied Mathematics 2006 59(3), 399-418.
- T. Weidl: ``Nonstandard Cwikel
Type Estimates''. 337--357,
Contemp. Math., 445, Amer. Math. Soc., Providence, RI, 2007.
- H. Kovarik, S. Vugalter,
T. Weidl:
``Spectral estimates for two-dimensional
Schrödinger operators with
application to quantum
layers''. Comm. Math. Phys. 275
(2007),
no. 3, 827--838.
-
R. L. Frank, B. Simon, T. Weidl:
``Eigenvalue Bounds for Perturbations of
Schrödinger Operators and Jacobi Matrices With Regular Ground
States.'' Comm.
Math. Phys. 278 (2008), no. 1, 199--208.
-
T. Weidl:
``Improved Berezin-Li-Yau inequalities with
a remainder term'', in Spectral Theory of
Differential Operators, Amer. Math. Soc. Transl. (2) 225
(2008), 253--263.
-
R. L. Frank, M. Loss, T. Weidl:
``Polya's Conjecture in the Presence of a Constant Magnetic Field''.
JEMS 11 (2009) 1365-1383.
- H. Kovarik, S. Vugalter,
T. Weidl:
``Two-dimensional Berezin-Li-Yau inequalities with a correction term''.
Comm. Math. Phys. 287 (2009) no. 3, 959--981.
-
Low eigenvalues of Laplace and Schrödinger operators. Abstracts from the
workshop held February 8--14, 2009. Organized by Mark Ashbaugh, Rafael Benguria,
Richard Laugesen and Timo Weidl. Oberwolfach Reports. Vol. 6, no.1 (2009)
355-427.
-
L. Geisinger,
T. Weidl:
``Universal bounds for traces of the
Dirichlet Laplace operator''.
Journal of the London Mathematical
Society 82 (2010) (2) 395-419.
-
A. Laptev, L. Geisinger,
T. Weidl:
``Geometrical versions of improved
Berezin-Li-Yau inequalities''.
Journal of Spectral Theory 1 (2011), 87-109.
-
T. Weidl:
``Semiclassical Spectral Bounds and
Beyond''. in Mathematical results in quantum physics, 110-129,
World Sci. Publ., Hackensack, NJ, 2011
-
L. Geisinger,
T. Weidl:
``Sharp spectral estimates in domains of infinite volume''. Reviews in Mathematical Physics 23 (2011) (6) 615-641.
-
C. Förster, T. Weidl:
``Trapped modes in an elastic plate
with a hole'' (Russian).
Algebra i Analiz 23 (2011) (1) 255-288. English translation in St. Petersburg Math. J. 23 (2012) (1) 179-202.
-
H. Kovarik,
T. Weidl:
``Improved Berezin-Li-Yau inequalities
with magnetic fields''. Proceedings of the Royal Society of
Edinburgh, 145A, 145-160, 2015.
-
D. Barseghyan,
P. Exner,
H. Kovarik,
T. Weidl:
``Semiclassical bounds
in magnetic bottles''. Reviews in Mathematical Physics, 28 (1) 2016.
http://dx.doi.org/10.1142/S0129055X16500021 29pp.
-
A. Hänel,
T. Weidl:
``Eigenvalue asymptotics for an
elastic strip and an elastic plate
with a crack''.
Quaterly Journal of Mechanics and Applied
Mathematics, 69 (4) 319-352, 2016.
-
A. Hänel,
T. Weidl:
``Spectral asymptotics for the Dirichlet Laplacian with a Neumann window via a Birman-Schwinger analysis of the Dirichlet-to-Neumann operator''. in
Functional Analysis and Operator
Theory for Quantum Physics, EMS Series
of Congress Reports, J. Dittrich, et
al. (eds.), 315-352, 2017.
-
H. Kovarik, B. Ruszkowski,
T. Weidl:
``Spectral estimates for the Heisenberg
Laplacian on cylinders''. in
Functional Analysis and Operator
Theory for Quantum Physics, EMS Series
of Congress Reports, J. Dittrich, et
al. (eds.), 433-446, 2017.
-
H. Kovarik, B. Ruszkowski,
T. Weidl:
``Melas-type bounds for the Heisenberg
Laplacian on bounded
domains''. Journal of Spectral Theory.
2018 DOI 10.4171/JST/200 22pp.
-
``Partial differential equations,
spectral theory, and mathematical
physics - the Ari Laptev anniversary
volume.'' Edited by Pavel Exner, Rupert
L. Frank, Fritz Gesztesy, Helge Holden
and Timo Weidl. EMS Series of Congress
Reports. EMS Press, Berlin, 2021, xii+481 pp. ISBN: 978-3-98547-007-5
-
Frank, R., Laptev, A., Weidl,
T. ``Schrödinger Operators:
Eigenvalues and Lieb - Thirring
Inequalities''. (Cambridge Studies in
Advanced Mathematics 200). Cambridge:
Cambridge University Press. to appear
in November 2022. Online ISBN: 9781009218436
- Rupert L. Frank, Ari Laptev, Timo Weidl ``An improved one-dimensional Hardy inequality''. arXiv:2204.00877 (2022)
|

