Geometric Hermite Interpolation
A smooth planar curve with non-vanishing curvature
can be approximated by cubic splines with order 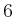 ,
rather than order
,
rather than order 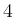 as expected in view of Taylor's
theorem.
The figure illustrates how a spline segment
as expected in view of Taylor's
theorem.
The figure illustrates how a spline segment 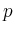 can
be constructed with the aid of the Bézier
representation
can
be constructed with the aid of the Bézier
representation
by interpolating position, tangent direction,
and curvature at the endpoints.
It is conjectured that spline curves of degree 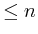 approximate smooth curves in
approximate smooth curves in
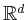 with order
with order
as the maximal length 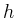 of the spline segments tends
to zero.
of the spline segments tends
to zero.
 with C. de Boor and M. Sabin, CAGD 4 (1987), 269-278.
with C. de Boor and M. Sabin, CAGD 4 (1987), 269-278.
![$\displaystyle t\mapsto p(t) =
\sum_{k=0}^3 c_k\,\binom{3}{k}(1-t)^{3-k}t^k,\quad
t\in[0,1]
\,,
$](img4.png)
![$\displaystyle t\mapsto p(t) =
\sum_{k=0}^3 c_k\,\binom{3}{k}(1-t)^{3-k}t^k,\quad
t\in[0,1]
\,,
$](img4.png)
![\includegraphics[width=10cm]{HermiteFig.eps}](img5.png)
![]() approximate smooth curves in
approximate smooth curves in
![]() with order
with order
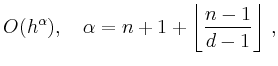
![]() with C. de Boor and M. Sabin, CAGD 4 (1987), 269-278.
with C. de Boor and M. Sabin, CAGD 4 (1987), 269-278.