Multigrid Convergence
Let 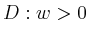 be a bounded domain in
be a bounded domain in
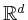 ,
described by a smooth positive weight function with
,
described by a smooth positive weight function with
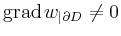 and denote
by
and denote
by 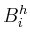 ,
, 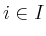 ,
the weighted extended b-spline basis for
,
the weighted extended b-spline basis for 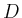 .
Then, the Ritz-Galerkin system
.
Then, the Ritz-Galerkin system
for the finite element approximation
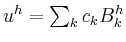 of Poisson's equation
can be solved by a multigrid
iteration based on b-spline subdivision.
of Poisson's equation
can be solved by a multigrid
iteration based on b-spline subdivision.
The convergence rate of the 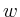 -cycle is independent of
-cycle is independent of
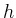 if sufficiently many smoothing steps are used.
if sufficiently many smoothing steps are used.
 with U. Reif and J. Wipper,
Numerische Mathematik 91 No. 2 (2002), 237-256.
with U. Reif and J. Wipper,
Numerische Mathematik 91 No. 2 (2002), 237-256.
 Finite Element Methods with B-Splines, SIAM, 2003.
Finite Element Methods with B-Splines, SIAM, 2003.
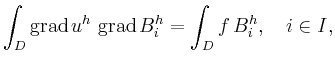
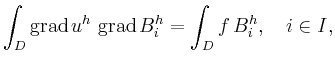

![]() -cycle is independent of
-cycle is independent of
![]() if sufficiently many smoothing steps are used.
if sufficiently many smoothing steps are used.
![]() with U. Reif and J. Wipper,
Numerische Mathematik 91 No. 2 (2002), 237-256.
with U. Reif and J. Wipper,
Numerische Mathematik 91 No. 2 (2002), 237-256.
![]() Finite Element Methods with B-Splines, SIAM, 2003.
Finite Element Methods with B-Splines, SIAM, 2003.