




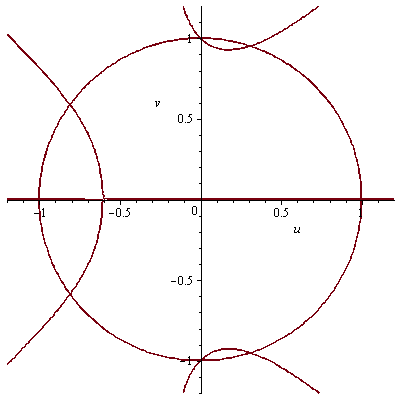





Erstellt von Daniel Banov, Michael Bitzer und Sara Catarinella.
Sei Phi_n das n-te Kreisteilungspolynom.
Für p prim und betragsgroße z ist Phi_{3p}(z) etwa gleich z^(2(p-1)).
Für betragskleine z ist Phi_{3p}(z) = ((z^(3p) - 1)(z - 1))/((z^p - 1)(z^3 - 1)) = Phi_3(z^p)/Phi_3(z) etwa gleich 1/Phi_3(z), dessen Realteil genau dann verschwindet, wenn Re(\overline{Phi_3(z)}) verschwindet, i.e. wenn Re(Phi_3(z)) verschwindet. Analog für den Imaginärteil.
Genauso für 5, 7 oder 11 anstelle von 3.
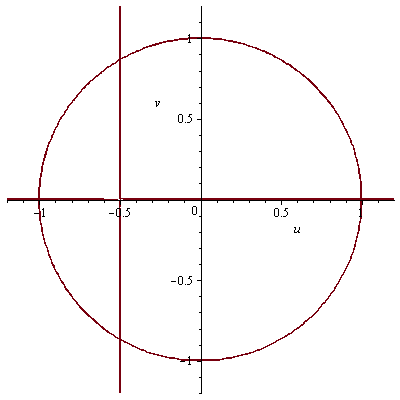
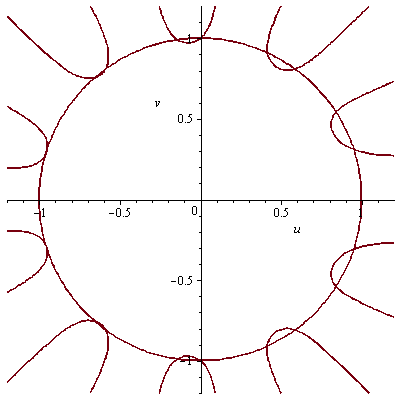
Nullstellen von Re(Phi_{3p}(z)) mit p prim laufend.
|
Nullstellen von Re(Phi_3(z)) (samt Kreis).
|
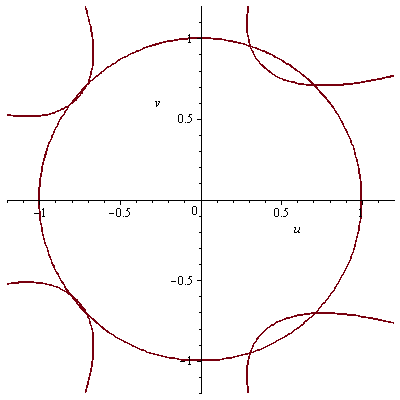
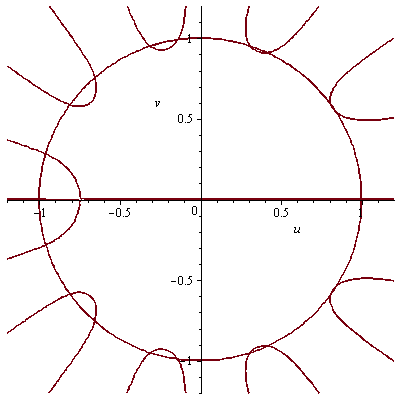
Nullstellen von Im(Phi_{3p}(z)) mit p prim laufend.
|
Nullstellen von Im(Phi_3(z)) (samt Kreis).
|
Nullstellen von Re(Phi_{5p}(z)) mit p prim laufend.
|
Nullstellen von Re(Phi_5(z)) (samt Kreis).
|
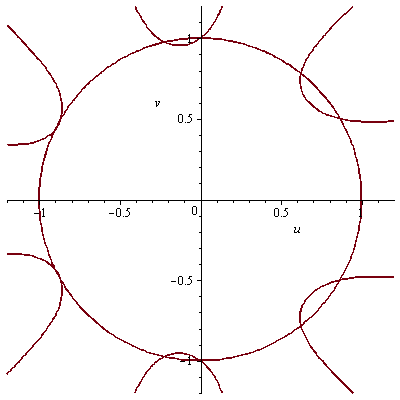
Nullstellen von Im(Phi_{5p}(z)) mit p prim laufend.
|
Nullstellen von Im(Phi_5(z)) (samt Kreis).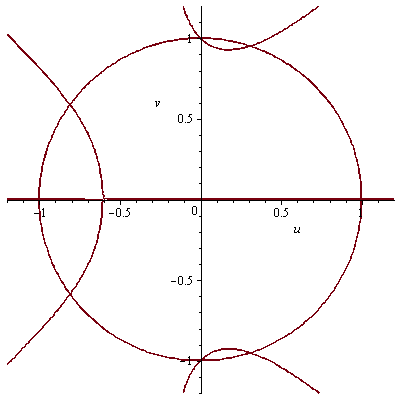
|
Nullstellen von Re(Phi_{7p}(z)) mit p prim laufend.
|
Nullstellen von Re(Phi_7(z)) (samt Kreis).
|
Nullstellen von Im(Phi_{7p}(z)) mit p prim laufend.
|
Nullstellen von Im(Phi_7(z)) (samt Kreis).
|
Nullstellen von Re(Phi_{11p}(z)) mit p prim laufend.
|
Nullstellen von Re(Phi_{11}(z)) (samt Kreis).
|
Nullstellen von Im(Phi_{11p}(z)) mit p prim laufend.
|
Nullstellen von Im(Phi_{11}(z)) (samt Kreis).
|