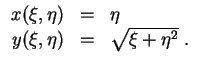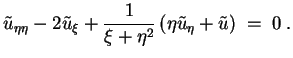Es ist
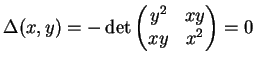 für alle
für alle
 , die Gleichung also auf
, die Gleichung also auf
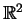 parabolisch.
Die charakteristische Gleichung
parabolisch.
Die charakteristische Gleichung
wird durch
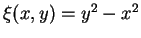 gelöst, wobei
gelöst, wobei
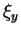 in der Tat nicht identisch verschwindet. Mit
in der Tat nicht identisch verschwindet. Mit
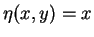 erhalten wir für
erhalten wir für
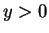 die Umkehrtransformation
Damit erhält man nach Division durch den Koeffizienten
die Umkehrtransformation
Damit erhält man nach Division durch den Koeffizienten
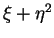 von
von
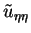
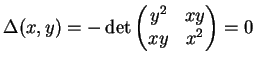 für alle
für alle
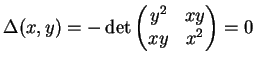 für alle
für alle
![]() , die Gleichung also auf
, die Gleichung also auf
![]() parabolisch.
Die charakteristische Gleichung
parabolisch.
Die charakteristische Gleichung