Es ist
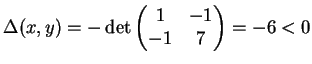 für alle
für alle
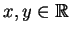 , die Gleichung also auf
, die Gleichung also auf
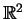 elliptisch.
Als komplexe Lösung von
elliptisch.
Als komplexe Lösung von
ist
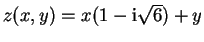 zu sehen. Mit der Substitution
zu sehen. Mit der Substitution
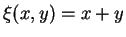 und
und
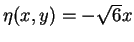 erhalten wir
mit der allgemeinen Lösung
mit beliebigen (zweimal differenzierbaren) Funktionen
erhalten wir
mit der allgemeinen Lösung
mit beliebigen (zweimal differenzierbaren) Funktionen
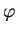 und
und
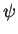 . Für reellwertige Lösungen ist davon der Real- oder der Imaginärteil zu nehmen.
. Für reellwertige Lösungen ist davon der Real- oder der Imaginärteil zu nehmen.
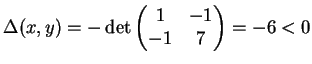 für alle
für alle
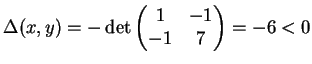 für alle
für alle
![]() , die Gleichung also auf
, die Gleichung also auf
![]() elliptisch.
Als komplexe Lösung von
elliptisch.
Als komplexe Lösung von