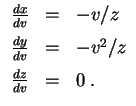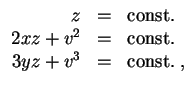Setzt man
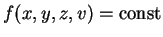 mit
mit
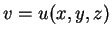 an, so ist die lineare Gleichung
an, so ist die lineare Gleichung
in den Variablen
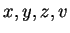 zu lösen.
zu lösen.
Aus dem Gleichungssystem für die Charakteristiken
erhält man wegen
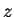 konstant in
konstant in
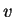 die Charakteristiken implizit beschrieben durch
und also die unabhängigen Lösungen
die Charakteristiken implizit beschrieben durch
und also die unabhängigen Lösungen
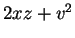 ,
,
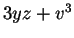 und
und
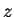 .
.
Die Lösung der ursprünglichen quasi-linearen Gleichung ist dann implizit gegeben durch
mit
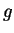 beliebig, aber nicht unabhängig von den ersten beiden Variablen, und auch
dann so, daß
beliebig, aber nicht unabhängig von den ersten beiden Variablen, und auch
dann so, daß
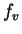 nicht identisch verschwindet.
nicht identisch verschwindet.
![]() mit
mit
![]() an, so ist die lineare Gleichung
an, so ist die lineare Gleichung