Sei die Verkehrsdichte auf einer Straße durch
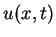 gegeben, d.h.
gegeben, d.h.
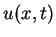 ist die Zahl der Autos an der Stelle
ist die Zahl der Autos an der Stelle
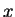 zum Zeitpunkt
zum Zeitpunkt
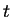 zwischen
zwischen
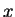 und
und
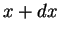 ,
geteilt durch
,
geteilt durch
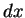 .
.
Sei der Verkehrsfluß durch
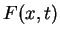 beschrieben. Der Wert
beschrieben. Der Wert
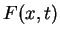 ist hierbei die Zahl der Autos, die die Stelle
ist hierbei die Zahl der Autos, die die Stelle
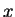 im Zeitraum von
im Zeitraum von
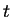 bis
bis
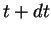 in positiver Richtung passieren.
in positiver Richtung passieren.
Betrachten wir das Streckenelement
![$ \mbox{$[x,x+dx]$}$](img8.gif) zum Zeitpunkt
zum Zeitpunkt
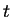 . Fluß und Dichte hängen über
. Fluß und Dichte hängen über
zusammen, da die Änderung der Verkehrsdichte der Zahl der in das Streckenelement bei
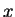 einfahrenden Autos, minus der bei
einfahrenden Autos, minus der bei
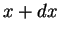 ausfahrenden Autos gegeben ist.
Also
ausfahrenden Autos gegeben ist.
Also
- (i)
- Sei der Verkehrsfluß
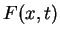 nur von
nur von
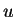 abhängig - die Geschwindigkeit eines Autos ist durch den Abstand zum Vordermann bestimmt.
Wir setzen also
abhängig - die Geschwindigkeit eines Autos ist durch den Abstand zum Vordermann bestimmt.
Wir setzen also
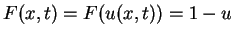 an. D.h. ist die Verkehrsdichte Null, so fahren alle Autos mit Geschwindigkeit
an. D.h. ist die Verkehrsdichte Null, so fahren alle Autos mit Geschwindigkeit
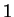 , ist die Verkehrsdichte auf
, ist die Verkehrsdichte auf
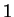 angeschwollen,
so kommt der Verkehr zum Erliegen. Ist die Verkehrsdichte
angeschwollen,
so kommt der Verkehr zum Erliegen. Ist die Verkehrsdichte
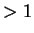 , so kommt es zu Auffahrunfällen.
, so kommt es zu Auffahrunfällen.
- (ii)
- Sei nun der Verkehrfluß noch von der sich den Orten
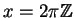 befindlichen Polizeistationen abhängig - je näher an
befindlichen Polizeistationen abhängig - je näher an
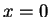 , desto mehr wird auf den zu geringen
Abstand zum Vordermann mit Geschwindigkeitsreduktion reagiert. Sei demgemäß
, desto mehr wird auf den zu geringen
Abstand zum Vordermann mit Geschwindigkeitsreduktion reagiert. Sei demgemäß
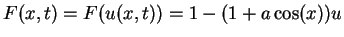 mit
mit
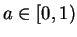 .
.
Gib die allgemeine Lösung der Differentialgleichung in den Fällen (i, ii) an.
Sei nun als Randbedingung
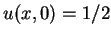 vorausgesetzt. Gib die Funktion
vorausgesetzt. Gib die Funktion
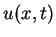 in beiden Fällen an.
in beiden Fällen an.
![]() gegeben, d.h.
gegeben, d.h.
![]() ist die Zahl der Autos an der Stelle
ist die Zahl der Autos an der Stelle
![]() zum Zeitpunkt
zum Zeitpunkt
![]() zwischen
zwischen
![]() und
und
![]() ,
geteilt durch
,
geteilt durch
![]() .
.
![]() beschrieben. Der Wert
beschrieben. Der Wert
![]() ist hierbei die Zahl der Autos, die die Stelle
ist hierbei die Zahl der Autos, die die Stelle
![]() im Zeitraum von
im Zeitraum von
![]() bis
bis
![]() in positiver Richtung passieren.
in positiver Richtung passieren.
![]() zum Zeitpunkt
zum Zeitpunkt
![]() . Fluß und Dichte hängen über
. Fluß und Dichte hängen über
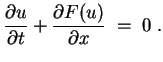
![]() vorausgesetzt. Gib die Funktion
vorausgesetzt. Gib die Funktion
![]() in beiden Fällen an.
in beiden Fällen an.