Lösung.

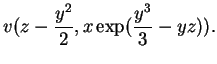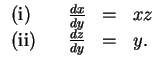
Die Phasen-Differentialgleichungen sind

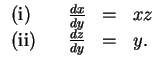
$ \mbox{$\displaystyle \begin{array}{lllll} \text{(i)} && \frac{dx}{dy} &=& xz\\ \text{(ii)} && \frac{dz}{dy} &=& y. \end{array}$}$
Aus (ii) folgt $ \mbox{$dz = y\, dy$}$ und damit $ \mbox{$z = \frac{y^2}{2} + c_1$}$ mit einer Konstanten $ \mbox{$c_1\in\mathbb{R}$}$.

Aus (i) folgt mit (ii) zunächst 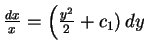$ \mbox{$\frac{dx}{x} = \left(\frac{y^2}{2}+c_1)\,dy$}$ und damit $ \mbox{$\log x = \frac{y^3}{6} + yc_1 + c_2$}$ mit einer Konstanten $ \mbox{$c_2\in\mathbb{R}$}$; dies kann noch zu $ \mbox{$\exp(c_2) = x\exp(\frac{-y^3}{6} - yc_1) = x\exp(\frac{y^3}{3}-yz)$}$ vereinfacht werden.

Die Charakteristiken der DGL sind also

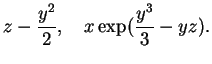
$ \mbox{$\displaystyle z-\frac{y^2}{2},\quad x\exp(\frac{y^3}{3}-yz). $}$

Die allgemeine Lösung der Rumpf-DGL ist für eine beliebige Funktion $ \mbox{$v:\mathbb{R}^2\to\mathbb{R}$}$ entlang der Charakteristiken dann gegeben durch

$ \mbox{$\displaystyle v(z-\frac{y^2}{2}, x\exp(\frac{y^3}{3}-yz)). $}$