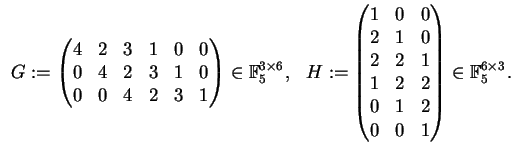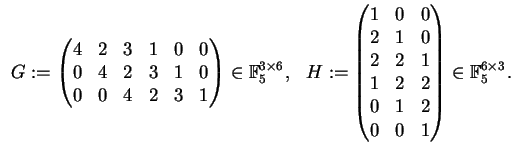- Polynomdivision von
 durch
durch
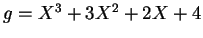 ergibt
ergibt
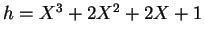 .
.
- Eine Erzeuger- und eine Prüfmatrix sind
- Das Polynom
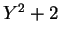 vom Grade
vom Grade
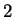 hat keine Nullstellen in
hat keine Nullstellen in
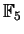 .
Wäre es reduzibel, so könnte man einen Linearfaktor abspalten welcher eine
Nullstelle liefern würde. Das Polynom ist also irreduzibel.
.
Wäre es reduzibel, so könnte man einen Linearfaktor abspalten welcher eine
Nullstelle liefern würde. Das Polynom ist also irreduzibel.
- Wir erhalten
- Aus
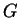 liest man ab, daß
liest man ab, daß
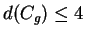 gelten muß.
Es ist
gelten muß.
Es ist
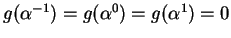 . Nach der bekannten Abschätzung für
die Minimaldistanz eines zyklischen Codes folgt
. Nach der bekannten Abschätzung für
die Minimaldistanz eines zyklischen Codes folgt
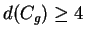 . Also ist
. Also ist
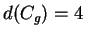 .
.
- Es ist
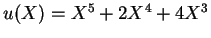 . Polynomdivision durch
. Polynomdivision durch
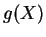 ergibt einen
Rest
ergibt einen
Rest
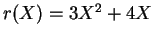 . Man verwendet als Codewort dann
. Man verwendet als Codewort dann
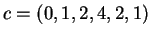 .
.