Lösung.

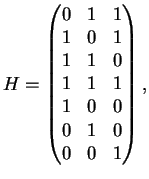
Mit Hilfe der Prüfmatrix

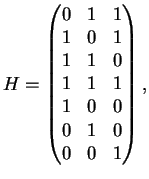
$ \mbox{$\displaystyle H=\begin{pmatrix}0&1&1\\ 1&0&1\\ 1&1&0\\ 1&1&1\\ 1&0&0\\ 0&1&0\\ 0&0&1\end{pmatrix}, $}$
die zeigt, daß es sich um einen Hamming Code handelt, folgt durch Rechnung folgende Tabelle.
empfangenes Wort Syndrom decodiertes Wort Buchstabe
$ \mbox{$(0, 0, 0, 0, 0, 1, 1)$}$ $ \mbox{$(0,1,1)$}$ $ \mbox{$(1, 0, 0, 0, 0, 1, 1)$}$ H
$ \mbox{$(1, 1, 0, 1, 0, 0, 0)$}$ $ \mbox{$(0,0,1)$}$ $ \mbox{$(1, 1, 0, 1, 0, 0, 1)$}$ M
$ \mbox{$(0, 0, 1, 0, 0, 0, 0)$}$ $ \mbox{$(1,1,0)$}$ $ \mbox{$(0, 0, 0, 0, 0, 0, 0)$}$ [ ]
$ \mbox{$(1, 1, 1, 1, 1, 1, 1)$}$ $ \mbox{$(0,0,0)$}$ $ \mbox{$(1, 1, 1, 1, 1, 1, 1)$}$ O
$ \mbox{$(1, 1, 1, 1, 0, 0, 0)$}$ $ \mbox{$(1,1,1)$}$ $ \mbox{$(1, 1, 1, 0, 0, 0, 0)$}$ N
$ \mbox{$(1, 1, 0, 0, 1, 1, 0)$}$ $ \mbox{$(0,0,0)$}$ $ \mbox{$(1, 1, 0, 0, 1, 1, 0)$}$ L
$ \mbox{$(1, 0, 0, 1, 1, 0, 0)$}$ $ \mbox{$(0,0,0)$}$ $ \mbox{$(1, 0, 0, 1, 1, 0, 0)$}$ I
$ \mbox{$(1, 1, 0, 1, 0, 0, 0)$}$ $ \mbox{$(0,0,1)$}$ $ \mbox{$(1, 1, 0, 1, 0, 0, 1)$}$ M
$ \mbox{$(0, 1, 0, 1, 1, 1, 1)$}$ $ \mbox{$(1,0,1)$}$ $ \mbox{$(0, 0, 0, 1, 1, 1, 1)$}$ A

Es ergibt sich ,,HM ONLIMA``. Beim vorletzten Buchstaben sind bei der Übertragung zwei Bits umgekippt; der MDD eines binären Hamming Codes kann dies jedoch nicht erkennen und hat stattdessen eine Korrektur zum ,,falschen`` Codewort durchgeführt. Beim letzen Buchstaben haben zwei falsch übertragene Prüfbits die ursprünglich richtigen ersten vier Informationsbits verfälscht.