Lösung

Umsortieren der Spalten der Erzeugermatrix von $ \mbox{$G$}$ ergibt die Erzeugermatrix $ \mbox{$G'$}$ eines äquivalenten Codes $ \mbox{$C'$}$,

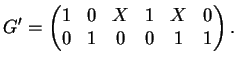
$ \mbox{$\displaystyle G'=\begin{pmatrix}1&0&X&1&X&0\\ 0&1&0&0&1&1\end{pmatrix}. $}$

Um die Minimaldistanz $ \mbox{$d(C)=d(C')$}$ zu bestimmen, beachte man, daß für jede Linearkombination $ \mbox{$x=a (1,0,X,1,X,0) + b (0,1,0,0,1,1)$}$ mit $ \mbox{$a\neq 0$}$ oder aber $ \mbox{$a=0$}$ und $ \mbox{$b\neq 0$}$ gilt, daß $ \mbox{$d(x,0)\geq 3$}$ ist. Damit folgt $ \mbox{$d(C)=3$}$.

Die Informationsrate ist $ \mbox{$r(C) = \frac{1}{3}$}$. Es handelt sich um einen $ \mbox{$[6,2,3]$}$-Code.

Die Prüfmatrix zu $ \mbox{$G'$}$ ist

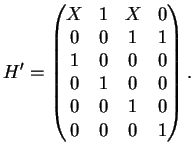
$ \mbox{$\displaystyle H'=\begin{pmatrix}X&1&X&0\\ 0&0&1&1\\ 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\end{pmatrix}. $}$
Zu jedem Syndrom $ \mbox{$s\in\{$}$ $ \mbox{$0$}$, $ \mbox{$(1,0,0,0)$}$, $ \mbox{$(0,1,0,0)$}$, $ \mbox{$(1,1,1,1)$}$, $ \mbox{$(X+1,X,1,0)$}$, $ \mbox{$(X+1,X+1,1,0)$}$ $ \mbox{$\}$}$ ist ein minimaler Vertreter, d.h. ein $ \mbox{$a'\in\mathbb{F}_4^6$}$ mit $ \mbox{$a'H = s$}$ und mit minimaler Distanz zu $ \mbox{$0$}$ anzugeben. Die folgende Tabelle enstand durch Überprüfen aller jeweils $ \mbox{$4^2$}$ Fälle unter Verwendung von $ \mbox{$\{x\in\mathbb{F}_4^6 : xH = s\} = x_0 + \{x\in\mathbb{F}_4^6 : xH=0\}$}$ für jeweils ein $ \mbox{$x_0\in\mathbb{F}_4^6$}$ mit $ \mbox{$x_0H=s$}$.

Syndrom ein minimaler Vertreter
$ \mbox{$(0,0,0,0)$}$ $ \mbox{$(0,0,0,0,0,0)$}$
$ \mbox{$(1,0,0,0)$}$ $ \mbox{$(0,0,1,0,0,0)$}$
$ \mbox{$(0,1,0,0)$}$ $ \mbox{$(0,0,0,1,0,0)$}$
$ \mbox{$(1,1,1,1)$}$ $ \mbox{$(0,1,1,1,0,0)$}$
$ \mbox{$(X+1,X,1,0)$}$ $ \mbox{$(X,0,0,0,X,0)$}$
$ \mbox{$(X+1,X+1,1,0)$}$ $ \mbox{$(X+1,0,X,0,0,0)$}$

Das Codewort $ \mbox{$c=(1,0,X,1,X,0)$}$ werde durch einen Übertragungsfehler $ \mbox{$e=(X+1,0,X,0,0,0)$}$ als $ \mbox{$(c+e)=(X,0,0,1,X,0)$}$ empfangen. Das zugehörige Syndrom ist

$ \mbox{$\displaystyle (c+e)H = (X+1,X+1,1,0) $}$
und nach obiger Tabelle gilt für unseren zugehörigen MDD
$ \mbox{$\displaystyle f(c+e) = (X,0,0,1,X,0) - (X+1,0,X,0,0,0) = (1, 0, X, 1, X, 0) = c. $}$
Die Decodierung hat (bei dieser Wahl von $ \mbox{$c$}$ und $ \mbox{$e$}$) auch bei zwei Übertragunsfehlern funktioniert, obwohl die Minimaldistanz $ \mbox{$d(C)=3$}$ ist.