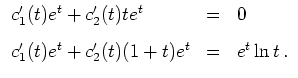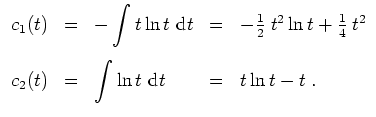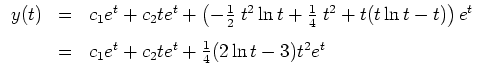Lösung.

Das charakteristische Polynom der zugehörigen homogenen Differentialgleichung ist

$ \mbox{$\displaystyle \chi(X) \;=\; X^2-2X+1=(X-1)^2\; . $}$
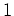Also ist $ \mbox{$1$}$ eine doppelte Nullstelle, und wir erhalten eine Basis
$ \mbox{$\displaystyle (\; e^t,\; te^t \; ) $}$
des Lösungsraumes.

Die rechte Seite der Differentialgleichung hat keine einfache Gestalt, also verwenden wir die Methode der Variation der Konstanten. Für eine partikuläre Lösung setzen wir demgemäß

$ \mbox{$\displaystyle y_\text{p}(t) \;=\; c_1(t)e^t + c_2(t)te^t $}$
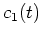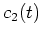mit noch zu bestimmenden Funktionen $ \mbox{$c_1(t)$}$ und $ \mbox{$c_2(t)$}$ an und erhalten die Bedingungen
$ \mbox{$\displaystyle \begin{array}{lcl} c_1'(t)e^t+c_2'(t)te^t &=& 0\vspace{3mm}\\ c_1'(t)e^t+c_2'(t)(1+t)e^t &=& e^t\ln t\,. \end{array}$}$
Eine Betrachtung der Differenz gibt 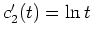$ \mbox{$c_2'(t)=\ln t\,$}$ , so daß 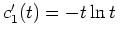$ \mbox{$c_1'(t)=-t\ln t\,$}$ . Somit werden
$ \mbox{$\displaystyle \begin{array}{rclcl} c_1(t) &=& -\displaystyle\int t\ln ... ...) &=& \displaystyle\int\ln t\ \text{d}t & = & t\ln t - t\; . \\ \end{array}$}$
Die allgemeine Lösung setzt sich nun zusammen zu
$ \mbox{$\displaystyle \begin{array}{rcl} y(t)&=& c_1e^t+c_2te^t+\left(-\frac{... ...^t\vspace{3mm}\\ &=& c_1e^t+c_2te^t+\frac{1}{4}(2\ln t-3)t^2e^t \end{array}$}$
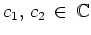mit $ \mbox{$c_1,\, c_2 \,\in\, \mathbb{C}$}$ .