Lösung.

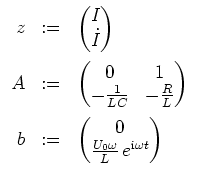
Wir wollen den in der Wiederholung mit III bezeichneten Lösungsweg verwenden.

Wir setzen hierzu

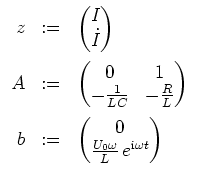
$ \mbox{$\displaystyle \begin{array}{rcl} z & := & \begin{pmatrix}I \\ \dot I\... ...\\ \frac{U_0\omega}{L}\,e^{\mathrm{i}\omega t}\end{pmatrix} \\ \end{array}$}$
und lösen $ \mbox{$\dot z = Az + b$}$ . Schreibe $ \mbox{$c := -\frac{1}{LC}$}$ , $ \mbox{$r := -\frac{R}{L}$}$ und $ \mbox{$u := \frac{U_0\omega}{L}$}$ . Am Ende müssen wir dann wieder von $ \mbox{$e^{\mathrm{i}\omega t}$}$ zu $ \mbox{$\cos(\omega t)$}$ übergehen.

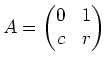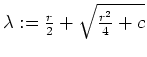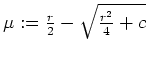Wir wollen $ \mbox{$\exp(tA)$}$ berechnen. Da die Matrix $ \mbox{$A = \begin{pmatrix}0&1\\ c&r\end{pmatrix}$}$ Parameter enthält, gehen wir näher auf diese Berechnung ein. Ihre Eigenwerte sind $ \mbox{$\lambda := \frac{r}{2} + \sqrt{\frac{r^2}{4} + c}$}$ und $ \mbox{$\mu := \frac{r}{2} - \sqrt{\frac{r^2}{4} + c}$}$ , und nach Voraussetzung an $ \mbox{$R$}$ verschieden und beide reell.

Die Jordanform ergibt sich zu

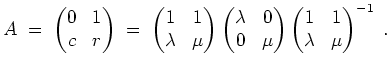
$ \mbox{$\displaystyle A \;=\; \begin{pmatrix}0&1\\ c&r\end{pmatrix} \;=\; \be... ... 0&\mu\end{pmatrix} \begin{pmatrix}1&1\\ \lambda&\mu\end{pmatrix}^{-1}\; . $}$
Somit ist
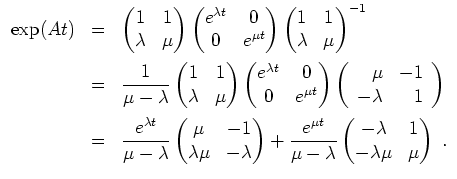
$ \mbox{$\displaystyle \begin{array}{rcl} \exp(At) & = & \begin{pmatrix}1&1\\ ... ...egin{pmatrix}-\lambda&1\\ -\lambda\mu&\mu\end{pmatrix} \; . \\ \end{array}$}$

Für die Variation der Konstanten beachten wir zunächst, daß wir nach Ersetzen von $ \mbox{$t$}$ durch $ \mbox{$-t$}$

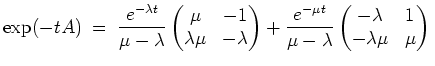
$ \mbox{$\displaystyle \exp(-tA) \;=\; \frac{e^{-\lambda t}}{\mu - \lambda} \be... ...\mu - \lambda} \begin{pmatrix}-\lambda&1\\ -\lambda\mu&\mu\end{pmatrix} \\ $}$
erhalten. Nun wird, für beliebig wählbare Konstanten $ \mbox{$\alpha,\,\beta\,\in\,\mathbb{C}$}$ ,
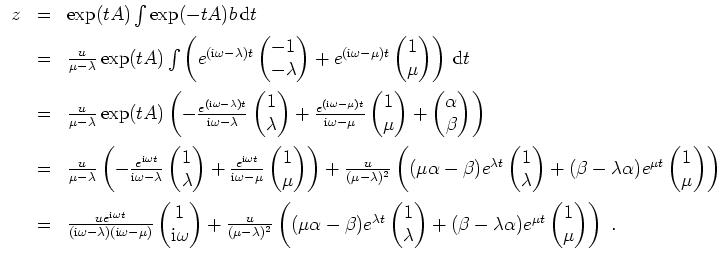
$ \mbox{$\displaystyle \begin{array}{rcl} z & = & \exp(tA)\int\exp(-tA)b\,\tex... ...ha)e^{\mu t}\begin{pmatrix}1 \\ \mu\end{pmatrix}\right) \; .\\ \end{array}$}$
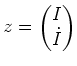Reskalieren der Konstanten $ \mbox{$\alpha$}$ und $ \mbox{$\beta$}$ zu Konstanten $ \mbox{$I_1,\, I_2\,\in\,\mathbb{C}$}$ und Betrachten des ersten Eintrags $ \mbox{$I$}$ von $ \mbox{$z = \begin{pmatrix}I \\ \dot I\end{pmatrix}$}$ liefert die allgemeine Lösung
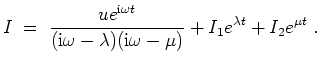
$ \mbox{$\displaystyle I \;=\; \frac{u e^{\mathrm{i}\omega t}}{(\mathrm{i}\omega - \lambda)(\mathrm{i}\omega - \mu)} + I_1 e^{\lambda t} + I_2 e^{\mu t} \; . $}$
Da wir anstelle von $ \mbox{$\cos(\omega t)$}$ von $ \mbox{$e^{\mathrm{i}\omega t}$}$ ausgegangen waren, müssen wir im ersten Summanden noch den Realteil bilden, was
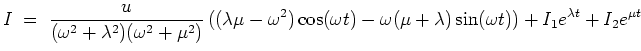
$ \mbox{$\displaystyle I \;=\; \frac{u}{(\omega^2 + \lambda^2)(\omega^2 + \mu^2... ... - \omega(\mu + \lambda)\sin(\omega t)) + I_1 e^{\lambda t} + I_2 e^{\mu t} $}$
liefert. Teilweises Rückeinsetzen der ursprünglichen Größen
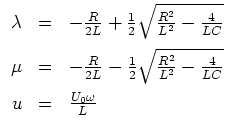
$ \mbox{$\displaystyle \begin{array}{rcl} \lambda & = & -\frac{R}{2L} + \frac{1... ... \frac{4}{LC}}\vspace*{2mm} \\ u & = & \frac{U_0\omega}{L} \\ \end{array}$}$
bringt die allgemeine Lösung auf die Form
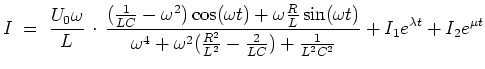
$ \mbox{$\displaystyle I \;=\; \dfrac{U_0\omega}{L}\,\cdot\,\dfrac{(\frac{1}{LC... ...2} - \frac{2}{LC}) + \frac{1}{L^2 C^2}} + I_1 e^{\lambda t} + I_2 e^{\mu t} $}$
für $ \mbox{$I_1,\, I_2\,\in\,\mathbb{C}$}$ beliebig gewählt. In der Praxis sind hier, da $ \mbox{$\lambda$}$ und $ \mbox{$\mu$}$ reell sind, auch die Stromstärken $ \mbox{$I_1$}$ und $ \mbox{$I_2$}$ reell.

Skizze für $ \mbox{$U_0 = 1$}$ , $ \mbox{$L = 10$}$ , $ \mbox{$\omega = 1$}$ , $ \mbox{$C = 5$}$ , $ \mbox{$R \in \{50,10,3\}$}$ (von oben nach unten), $ \mbox{$I_1 = 0{,}5$}$ und $ \mbox{$I_2 = -2$}$ .

\includegraphics[width = 8cm]{RCL.eps}

Interpretation. Nach Abklingen des homogenen Bestandteils $ \mbox{$I_1 e^{\lambda t} + I_2 e^{\mu t}$}$ verbleibt für große $ \mbox{$t$}$ eine Schwingung mit Frequenz $ \mbox{$\omega$}$ gleich der Erregerfrequenz. Die Phasenverschiebung im Vergleich zur Erregerspannung, sowie die Amplitude können der oben hergeleiteten Formel entnommen werden.