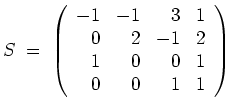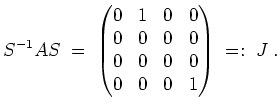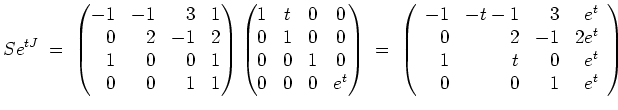Das charakteristische Polynom von
 ist
ist
also hat
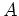 die Eigenwerte
die Eigenwerte
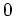 und
und
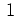 . Wir berechnen nun die Jordanform von
. Wir berechnen nun die Jordanform von
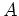 mit einer Transformationsmatrix
mit einer Transformationsmatrix
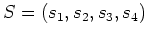 .
.
Für den Eigenwert
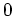 setzen wir
setzen wir
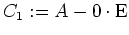 und berechnen
und berechnen
Außerdem ist
und wir ergänzen
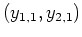 mit
mit
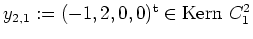 zu einer Basis
zu einer Basis
 von
von
 , die auch Basis des Hauptraums
, die auch Basis des Hauptraums
 ist. Nun ergänzen wir
ist. Nun ergänzen wir
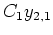 mit
mit
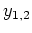 zu einer Basis
zu einer Basis
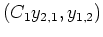 von
von
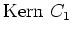 und setzen
und setzen
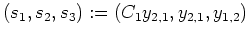 .
.
Für den Eigenwert
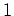 setzen wir
setzen wir
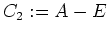 und erhalten
und erhalten
Dies ist eine Basis des Hauptraums
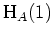 , also wählen wir
, also wählen wir
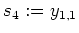 .
.
Mit
gilt also nun
Somit erhalten wir
eine Fundamentalmatrix, so daß die allgemeine Lösung der Differentialgleichung
mit einem Vektor
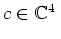 lautet.
lautet.
![]() ist
ist
![]() setzen wir
setzen wir
![]() und berechnen
und berechnen
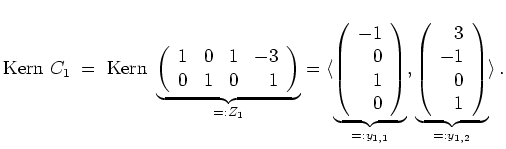
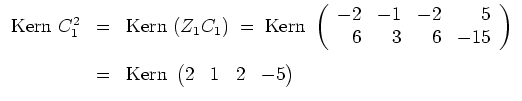
![]() setzen wir
setzen wir
![]() und erhalten
und erhalten