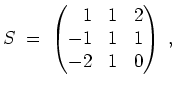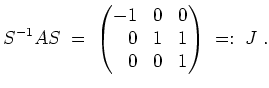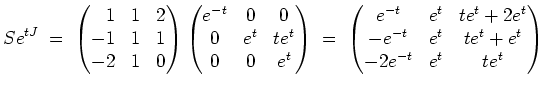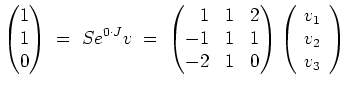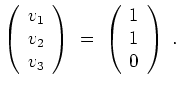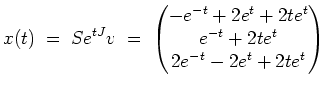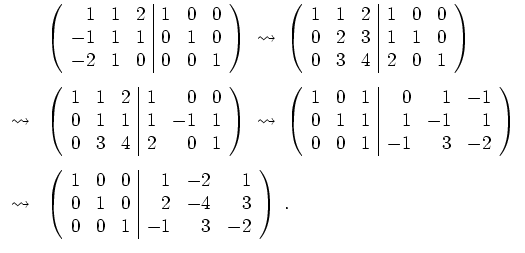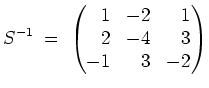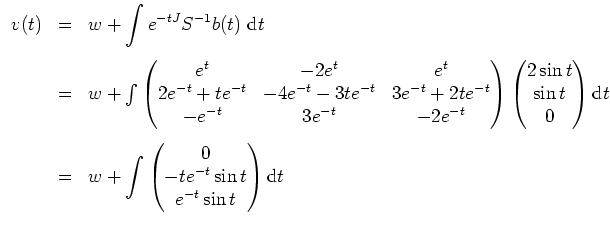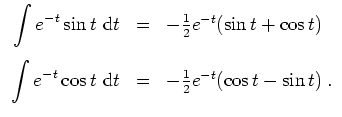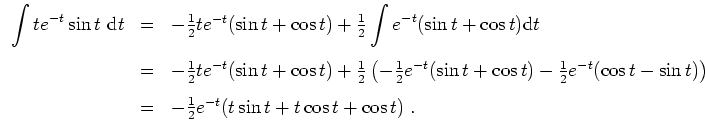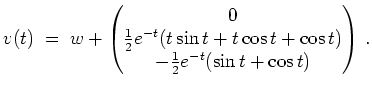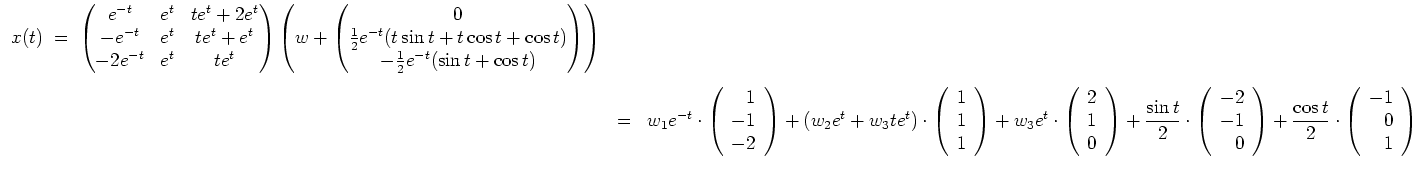Zunächst berechnen wir das charakteristische Polynom
Also hat
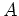 die Eigenwerte
die Eigenwerte
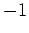 und
und
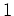 . Wir berechnen nun die Jordanform von
. Wir berechnen nun die Jordanform von
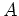 mit einer Transformationsmatrix
mit einer Transformationsmatrix
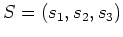 .
Für den Eigenwert
.
Für den Eigenwert
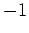 setzen wir
setzen wir
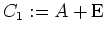 und erhalten sofort
Dies ist eine Basis des Hauptraums
und erhalten sofort
Dies ist eine Basis des Hauptraums
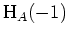 , also wählen wir
, also wählen wir
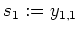 .
.
Für den Eigenwert
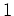 setzen wir
setzen wir
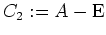 und berechnen
sowie
woraus wir eine Basis
und berechnen
sowie
woraus wir eine Basis
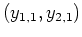 des Hauptraums
des Hauptraums
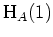 erhalten.
erhalten.
Wir ersetzen nun im nächsten Schritt diese Basis durch die einzige hier erforderliche Kette
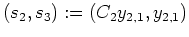 , welche ebenfalls eine Basis des Hauptraums
, welche ebenfalls eine Basis des Hauptraums
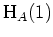 darstellt.
(Daß
darstellt.
(Daß
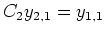 ist, darf als Zufall angesehen werden.) Insgesamt erhalten wir
ist, darf als Zufall angesehen werden.) Insgesamt erhalten wir
und es ist
Dann ist also
eine Fundamentalmatrix, so daß die allgemeine Lösung der Differentialgleichung die Gestalt
hat, mit einem Vektor
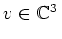 .
.
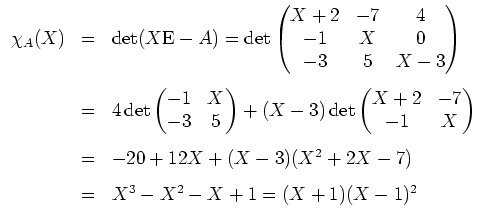
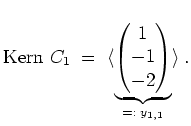
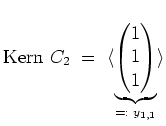
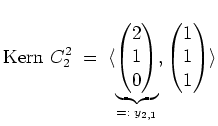
![]() , welche ebenfalls eine Basis des Hauptraums
, welche ebenfalls eine Basis des Hauptraums
![]() darstellt.
(Daß
darstellt.
(Daß
![]() ist, darf als Zufall angesehen werden.) Insgesamt erhalten wir
ist, darf als Zufall angesehen werden.) Insgesamt erhalten wir