
Die gegebene Diagonalmatrix

ist in Jordanform. Damit ist also ein Fundamentalmatrix der Differentialgleichung gegeben durch
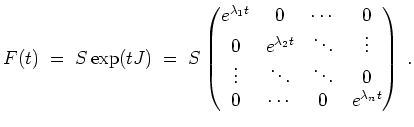
Diesen Umstand kann man sich alternativ auch leicht wie folgt erklären.
Substituiert man
![]() , bzw.
, bzw.
![]() , so führt das gegebene System
, so führt das gegebene System
![]() auf das System
auf das System
![]() , d.h. auf das System
, d.h. auf das System
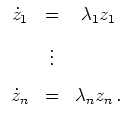
Zu diesem System ist eine Fundamentalmatrix leicht auffindbar, nämlich

Die Resubstitution
![]() führt schließlich auf die gewünschte Behauptung.
führt schließlich auf die gewünschte Behauptung.