Die Matrixexponentialfunktion.

Definition.

Es sei $ \mbox{$n\ge 1$}$ und $ \mbox{$A\in\mathbb{C}^{n\times n}$}$ . Wir definieren

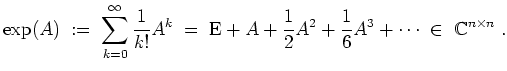
$ \mbox{$\displaystyle \exp(A) \; :=\; \sum_{k = 0}^\infty \frac{1}{k!} A^k \; ... ...\frac{1}{2} A^2 + \frac{1}{6} A^3 + \cdots \;\in\;\mathbb{C}^{n\times n}\; . $}$
Diese Reihe konvergiert eintragsweise für alle $ \mbox{$A\in\mathbb{C}^{n\times n}$}$ , und liefert wieder eine Matrix in $ \mbox{$\mathbb{C}^{n\times n}$}$ . Manchmal schreibt man auch $ \mbox{$e^A := \exp(A)$}$ .

Eigenschaften.

Sind $ \mbox{$A,\, B\,\in\,\mathbb{C}^{n\times n}$}$ , und ist $ \mbox{$AB = BA$}$ , so ist $ \mbox{$\exp(A+B) = \exp(A)\exp(B)$}$ .

Ist $ \mbox{$A\in\mathbb{C}^{n\times n}$}$ , und ist $ \mbox{$S\in\mathbb{C}^{n\times n}$}$ invertierbar, so ist $ \mbox{$\exp(S^{-1}AS) = S^{-1}\exp(A) S$}$ .

Sind $ \mbox{$A_i\in\mathbb{C}^{n_i\times n_i}$}$ für $ \mbox{$1\le i\le m$}$ , und für gewisse $ \mbox{$n_i\ge 1$}$ , so ist

$ \mbox{$\displaystyle \exp(\text{diag}(A_1,\dots,A_m)) \; =\; \text{diag}(\exp(A_1),\dots,\exp(A_m))\; , $}$
d.h. $ \mbox{$\exp$}$ für eine Blockdiagonalmatrix berechnet sich blockweise. Ferner ist $ \mbox{$\exp((z)) = (\exp(z))$}$ für $ \mbox{$(z)\in\mathbb{C}^{1\times 1}$}$ .

In der Regel stellt sich die Frage nach der Berechnung von $ \mbox{$\exp(tA)$}$ mit $ \mbox{$A\in\mathbb{C}^{n\times n}$}$ und einem Parameter $ \mbox{$t\in\mathbb{C}$}$ .

Einsetzen von Jordanblöcken.

Seien $ \mbox{$k\ge 1$}$ und $ \mbox{$\lambda\in\mathbb{C}$}$ gegeben. Wir erinnern an die Bezeichnungsweise

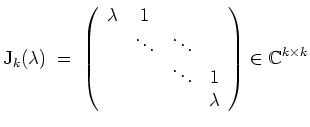
$ \mbox{$\displaystyle \text{J}_k(\lambda) \; =\; \left(\begin{array}{cccc} \... ...& \ddots & 1 \\ & & & \lambda \end{array}\right)\in\mathbb{C}^{k\times k} $}$
für einen Jordanblock der Kantenlänge $ \mbox{$k$}$ zum Eigenwert $ \mbox{$\lambda$}$ . Nicht erwähnte Einträge seien vereinbarungsgemäß gleich $ \mbox{$0$}$ .

Für $ \mbox{$t\in\mathbb{C}$}$ wird nun

$ \mbox{$\displaystyle \begin{array}{rcl} \exp(t\;\text{J}_k(\lambda)) &=& \ex... ...& & & & & 1 \\ \end{array}\right)\in\mathbb{C}^{k\times k} \; , \end{array}$}$
wobei $ \mbox{$\exp(t\lambda)$}$ einen skalaren Vorfaktor darstellt.

Berechnung von $ \mbox{$\exp(tA)$}$ allgemein.

Sei $ \mbox{$A\in\mathbb{C}^{n\times n}$}$ . Berechne die Jordanform von $ \mbox{$A$}$ in der Form

$ \mbox{$\displaystyle A \; =\; S\,\text{diag}\big(\text{J}_{n_1}(\lambda_1),\text{J}_{n_2}(\lambda_2),\dots,\text{J}_{n_m}(\lambda_m)\big)\, S^{-1} $}$
mit $ \mbox{$S\in\mathbb{C}^{n\times n}$}$ invertierbar, und den sich ergebenden $ \mbox{$n_i$}$ und $ \mbox{$\lambda_i$}$ für $ \mbox{$1\le i\le m$}$ . Für $ \mbox{$t\in\mathbb{C}$}$ ist dann
$ \mbox{$\displaystyle tA \; =\; S\,\text{diag}\big(t\;\text{J}_{n_1}(\lambda_1),t\;\text{J}_{n_2}(\lambda_2),\dots,t\;\text{J}_{n_m}(\lambda_m)\big)\,S^{-1} $}$
Mit obigen Regeln folgt
$ \mbox{$\displaystyle \exp(tA) \; =\; S\exp\big(\text{diag}\big(t\;\text{J}_{... ...}(\lambda_2)),\dots,\exp(t\;\text{J}_{n_m}(\lambda_m))\big)\big) S^{-1} \; , $}$
worin man nun die oben angegebene Formel für $ \mbox{$\exp(t\;\text{J}_{n_i}(\lambda_i))$}$ einsetzen kann.

Entsprechend ergibt sich $ \mbox{$\exp(A)$}$ im Spezialfall $ \mbox{$t = 1$}$ , sollte das einmal gefragt sein.